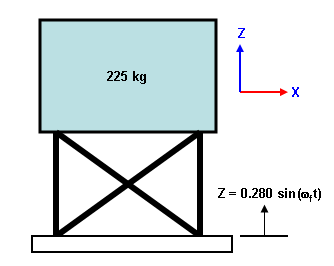
假设:具有移动式基座的柔性系统包含的主体质量为 225 kg、支撑结构刚度为 35000 N/m,阻尼因子为 0.188。基座以正弦曲线振动,系统固有频率下振幅为 0.280 cm。
|
物理装配件。 基座以结构固有率频振动。 |
|
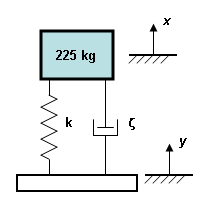
等效表示。 k = 35000 N/m ζ = 0.188 x 和 y 是在振动教科书中用于测量质量和基座的绝对运动的典型项。小写斜体项 x 和 y 表示位置与时间的函数。 |
查找:
- 质量位移相对于基座的大小。
- 质量位移的绝对大小(相对于静止源的位移)。
如果不想对整个支撑结构进行详细建模,可使用桁架单元表示。(请记住,桁架单元的刚度 k 为 A*E/L。)质量可以通过添加到桁架端点的集中质量表示。移动基座将通过固定边界条件表示,基础运动或基础加速度载荷将仿真基座的振动。带质量的桁架单元端点将有一个边界条件,用于限制质量仅在轴向振动。
步骤
- 执行“固有频率(模态)”分析,以获得固有频率。模态分析结果除了可提供频率之外(根据问题陈述的要求),还将用于以下两种分析类型。
- 执行基础加速度“频率响应”分析以获得质量的准稳态振幅。“频率响应”将仿真应用于模型的正弦载荷。
- 若要检查系统从无速度启动时出现的问题,请执行基础加速度“瞬态应力(模态叠加)”分析。“瞬态应力”使用用户定义的载荷曲线计算常规载荷的模型响应。瞬态期间会发生较大的变形吗?
构建模型:
- 启动新的 FEA 模型。
- 将分析类型设置为“线性: 固有频率(模态)”。
- 由于振动以厘米为单位,因此请为模型选择单位牛顿、厘米和秒。单击“替代默认单位”并将“单位制”下拉菜单设置为“自定义”,然后分别将力、长度和时间的对应单位设置为 N、cm 和 s。单击“确定”完成单位设置。
- 单击“新建”并输入模型名称。
- 通过“绘制”
 “绘制”
“绘制” “直线”添加一条直线来表示支撑结构。验证“作为构造体使用”复选框处于禁用状态。由于桁架单元是三维的,因此可采用任意方向,但出于一致性考虑,请使用上一图像中的方向。单元可采用任意长度(只要组合 A*E/L 得到的刚度值合适),请选择长度 2 cm。直线的起点为 (0,0,0),将下一个端点置于 (0,0,2) 处。关闭对话框。
“直线”添加一条直线来表示支撑结构。验证“作为构造体使用”复选框处于禁用状态。由于桁架单元是三维的,因此可采用任意方向,但出于一致性考虑,请使用上一图像中的方向。单元可采用任意长度(只要组合 A*E/L 得到的刚度值合适),请选择长度 2 cm。直线的起点为 (0,0,0),将下一个端点置于 (0,0,2) 处。关闭对话框。 - 使用“视图”
 “浏览”
“浏览” “封闭”封闭整个模型。
“封闭”封闭整个模型。 - 将“单元类型”设置为“桁架”。在树视图中的“单元类型”标题上单击鼠标右键,然后选择“桁架”。
- 使用“单元定义”设置桁架属性。在“单元定义”标题上单击鼠标右键,然后选择“编辑单元定义”。可以将“横截面面积”设置为任何值,请输入值 1 cm 2 ,然后单击“确定”。
- 为简化输入,尤其是涉及质量的项,请将“显示单位”定义 kg 以作为质量单位。
- 在靠近树视图顶部的“单位制”分支上单击鼠标右键,然后选择“新建”。
- 将“单位制”下拉菜单设置为“自定义”,然后分别将力、长度、时间和质量的对应单位设置为 N、cm、s 和 kg。
- 为方便起见,请输入“说明”,例如 N cm kg。
- 单击“确定”完成设置并激活“显示单位”。
- 输入材料属性。在树视图中的“材料”标题上单击鼠标右键,然后选择“编辑材料”命令。由于已设定单元的长度和横截面面积,因此无法随意选择材料属性。弹性模量必须为 700 N/cm 2 以获得合适的刚度。[k = 35000 N/m = 350 N/cm = A*E/L = (1 cm 2 )*(700 N/cm 2 )/(2 cm)]。选择条目“[自定义]”,然后单击“编辑属性”。为“弹性模量”输入 700 N/cm 2 以避免因单元质量为 0 导致的潜在求解困难,为“质量密度”输入 0.05 kg/cm 3 。这样一来,根据之前选择的长度和面积,该单元的总质量将为 1 kg,与应用的质量 225 kg 相比变得无关紧要。单击“确定”两次以完成属性设置。
- 为模型添加边界条件。选择位于弹簧底部的顶点(“选择”
 “形状”
“形状” “点或矩形”和“选择”
“点或矩形”和“选择” “选择”
“选择” “顶点”),单击鼠标右键,然后选择“添加”
“顶点”),单击鼠标右键,然后选择“添加” “节点边界条件”。单击“无平动”在 X、Y 和 Z 平动(Tx、Ty、Tz)方向上固定节点。单击“确定”以应用边界条件。(由于桁架单元没有转动自由度,因此“固定”边界条件在此情况中也适用)。
“节点边界条件”。单击“无平动”在 X、Y 和 Z 平动(Tx、Ty、Tz)方向上固定节点。单击“确定”以应用边界条件。(由于桁架单元没有转动自由度,因此“固定”边界条件在此情况中也适用)。 - 选择位于弹簧顶部的顶点(“选择”
 “形状”
“形状” “点或矩形”和“选择”
“点或矩形”和“选择” “选择”
“选择” “顶点”),单击鼠标右键,然后选择“添加”
“顶点”),单击鼠标右键,然后选择“添加” “节点边界条件”。弹簧可以在轴向 (Z) 上自由移动,但不可以偏离该轴。激活 Tx 和 Ty 的复选框。单击“确定”以应用边界条件。
“节点边界条件”。弹簧可以在轴向 (Z) 上自由移动,但不可以偏离该轴。激活 Tx 和 Ty 的复选框。单击“确定”以应用边界条件。 - 在顶部顶点仍处于选定状态下,添加结构的质量。单击鼠标右键,然后选择“添加”
 “节点集中质量”。请确保“质量单位”选项处于选中状态,并输入值 225 作为“X 方向”质量(单位为千克)。(应选中“均布”复选框以使质量在所有三个方向上平等作用。)单击“确定”应用集中质量。
“节点集中质量”。请确保“质量单位”选项处于选中状态,并输入值 225 作为“X 方向”质量(单位为千克)。(应选中“均布”复选框以使质量在所有三个方向上平等作用。)单击“确定”应用集中质量。 - 如图所示,模型仅有一个只能在一个方向(Z 平动)上移动的节点,此时存在一个自由度。暂时不再往下探讨,此模型太小而无法在 FEA 中求解!模型需要更多自由度(或方程)才能进行求解。因此,请选择直线(“选择”
 “形状”
“形状” “点 或矩形”和“选择”
“点 或矩形”和“选择” “选择”
“选择” “直线”),然后将其分割为四个部分(“绘制”
“直线”),然后将其分割为四个部分(“绘制” “修改”
“修改” “分割”
“分割” 4
4 “确定”)。这将创建三个新节点以供求解器使用,接下来需要约束这些新节点使其仅在轴向移动。在顶点周围拖出一个框将其选中(“选择”
“确定”)。这将创建三个新节点以供求解器使用,接下来需要约束这些新节点使其仅在轴向移动。在顶点周围拖出一个框将其选中(“选择” “形状”
“形状” “矩形”和“选择”
“矩形”和“选择” “选择”
“选择” “节点”),单击鼠标右键,然后选择“添加”
“节点”),单击鼠标右键,然后选择“添加” “节点边界条件”。请注意,对话框窗口的标题栏指示正在创建三个节点边界条件对象。选中 Tx 和 Ty 复选框。单击“确定”以应用边界条件。
“节点边界条件”。请注意,对话框窗口的标题栏指示正在创建三个节点边界条件对象。选中 Tx 和 Ty 复选框。单击“确定”以应用边界条件。
- 运行模态分析前的最后一步是为模式数和频率数设置分析参数。选择“设置”
 “模型设置”
“模型设置” “参数”,然后为“要计算的频率/模式数”输入 1。单击“确定”。(由于创建的模型具有 1 个自由度,因此仅需计算一个频率。)
“参数”,然后为“要计算的频率/模式数”输入 1。单击“确定”。(由于创建的模型具有 1 个自由度,因此仅需计算一个频率。)
步骤 1:执行固有频率分析
- 使用“分析”
 “分析”
“分析” “运行仿真”命令运行分析。分析完成后,该模型将显示在“结果”环境中。请记住固有频率为 1.985 个周期/秒。
“运行仿真”命令运行分析。分析完成后,该模型将显示在“结果”环境中。请记住固有频率为 1.985 个周期/秒。
步骤 2:执行频率响应分析
- 返回“FEA 编辑器”选项卡。
- 若要计算因基座振动产生的稳态变形,请将“分析类型”设置为“频率响应”(“分析”
 “更改”
“更改” “类型”
“类型” “线性”
“线性” “频率响应”)。当系统提示将模型复制到新设计工况时,请单击“是”。固有频率结果将包含在“设计工况 1”中,频率响应结果将包含在“设计工况 2”中,可通过选择设计工况快速访问这两个结果。
“频率响应”)。当系统提示将模型复制到新设计工况时,请单击“是”。固有频率结果将包含在“设计工况 1”中,频率响应结果将包含在“设计工况 2”中,可通过选择设计工况快速访问这两个结果。 - 对于此分析类型,所有输入均通过“分析参数”输入。选择“设置”
 “模型设置”
“模型设置” “参数”,然后单击“分析设置”。(“输出控件”下的选项仅用于获取其他文本类输出,因此通常不需要激活这些选项。)在四个选项卡中输入载荷的完整定义。各个选项卡中的输入可总结如下:
“参数”,然后单击“分析设置”。(“输出控件”下的选项仅用于获取其他文本类输出,因此通常不需要激活这些选项。)在四个选项卡中输入载荷的完整定义。各个选项卡中的输入可总结如下: - 可在“激励节点”选项卡中指定一个或多个载荷的位置,但载荷频率和振幅不在此选项卡上指定,而是通过指定“激励频率定义索引”将位置链接到受迫振动频率。(在某些情况下,最好先填写其他选项卡,最后填写“激励节点”选项卡。)
- 激励频率将在“激励频率”选项卡中指定,但是载荷的振幅不在此选项卡上指定。因此,如果近似处理正弦扫描测试,则需要在此选项卡上输入具有不同受迫振动频率(从最小频率到最大频率,步长 f)的多个行。
- 模型的阻尼在“阻尼比”选项卡中输入。此表将在每个激励频率处插值,以确定每个受迫振动频率处的阻尼比。因此,此表中的频率不需要复制激励频率表,但是需要覆盖整个激励频率范围。
- 应用载荷的振幅在“振幅”选项卡中输入。此表将在每个激励频率处插值,以确定每个受迫振动频率处的正弦载荷振幅。因此,此表中的频率不需要复制激励频率表,但是需要覆盖整个激励频率范围。
- 由于“频率响应”分析使用模态分析中的结果,因此请在“使用设计场景中的模态结果”字段中输入 1。
- “激励节点”选项卡用于定义模型中存在正弦载荷的位置。为此示例设置以下值:
- 在“节点编号”部分中选择选项“基础加速度运动”以指明将振动基座支架。
- 由于载荷将为基础加速度,因此“激励类型”必须为“加速度输入”,而不是“力输入”。
- 在“激励的方向”部分中选择选项“Z 方向”作为基座的振动方向。模型中被限制在 Z 方向上的节点将被视为与基座相连,从而将一起进行振动。
- 为“振幅比例因子”输入 1。此值用于缩放应用载荷。
- “激励频率”选项卡用于定义模型的振动频率。对于此示例,只需在表中输入一个频率:1.985 Hz。
- “阻尼比”选项卡用于定义阻尼比与频率的函数关系。如果仅在表中输入一行,则所有受迫振动频率的阻尼将相同。因此,分别输入 1 Hz 和 0.188 作为频率和阻尼比(根据问题陈述中给出内容)。
- “振幅”选项卡用于定义应用载荷的振幅(加速度或力)与频率的函数关系。此模型使用基础加速度,而问题陈述会给出基础运动的振幅。因此,要获得加速度,只需利用位移的二阶导数 (y = 0.280*sin(ωt)) 得到加速度方程 (ay = -0.280*ω2*sin(ωt)) 即可。因此,计算得出的加速度大小 = (0.280 cm)*[(1.985 个周期/秒)*(2*pi 弧度/周期)]2 = 43.55 cm/s2。该界面使用的加速度单位为 G,因此用加速度大小除以重力常数即得到 (43.55 cm/s2)/(981 cm/s2) = 0.0444 G。对于所有应用频率范围内的恒定载荷,请输入一行,如 “频率”= 1 和“加速度”= 0.0444。(由于未向模型施加任何力,因此可留空“力”列。)
- 单击“确定”两次以应用分析参数。
- 使用“分析”
 “分析”
“分析” “运行仿真”命令运行分析。分析完成后,该模型将显示在“结果”环境中。
“运行仿真”命令运行分析。分析完成后,该模型将显示在“结果”环境中。 - 给出的位移结果是相对位移。(注意基座的位移显示为 0,而不是输入的振幅 0.280 cm。)由于模型在除 Z 方向之外的所有方向上均受到约束,因此位移大小结果值与 Z 位移结果相同,但出于演示目的,最好查看 Z 位移结果。请使用“结果等值线”
 “位移”
“位移” Z 命令。
Z 命令。 - “频率响应”分析结果针对相内、相外和 SRSS 结果给出。使用“结果选项”
 “具体分析”
“具体分析” “响应类型”下拉菜单查看每种类型。由于在此示例中相内分量几乎为零,因此相外和 SRSS 相同。质量相对于基座最多移动 0.745 cm。
“响应类型”下拉菜单查看每种类型。由于在此示例中相内分量几乎为零,因此相外和 SRSS 相同。质量相对于基座最多移动 0.745 cm。 - 可如下计算质量的绝对位移。(请参见图 1 中的项。x、y、z 是时间为 t 时的绝对位置,X、Y、Z 是整个周期内的最大值或最大振幅。)
Relative displacement z = x - y Absolute displacement x = z + y The motion of the base is given as y = Y*sin(ωt) and the relative displacement z = Z*sin(ωt-φ), where φ is the phase angle. Thus, x = Z*sin(ωt-φ) + Y*sin(ωt)
在“频率响应”总结文件(可通过“报告”环境访问)中,计算得出的相位角应为 90 度(请参见下文),因此
x = Z*sin(ωt-φ) + Y*sin(ωt) = Z*sin(ωt-90) + Y*sin(ωt) = -Z*cos(ωt) + Y*sin(ωt)
由于存在相位差,因此 x 的最大位移(表示为 X)不等于 Y + Z。但是,可以看出最后一个方程的替换形式为 x = X*sin(ωt + φ),其中值 X = sqrt(Z2 + Y2),φ 为相位角。因此,当 Z = 0.745 cm 且 Y = 0.280 cm 时,质量的绝对位移为 0.796 cm。
“频率响应”总结文件中的摘录:
START OF LOAD 1 Applied frequency case # 1 (Applied frequency = 1.985E+00 Hx) Mode No. Phase Angel (Deg.) Amplitude 1 8.9934E+01 1.1172E+00
步骤 3:执行“时间历史记录”分析:
- 返回“FEA 编辑器”选项卡(“工具”
 “环境”
“环境” “FEA 编辑器”)。
“FEA 编辑器”)。 - 若要计算因基座振动产生的瞬态变形,请将“分析类型”设置为“瞬态应力”(“分析”
 “更改”
“更改” “类型”
“类型” “线性”
“线性” “瞬态应力(模态叠加)”)。当系统提示将模型复制到新设计工况时,请单击“是”。因此,瞬态应力结果将包含在“设计工况 3”中。
“瞬态应力(模态叠加)”)。当系统提示将模型复制到新设计工况时,请单击“是”。因此,瞬态应力结果将包含在“设计工况 3”中。 - 与之前一样,请在“分析参数”下定义基础运动(
“设置”
 “模型设置”
“模型设置” “参数”
)。
“参数”
)。 - 从静止状态变为准稳态条件需要的周期数是未知的。如果假设将需要 10 个周期,则 5 秒的持续时间应该足够。[= (10 个周期)/(2 个周期/秒)]。若要在一个正弦周期内准确捕获结果,请尝试将周期分割成 50 步。这样每个时间步的大小为 1/[(2 个周期/秒)*(50 步/周期)] = 0.01 秒。输入 500 作为“时间步数”,0.01 作为“时间步大小”。
- 定义基础运动的载荷曲线;单击“载荷曲线”。需要填充“时间”和“因子”的载荷曲线表,其中因子是基础加速度(以 cm/s2 为单位)。在之前的计算中,基础加速度大小为 43.55 cm/s2,因此基础加速度的方程为 (43.55 cm/s2)*sin(1.985 Hz * (2pi 弧度/周期) * 时间)。如果不想为每个时间步键入值,则可以使用电子表格执行计算,然后将其保存为逗号分隔值 (CSV) 文件,并将其导入载荷曲线。此方法用于创建位于 Autodesk Simulation 安装文件夹的“模型”子文件夹下的文件。因此在“载荷曲线输入”对话框中单击“导入”。单击“浏览”,选择文件 43.55sine.csv,然后单击“打开”。随即显示文件内容。由于第一行是用于标识数据的标签,因此输入 1 作为“跳过前 _ 行”的值。单击“导入”完成该过程。随即将显示正弦荷载曲线。单击“确定”关闭“载荷曲线输入”对话框。
- 按照问题陈述输入 0.188 作为“阻尼系数(临界分数)”。
- 由于此示例使用基础加速度,因此可以忽略“载荷”选项卡(用于应用节点载荷),而在“选项”选项卡中,将“地面运动类型”设置为“平动”。
- 单击“设置”指定基础运动的参数。即将“Z 方向”的“载荷曲线”设置为“载荷曲线 1”,并将“加速度大小”设置为 1 cm/s2。(之所以将加速度大小设置为 1 是因为载荷曲线会给出完整幅值。)单击“确定”,关闭“基础运动设置”对话框。
- 由于“瞬态应力”分析使用模态分析中的结果,因此请在“使用设计场景中的模态结果”字段中输入 1。
- 单击“确定”,关闭“分析参数”,模型即已准备就绪可进行分析。单击“分析”
 “分析”
“分析” “运行仿真”。
“运行仿真”。 - 分析完成后,该模型将显示在“结果”环境中。注意结果的 500 个时间步可供查看:一个时间步对应于一个计算步骤。若不想一次查看一个时间步结果,则可以绘制结果。
- 请将“结果类型”设置为“Z 位移”(“结果等值线”
 “位移”
“位移” Z)。
Z)。 - 选择集中质量处的节点(“选择”
 “形状”
“形状” “点或矩形”和“选择”
“点或矩形”和“选择” “选择”
“选择” “节点”,然后单击模型顶部的节点)。单击鼠标右键,然后选择“图形表示值”。此时将另外创建一个带图形的演示窗口。结果应类似于图 2。在大约 5 个周期后达到准稳态条件。直观结果显示相对于支架的质量预期位移大约为 0.75 cm。
“节点”,然后单击模型顶部的节点)。单击鼠标右键,然后选择“图形表示值”。此时将另外创建一个带图形的演示窗口。结果应类似于图 2。在大约 5 个周期后达到准稳态条件。直观结果显示相对于支架的质量预期位移大约为 0.75 cm。 - 通过在树视图中单击等值线窗口“演示 1 <未命名>”返回该窗口。接近 4 秒的时间步应接近最大位移,可以以此着手检查位移的实际值。使用“结果等值线”
 “荷载工况选项”
“荷载工况选项” “载荷工况”
“载荷工况” “设置”并输入值 400,然后单击“确定”。前进或后退几个时间步(“结果等值线”
“设置”并输入值 400,然后单击“确定”。前进或后退几个时间步(“结果等值线” “荷载工况选项”
“荷载工况选项” “下一个”或“上一个”),直到找到具有最大位移的时间步。时间步 403 的位移为 0.742 cm。
“下一个”或“上一个”),直到找到具有最大位移的时间步。时间步 403 的位移为 0.742 cm。
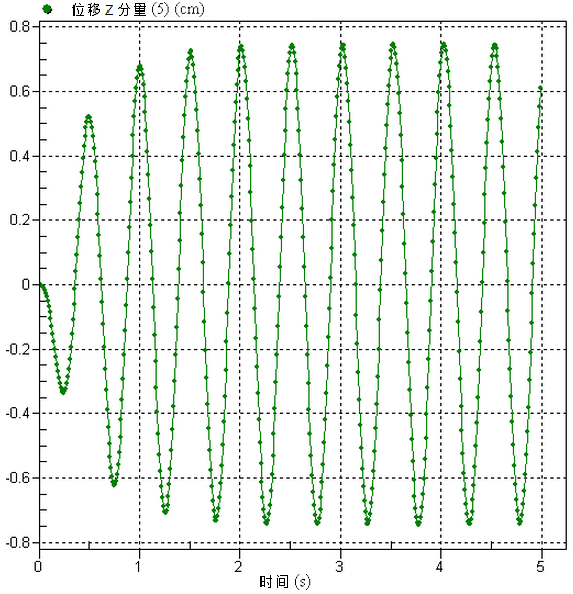
图 2:质量的位移图。
模型和结果存档 (ground motion.ach) 位于 Autodesk Simulation 安装目录的“模型”子文件夹中。
此示例可以使用许多振动教科书中的方法求解。此特定示例排列在《振动分析》(作者 Vierck, Robert K.,出版社 Harper & Row)第二版的第 129-130 页中的示例 4-9 之后。