此页面上的信息适用于以下分析类型（除非注明）：
机械运动仿真 (MES)
非线性材料模型静态应力
在机械运动仿真分析和非线性材料静态应力分析中，大部分载荷跟随载荷曲线。在“分析参数”对话框的“载荷曲线”选项卡中定义载荷曲线。可以在此处输入任何形状的曲线。
选择“添加下一条载荷曲线”或“添加载荷曲线”按钮以添加其他载荷曲线。您可以具有跟随不同载荷曲线的不同载荷。例如，在整个分析中重力可以是常数，因此将其指定给一条载荷曲线。力可能会按正弦规律变化以对偏心旋转进行仿真，因此将其指定给不同的载荷曲线。
在“所选载荷曲线的数据”部分中通过一组点定义载荷曲线，其通过一系列直线段理想化真实曲线。第一列为时间或结果（请参见下文的详细信息），其余列调整指定给载荷曲线的载荷（通常通过乘以载荷）。（激励器单元和规定位移将载荷曲线乘子用作长度或转动变化，而不是乘数。）根据需要将线性插入载荷曲线以在相应的时间或结果处确定乘子。
根据需要使用“添加行”按钮在载荷曲线上定义多个点，或使用“删除行”按钮删除当前行。需要按时间或结果的升序顺序输入载荷曲线数据点；如果未以此方式输入数据，则使用“排序”按钮。
您还可以使用“导入载荷曲线”按钮导入载荷曲线。首先，以逗号分隔文件 (.csv) 格式创建一个文本文件，其中文本文件的每行对应一行载荷曲线，并用逗号分隔载荷曲线的每列的行上的每个值。（文本文件中不包含载荷曲线的“索引”列。）
- 目标载荷曲线应与 CSV 文件具有相同的列数。例如，如果为基于结果的载荷曲线使用具有 4 列的 CSV 文件，请根据需要使用“添加载荷曲线”和“添加列”按钮创建一个具有 4 列的空白载荷曲线表。
- 逗号分隔文件中的值通过使用活动的“显示单位”导入。导入数据之前，您可根据需要更改“显示单位”。例如，如果“显示单位”设置为秒，则将值 3.14 作为 3.14 秒导入，如果“显示单位”设置为分钟，则作为 3.14 分钟导入。
基于时间的载荷曲线
当载荷作为时间函数变化时，在“所选载荷曲线的数据”部分中选择“时间”。然后，载荷曲线具有两列：“时间”和“乘子 1”。将载荷曲线的数据点直接输入到“载荷曲线”电子表格中，或导入载荷曲线（请参见上文）。
请注意，载荷曲线的“时间”列基于活动的“显示单位”转换。
当接近带有一系列直线段的高阶曲线时，载荷曲线中点的间距应小于分析中遇到的最小时间步。例如，假设一台以已知速度加速的滑道起重机。这通过在车轮位置应用规定位移进行仿真，其中位移与时间为 d = 0.5*a*t^2。如果根据捕获率以时间步 t 计算并输入载荷曲线，则只要在分析中不会缩减时间步，就会精确跟随曲线。只要自动缩减时间步以收敛求解，就会立即插入载荷曲线。发生这种情况时，规定位移不会跟随精确的加速度方程。请参见图 1。
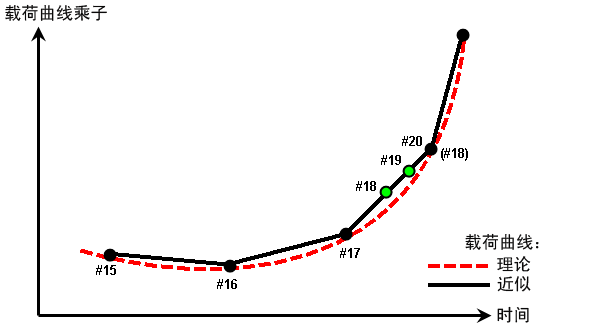
图 1：部分载荷曲线
时间步 #15、#16 和 #17 跟随理论曲线。如果时间步 #18 能够收敛，载荷将仍在理论曲线上 (#18）。但当时间步缩减时，时间步 #18 和 #19 会被插入，因此这会导致稍有不同的载荷。在许多情况下，都会忽略差异（尤其是考虑通常由 FEA 生成的近似值）。
基于结果的载荷曲线
想象一下开关装配件中的磁性接触。磁性吸引力不是已知的时间函数，因为接触位移（由于分析中的其他载荷）与时间是未知的。磁力会根据部件之间的分离而变化。在这种情况下，将载荷曲线定义为结果函数，并且分析将会在整个时间内相应地改变载荷。
在访问“分析参数”对话框以定义基于结果的载荷曲线之前，将探测添加到模型中。探测位于模型中将在载荷曲线中使用其结果的位置。若要添加探测，选择一个或多个顶点（“选择”
“选择”“顶点”），单击鼠标右键，然后选择“添加”“节点探测”。随即显示一个对话框，可以在其中为节点探测对象输入说明。（请参见“载荷和约束：探测”页面。）
若要将载荷曲线设置为基于结果，请选择“所选载荷曲线的数据”中的“查询值”。然后，载荷曲线将从下面两列开始：“查询”和“乘子 1”。（可以按如下所示添加其他列。）查询值使用“定义/编辑查询值”按钮定义。定义后，可以使用“查询值”下拉菜单定义查询值。查询值的名称将变为载荷曲线电子表格的第一列的标题。
- 规定位移和激励器单元无法使用基于结果的载荷曲线。
- 查询载荷曲线的第一列（包含查询值方程的结果）未基于活动的“显示单位”转换。查询值和第一列的单位基于“模型单位”。
定义和编辑查询值
单击“定义/编辑查询值”按钮将显示“定义查询值”对话框，在这里会基于给定位置的结果定义查询值。“定义查询值”对话框中的函数如下所示，按照它们正常使用的顺序列出。
- 单击“添加”按钮可定义新的查询值。创建的查询值的名称必须唯一，但不能包含任何空格。“时间”也是一个不可接受的名称，以免与分析时间产生混淆。
- 使用“查询值名称”下拉菜单查看针对之前定义的任何名称的输入。输入显示之后，任何输入均可更改，并且当切换到其他查询值或是单击“确定”按钮关闭对话框时，输入将会保存。
- 单击“添加行”按钮向变量电子表格添加其他行。在电子表格中定义的变量用于定义哪个结果与查询值关联的方程。添加的每个变量都会自动被赋予名称 V1、V2 等。通过在电子表格中单击变量的名称，可以将其更改为更具描述性的名称。
- 在电子表格中，使用下拉菜单为每个变量选择一个探测和一个结果。只有添加到模型的探测才可用于变量定义。可在探测处使用的结果如下所示：
- X 位移
- Y 位移
- Z 位移
- X 速度
- Y 速度
- Z 速度
- “方程”文本框是将电子表格中描述的变量组合起来以定义查询值名称的位置。（其他查询值不能包含在方程中）。例如，如果结果如同节点的 Y 位移这么简单，则方程将为 V1，其中 V1 被定义为相关探测处的 Y 位移。如果查询值名称需要是三个节点的平均值，则方程将为 (V1+V2+V3)/3。方程中可使用以下运算符：
运算符 说明 （和） 用来对操作进行分组的圆括号。 ** 或 ^ 指数函数，或求解一个数的幂次方。例如，V1^2 将计算出变量 V1 的平方。 * 相乘。 / 相除。 + 相加。 - 减或表示数字的负值，例如 V1-V2 或 -V1*5。 cos( ) 括号内的值的余弦。该值必须以弧度为单位。 sin( ) 括号内的值的正弦。该值必须以弧度为单位。 tan( ) 括号内的值的正切。该值必须以弧度为单位。 exp( ) 括号内的值的自然指数函数（以 e 为底数的幂），如 eV1。 log( ) 括号内的值的自然对数，或以 e 为底数的对数，在数学中通常写为 ln( )。 abs( ) 括号内的值的绝对值。 sqrt( ) 括号内的值的平方根。 acos( ) 括号内的值的反余弦函数，即反余弦。 asin( ) 括号内的值的反正弦函数，即反正弦。 atan( ) 括号内的值的反正切函数，即反正切。 cosh( ) 括号内的值的双曲余弦。 sinh( ) 括号内的值的双曲正弦。 tanh( ) 括号内的值的双曲正切。 log10( ) 括号内的值的以 10 为底的对数，通常以 log( ) 的算术式书写。
条件语句和多个载荷曲线乘子
如到目前为止所述，为载荷曲线选择的查询值将成为用于确定乘子的单个值 – 就像时间是基于时间的载荷曲线中用于确定载荷乘子的单个值一样。在某些情况下，多个结果或多个查询值会影响载荷的大小。在这些情况下，将结合使用“条件”文本框和电子表格中的多个列，以根据选定的查询值确定对哪个乘子列进行插值。
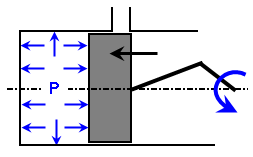
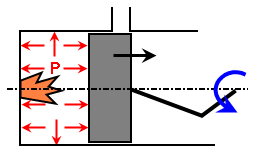
例如，假设一台两冲程引擎，示意图如图 2 所示。请注意，图 2a 中的活塞位置与图 2b 中相同。但是，图 2a 中的压力基于供给压力以及活塞自排气口关闭（气体压缩）后的运动，而图 2b 中的压力则基于燃烧压力以及活塞在燃烧（气体膨胀）后的运动。因此，载荷曲线不能基于活塞的位置，而是可以基于活塞的位置以及速度。这种类型的控制是通过使用“条件”文本框获得的。格式如下所示：
IF（查询值测试比较; True 时的乘子列; False 时的乘子列）
其中
- “查询值”是现有查询值名称，使用“定义/编辑查询值”创建和定义。
- “测试”是以下条件符号之一：
符号 说明 >= 或 => 大于或等于 <= 或 =< 小于或等于 = 等于 > 大于 < 小于 - 比较是一个数值。它不能是另一个查询值。因此，要使用查询值，如 Vel1 > Vel2，请定义一个新的查询值 Vel3 = Vel1 – Vel2，然后使用比较测试 Vel3 > 0。
- “True 时的乘子列”是一个数字，表示比较测试为 True 时载荷曲线中使用哪个乘子列
- “False 时的乘子列”是一个数字，表示比较测试为 False 时载荷曲线中使用哪个乘子列
请注意，分号 (;) 用于分隔 IF 条件的三个部分。
|
(a) 供给气体被压缩。 |
(b) 燃烧气体膨胀。 |
|
图 2：两冲程活塞 尽管活塞位置对于这两个位置都是相同的，但压力 P 不同。 |
|
根据条件测试的结果，将对载荷曲线电子表格中相应的列进行插值。可以使用“添加列”和“删除列”按钮来向电子表格中添加乘子列或从电子表格中删除乘子列。如果没有使用条件语句（“条件”文本框为空），则无论在电子表格中输入了多少列，都将仅使用“乘子 1”列。
- 条件方程可以嵌套，以便可以包括“与”类型运算。例如，我们来分析语句 IF(sep1<10;3;IF(vel>0;1;2))。如果由变量 sep1 定义的结果小于 10，则使用乘子列 3（True 条件）。如果 sep1 不小于 10（False 条件），则 False 条件的乘子列是另一个需要求值的测试 - 如果由变量 vel 定义的结果大于 0，则使用乘子列 1 中的乘子；如果 vel 不大于 0，则使用乘子列 2。总之，
- 如果 sep1 小于 10，则使用乘子列 3。
- 如果 sep 1 大于或等于 10，并且如果 vel 大于 0，则使用乘子列 1。
- 如果 sep1 大于或等于 10，并且如果 vel 小于或等于 0，则使用乘子列 2。
示例 1：磁力
对于图 3 中所示的磁力示例，假设以下参数：
- X = 0.5 英寸的静止位置（激活磁体之前）
- 激活磁体之后，F = 0.3125/(S^2)，其中 S 是实际分离
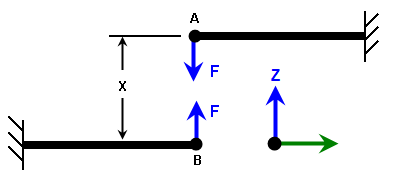
图 3：磁吸引力示例
特定于磁力设置的步骤如下所示：
- 选择顶部节点 A（“选择”“选择”“顶点”），然后应用节点力（右键单击“添加”“节点力”）。将力的值设置为 -1，将方向设置为 Z 方向。通过使用单位力，载荷曲线乘子将是总磁力。单击“确定”按钮应用力。
- 在“节点”仍处于选中状态情况下，添加探测（单击鼠标右键）。输入“顶部节点”的说明，然后单击“确定”按钮。
- 选择底部节点 B（“选择”“选择”“顶点”），然后应用节点力（右键单击“添加”“节点力”）。将力的值设置为 +1，将方向设置为 Z 方向。单击“确定”按钮应用力。
- 在“节点”仍处于选中状态情况下，添加探测（右键单击“添加”“节点探测”）。输入底部节点的说明，然后单击“确定”按钮。
- 访问“分析参数”对话框（“分析: 参数”）并选择单选按钮以将载荷曲线类型设置为“查询值”。载荷曲线电子表格的第一列从“时间”更改为“查询值”。
- 定义代表两个磁体之间计算的分离的新变量。单击“定义/编辑查询值”按钮。这将打开一个新对话框。单击“添加”按钮并输入新变量名称 Separat on。单击“确定”按钮完成查询值名称的输入并返回到“定义查询值”对话框。
- 分离是一个基于两个节点的位移的方程，因此请单击“添加行”按钮一次，以将第二个变量 V2 添加到电子表格。
- 对于变量 V1，选择“Z 位移”的探测“顶部节点”和结果。
- 对于变量 V2，选择“Z 位移”的探测“底部节点”和结果。
- 然后，在“方程”文本框中输入计算的分离的方程。键入 0.5+V1-V2。请注意，顶部节点的正向位移将增大分离；因此将向初始分离 0.5 增加 V1。底部节点的正向位移将减小分离；因此将从初始分离 0.5 减去 V2。
- 单击“确定”按钮关闭“定义查询值”对话框。
- 返回“分析参数”主对话框，使用“查询值”下拉框，并选择“分离”作为查询值。载荷曲线电子表格的第一列从“查询值”更改为“分离”。
- 最后，根据各个分离的乘子（此设置中为磁力）求值，然后将它们输入到载荷曲线电子表格中。尽管当分离为 0 时力理论上为无限大，但从 FEA 角度来看，以下载荷曲线更实际（这里需要接触以防部件彼此穿过，因此分离的值不得达到 0）。请注意，其他大于 0.5（初始分离）的分离条目。如果项目振动或其他载荷导致它们进一步远离初始分离，则需要载荷曲线涵盖所有可能的分离范围。
索引 分离 乘子 1 1 0 100 2 0.1 31.25 3 0.2 7.81 4 0.3 3.47 5 0.4 1.95 6 0.5 1.25 7 0.6 0.868 8 0.7 0.638 9 0.8 0.488 - 单击“查看图形”按钮以确认形状为预期的双曲线。看起来好像 0 和 0.2 之间需要多个数据点才能生成更平滑的曲线。
示例 2：两冲程活塞
对于图 2 和 4 中显示的两冲程活塞，假设以下（虚构）参数：
- X = -1.25 英寸（当排气口完全堵住时活塞的 X 位移）
- 压缩冲程 = 1.5 英寸 (X0 = -1.5)
- 缸径 = 3 英寸直径
- V0 = 14.2 英寸^3 = 排气口堵上时滞留空气的量
- 送风压力 = 10 psig
- 燃烧压力 = 1000 psig
- 每个阶段都是一个等温过程；可以根据理想的气体定律计算气体压力。
- 从活塞从 X0 移动的距离开始粗略估计活塞和气缸盖之间滞留的空气量。本讨论中忽视由于缸径膨胀导致的空气量变化。
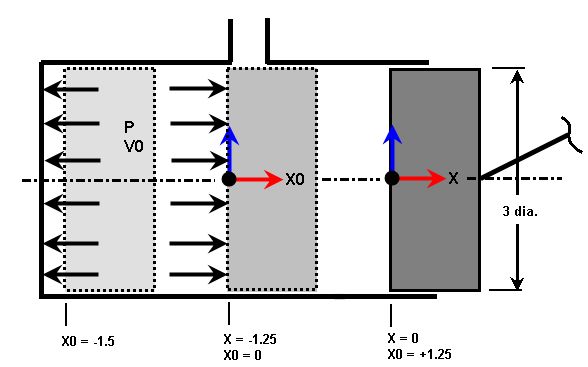
图 4：两冲程活塞示例
活塞显示在三个位置。X=0 是绘制模型的位置，X0=0 是排气口堵塞的位置，因此滞留的气体量为 V0 和压力为 P，X0=-1.5 为活塞的向前位置。
当然，为了将可压缩性和热损失考虑在内，载荷曲线中施加的压力可能比理想气体定律更复杂。此外，该评论仅包括气缸盖和活塞盲边上的压力。需要其他工作以包含气缸壁侧面和活塞杆端的压力；这些压力跟随不同的基于结果的载荷曲线。
- 在活塞的盲端和气缸盖上选择表面（“选择”“选择”“表面”），然后施加 1 psi 的单位压力（单击鼠标右键并选择“添加”“表面压力/面力”）。选中“随动”复选框，然后单击“确定”按钮以施加压力。
- 忽略气缸盖的变形，可以仅根据活塞的位置计算滞留的空气量。在活塞上选择一个节点（“选择”“选择”“顶点”），单击鼠标右键，然后选择“添加: 节点探测”。输入活塞的描述并单击“确定”添加探测。
- 访问“分析参数”对话框（“分析: 参数”）并选择单选按钮以将载荷曲线类型设置为“查询值”。载荷曲线电子表格的第一列从“时间”更改为“查询值”。
- 定义一个代表活塞相对于排气口位置的新变量（或图 4 中的位置 X0）。单击“定义/编辑查询值”按钮。这将打开一个新对话框。单击“添加”按钮并输入新变量名称 X0。单击“确定”按钮完成查询值名称的输入并返回到“定义查询值”对话框。
- 对于变量 V1，选择“X 位移”的探测“活塞”和结果。
- 然后，在“方程”文本框中输入相对于排气口 X0 的活塞位置的方程。键入 V1+1.25。
- 定义一个代表活塞速度的新变量。单击“添加”按钮并输入新变量名称“Velocity”。单击“确定”按钮完成查询值名称的输入并返回到“定义查询值”对话框。
- 对于变量 V1，选择“X 速度”的探测“活塞”和结果。请注意，同一探测是如何用于多个查询值的。此外，查询值 X0 中的变量 V1 完全独立于查询变量“Velocity”中的变量 V1。
- 活塞速度的方程只是变量 V1。在“方程”文本框中键入 V1，单击“确定”按钮关闭“定义查询值”对话框。
- 返回“分析参数”主对话框，使用“查询值”下拉框，并选择“X0”作为查询值。载荷曲线电子表格的第一列从“查询值”更改为“X0”。
- 此分析中需要基于速度的条件，如先前所述。在“条件”文本框中输入文本“IF(Velocity>0;1;2)”。当速度为正（活塞移至右侧）时，燃烧气体膨胀，并且将使用乘子列 1。当速度为负（活塞移至左侧）时，供给气体被压缩，并且将使用乘子列 2。
- 单击“添加列”按钮将第二个乘子列添加到载荷曲线电子表格中。
- 最后，根据各个活塞位置的乘子（此设置中为压力）进行求值，然后将它们输入到载荷曲线中。使用“理想气体定律”，可根据初始压力 Psupply 和气体量 Vinitial 计算压缩冲程 (-1.5<=X0<=0) 的压力 Pc，如下所示：
Pinitial*Vinitial = P*V
Psupply*V0 = P*(V0+X0*(pi/4)*缸径^2)
(10 psig + 14.7 psi)*(14.2 英寸^3) = (Pc+14.7 psi)*(14.2 英寸^3+7.0686*X0)
Pc = 350.74/(14.2+7.0686*X0) - 14.7
对于膨胀冲程，可根据以下方程计算表压 Pe
Pinitial*Vinitial = P*V
Pcombustion*(V0 - (冲程)*(pi/4)*缸径^2) = P*(V0+X0*(pi/4)*缸径^2)
(1000 psig + 14.7 psi)*(14.2 英寸^3-10.60 英寸^3) = (Pe+14.7 psi)*(14.2 英寸^3+7.0686*X0)
Pe = 3652.92/(14.2+7.0686*X0) - 14.7
索引 X0 乘子 1
（气体膨胀，Pe）
乘子 2
（气体压缩，Pc）
1 -1.75 1981 177 2 -1.5 1000 82.8 3 -1.25 666 50.7 4 -1.0 498 34.5 5 -0.5 328 18.2 6 0 243 10 7 0.1 10 10 8 10 10 10
请注意在排气口打开时压力的逐渐变化 (0<X0<0.1)。此外，活塞理论上决不会移动到位置 -1.5<X0，但必需使用某些引导方式才能使系统完美和变形。因此，为 -1.75 的冲程计算载荷曲线。