可使用馬克士威方程式以數學形式說明感應加熱的電磁現象。
不同的形式的馬克士威方程式可以寫為:
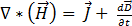 (根據安培定律) [1]
(根據安培定律) [1]
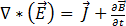 (根據法拉第定律) [2]
(根據法拉第定律) [2]
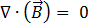 (根據高斯定律) [3]
(根據高斯定律) [3]
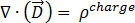 (根據高斯定律) [4]
(根據高斯定律) [4]
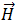 為磁場強度,
為磁場強度, 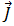 為傳導電流密度,
為傳導電流密度, 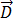 為電通密度,
為電通密度, 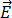 為電場,
為電場, 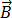 為磁通密度,
為磁通密度, 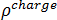 為電荷密度,
為電荷密度, 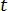 為時間。
為時間。
根據以下方程式,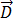 和
和 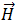 可以透過電磁材料的電容率性質
可以透過電磁材料的電容率性質  及導磁率
及導磁率 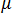 ,與
,與 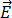 和
和 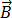 相關聯:
相關聯:
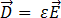 [5]
[5]
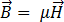 [6]
[6]
可以使用歐姆定律,將馬克士威方程式進一步簡化:
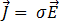 [7]
[7]
將方程式 [5] 和 [7] 代換到方程式 [1] 中,同時留意當電流頻率低於 10 mHz 時,感應電流 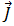 會大於所取代的電流密度
會大於所取代的電流密度 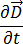 ,因此可以忽略此項,而方程式 [1] 可以寫成:
,因此可以忽略此項,而方程式 [1] 可以寫成:
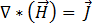 [8]
[8]
由於磁通密度 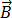 符合方程式 [3] 的零散度,因此可表示為向量磁位
符合方程式 [3] 的零散度,因此可表示為向量磁位 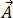 ,使得:
,使得:
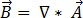 [9]
[9]
將方程式 [9] 代換到方程式 [2] 中,得出:
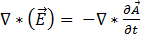 [10]
[10]
因此,
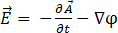 [11]
[11]
其中 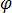 為標量電位。方程式 [7] 現在變為:
為標量電位。方程式 [7] 現在變為:
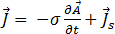 [12]
[12]
其中 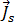 為線圈中來源電流密度的振幅,且是來自:
為線圈中來源電流密度的振幅,且是來自:
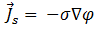 [13]
[13]
將方程式 [6]、[9] 和 [12] 代換到方程式 [8] 中,得出:
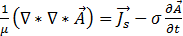 [14]
[14]
現在,將三重積向量恆等式 [15]
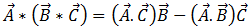 [15]
[15]
用於方程式 [14],得出:
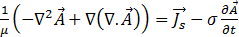 [16]
[16]
現在,留意單元件向量位場
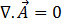 [17]
[17]
接著方程式 [16] 會簡化為
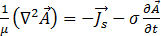 [18]
[18]
對於角頻率 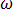 = 2
= 2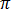 f 和以 rad/s 為單位的正弦穩定狀態,方程式 [18] 將變成:
f 和以 rad/s 為單位的正弦穩定狀態,方程式 [18] 將變成:
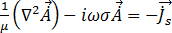 [19]
[19]
當解析時間諧波磁場向量位 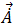 後,可從方程式 [9] 得出磁通密度。導體中的時間諧波感應渦電流
後,可從方程式 [9] 得出磁通密度。導體中的時間諧波感應渦電流 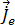 可從方程式 [20] 得出:
可從方程式 [20] 得出:
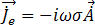 [20]
[20]
而導體中的焦耳熱 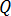 可從下列方程式得出:
可從下列方程式得出:
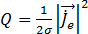 [21]
[21]
焦耳熱為導體中的渦電流所引起的體積熱源,單位為 (W/m3)。
感應加熱中發生的熱傳導現象,是導體內部的熱傳導,可透過所有模擬中使用的暫態熱傳導方程式加以說明。
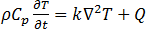 [22]
[22]
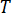 為溫度,
為溫度, 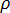 為密度,
為密度, 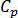 為比熱容量,
為比熱容量, 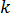 為材料的熱傳導係數,
為材料的熱傳導係數, 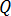 為方程式 [21] 中得出的焦耳熱。
為方程式 [21] 中得出的焦耳熱。