冷卻是純 3D 模具冷卻分析的結果。它使用從 BEM (邊界元素法) 發展而來的數值法。從物理角度來看,BEM 會在求解過程中,將所有邊界視為熱源 (獲得/流失熱)。
模具中的溫度由所有來源的綜合影響決定。
3D 模具的平衡溫度場可由 Laplace 的方程式表示: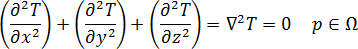
其中: 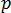 ,且已將邊界條件統一為:
,且已將邊界條件統一為:
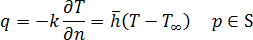
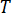 為溫度
為溫度 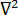 為 Laplace 運算子
為 Laplace 運算子 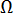 代表模具的表面面積和內部面積
代表模具的表面面積和內部面積
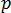 ,且已將邊界條件統一為:
,且已將邊界條件統一為: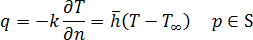
其中:
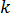 為模具材料的熱傳導係數,
為模具材料的熱傳導係數, 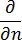 為模具邊界的外向法向導數,
為模具邊界的外向法向導數, 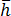 為模具邊界的相等熱傳導係數,
為模具邊界的相等熱傳導係數, 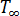 為周圍環境的相等溫度,
為周圍環境的相等溫度, 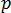 表示特定點,
表示特定點, 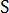 為模具表面 (邊界)
為模具表面 (邊界)
為了瞭解 BEM 如何將所有邊界條件套用至模具溫度場求解,讓我們從加權餘數運算式開始: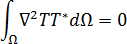
其中,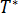 為加權函數。
為加權函數。
您可以使用格林第二恆等式,來將方程式 3 轉換為以下形式: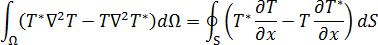
選擇 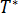 做為方程式 1 的基本解,其定義方式如下:
做為方程式 1 的基本解,其定義方式如下: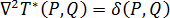
其中,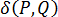 為 Dirac delta 函數。針對 3D 模具,可以將其描述為:
為 Dirac delta 函數。針對 3D 模具,可以將其描述為: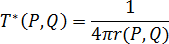
其中:
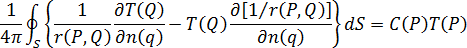
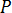 與
與 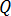 是空間中的兩點,
是空間中的兩點, 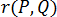 表示這兩點之間的距離,
表示這兩點之間的距離,
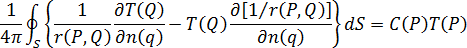
其中:
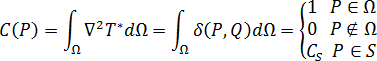 ,
, 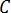 為與內部立體角成比例的常數。
為與內部立體角成比例的常數。
現在,方程式 7 只有邊界積分。因此,如果我們將所有模具表面 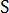 分割成
分割成 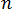 個元素,並假定每個邊界元素上的溫度與溫度梯度恆定,則可以將方程式 7 離散為以下形式:
個元素,並假定每個邊界元素上的溫度與溫度梯度恆定,則可以將方程式 7 離散為以下形式:
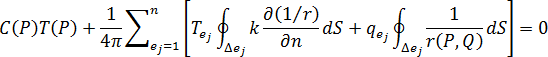
,其中
 分割成
分割成 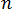 個元素,並假定每個邊界元素上的溫度與溫度梯度恆定,則可以將方程式 7 離散為以下形式:
個元素,並假定每個邊界元素上的溫度與溫度梯度恆定,則可以將方程式 7 離散為以下形式: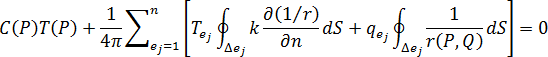
,其中
 為特定元素
為特定元素 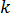 為模具材料的熱傳導係數
為模具材料的熱傳導係數 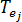 為元素
為元素  的溫度
的溫度
溫度影響項 (或稱為 H 項) (表示溫度對元素  [針對點
[針對點 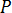 ] 的影響強度),由以下表示式計算得出:
] 的影響強度),由以下表示式計算得出: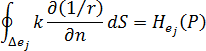
熱通量影響項 (或稱為 G 項) (表示熱通量輸入對元素  [針對點
[針對點 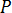 ] 的影響強度),由以下表示式計算得出:
] 的影響強度),由以下表示式計算得出: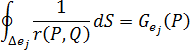
假設 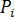 為元素
為元素 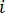 的形心。如果我們用
的形心。如果我們用 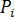 取代方程式 9 中的
取代方程式 9 中的 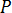 ,那麼我們可以獲得
,那麼我們可以獲得 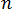 個線性方程式,如:
個線性方程式,如: