Wenn Sie ein Multiscale-Materialmodell für mit kurzen Fasern gefüllten Materialien, wie auf den vorherigen Seiten beschrieben, verwenden möchten, müssen Sie zunächst den Wert des Modellkoeffizienten festlegen. Dies tun Sie, indem Sie das Modell in eine experimentelle Datensammlung für das entsprechende Material einfügen. Um die Modellkoeffizienten definitiv einzufügen, muss die experimentelle Datensammlung im Idealfall die gesamte Bandbreite des Materialverhaltens abdecken. Aus praktischer Sicht ist es jedoch besser, die Anzahl und Komplexität der Test, die ausgeführt werden müssen, zu begrenzen.
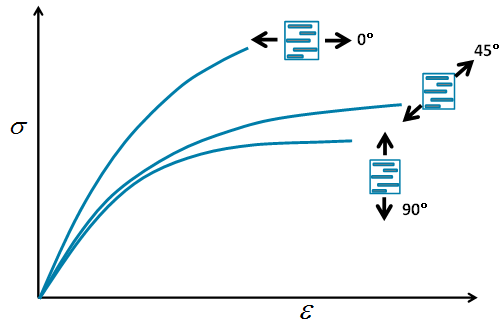
Mit dem aktuellen Modell erzielen Sie mit drei Zugtests bis zum Ausfall gute Anpassungsergebnisse. Das folgende Bild zeigt so eine Sammlung von Zugtests. Es enthält Zuglastdaten in drei verschiedene Richtungen, die relativ zur durchschnittlichen Faserrichtung eines fast vollkommen ausgerichteten Materials verlaufen. In den Zugtests sind 0°-, 45°- und 90°-Zugproben enthalten. Alle Zugproben werden so lange belastet, bis sie schlussendlich brechen.
In den Modellkoeffizienten, die festgelegt werden müssen, sind vier Elastizitäts- und vier Plastizitätskoeffizienten enthalten. In den Elastizitätskoeffizienten sind die Modul- und Poisson-Zahl der Matrixkonstituenten und die Modul- und Poisson-Zahl der Faserkonstituenten enthalten. Die vier Plastizitätskoeffizienten enthalten σ0, n, α und β.
- Sie müssen die vier Elastizitätskoeffizienten bestimmen, indem Sie das Modell anweisen, die ursprünglichen elastischen Reaktionen der 0°-, 90°- und 45°-Zugtest-Zugproben (die Sie von den ersten Datenpunkten der drei Zugtests abrufen können) exakt darzustellen.
- Die vier Plastizitätskoeffizienten werden angepasst, sodass der vollständige Reaktionsverlauf der drei Zugtests vom Modell exakt dargestellt werden kann.