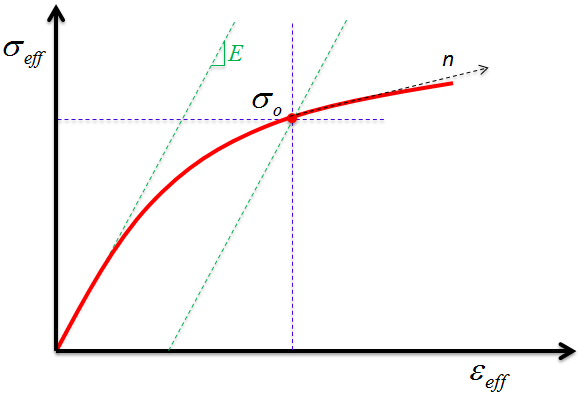
Die Reaktion der Matrixkonstituenten wird mit einem Ramberg-Osgood-Plastizitätsmodell [13] wiedergegeben. Das Modell wurde verbessert und nun kann mit der prognostizierten Plastizitätsreaktion die Empfindlichkeit in Richtung der Last, die relativ zur Faserrichtung verläuft, dargestellt werden. Die effektive gehärtet Fließfestigkeit der Matrixkonstituentenmaterialien kann wie folgt dargestellt werden werden:

wobei σ0 und n die typischen vom (isotropen) Standard-Ramberg-Osgood-Plastizitätsmodell verwendeten Materialparameter darstellen. εp,eff geben die effektive plastische Dehnung der Matrixkonstituentenmaterialien an. Die Fließfunktion ist dann erfüllt, wenn die effektive Spannung der Matrixkonstituenten der gehärteten Fließfestigkeit entspricht.

Bei isotropen Materialien wird die effektive Spannung (Skalar) oft durch die Mises-Spannung wiedergegeben.
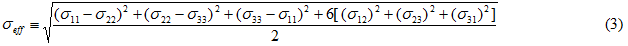
wo zu erkennen ist, dass die Spannungskomponenten die durchschnittliche Spannung im Matrixmaterial darstellen. Ähnlich wie die effektive gehärtete Fließfestigkeit ist auch die effektive Spannung eine Funktion der effektiven plastischen Dehnung εp,eff. Das unmittelbare tangentiale Modul Etan der Matrixkonstituentenmaterialien wird zur Berechnung der Spannungskomponenten benötigt. Etan hängt von der effektiven plastischen Dehnung εp,eff, wie in der untenstehenden Gleichung abgebildet, ab.

In Gleichung 4, H ist das Plastizitätsmodul der Matrixkonstituentenmaterialien und wird wie folgt mit εp,eff dargestellt.

Die Bestimmung der Plastizitätsentwicklung in einem festgelegten Dehnungsinkrement wird soweit reduziert, dass es den Wert εp,eff erreicht. Somit verbleib der Materialzustand auf der erweiterten Fließfläche, z. B. durch das iterative Lösen von Eq. 2 für εp,eff.
Das Ramberg-Osgood-Modell (Eqs. 1-5) prognostiziert eine isotrope Plastizitätsreaktion. Bei kurzen fasergefüllten Kunststoffen, die einen hohen Faserausrichtungsgrad aufweisen, hängt der Plastizitätsgrad vor dem endgültigen Bruch in hohem Maße von der relativ zur Durchschnittsrichtung der Verstärkungsfasern verlaufenden Lastrichtung ab. Das Ramberg-Osgood-Modell kann problemlos so erweitert werden, dass auch Richtungsabhängigkeiten dargestellt werden können. Hierzu ändern Sie einfach das Format der effektiven Spannung (Eq. 3). Im gegenwärtigen Modell wird die modifizierte effektive Spannung wie folgt angegeben:
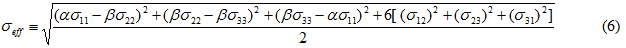
wobei α und β Gewichtungskoeffizienten sind, die verwendet werden, um die Auswirkungen der Spannungskomponenten, die in Richtung der durchschnittlichen Faserrichtung verlaufen, von den Spannungskomponenten, die senkrecht zur durchschnittlichen Faserrichtung verlaufen, abzugrenzen. In dieser richtungsabhängigen Formulierung lauten die Plastizitätsparameter, die die Materialreaktion definieren, wie folgt: σ0, n, α und β.
Wir möchten darauf hinweisen, das das Material nur dann eine starke Richtungsabhängigkeit aufweist, wenn der Grad der Faserausrichtung relativ hoch ist. Sind die Fasern zufällig ausgerichtet, muss die Plastizitätsreaktion zu einer isotropen Reaktion zurück geändert werden. Um diese verhaltensbezogenen Merkmale miteinzuschließen, dürfen die richtungsabhängigen Gewichtungskoeffizienten (α, β) nicht konstant sein. Stattdessen müssen sie Funktionen des Faserausrichtungsgrads sein. In gegenwärtigen Modell wird angenommen, dass α und β lineare Funktionen des Faserausrichtungsgrads, gemessen am höchsten Eigenwert λI des Faserausrichtungstensors, sind.

In den Gleichungen 7 und 8, αm und βm stellen Werte von α und β dar. Sie wurden so optimiert, dass sie sich an die Reaktionscharakteristiken eines stark ausgerichteten Materials mit dem höchsten Faserausrichtungseigenwert λm, I anpassen. θ ist der Wert, den sowohl α als auch β erreichen sollten, wenn eine zufällige Faserausrichtung auftritt. Beachten Sie, dass der Wert λI von 1.0 für ein exakt ausgerichtetes Materials bis zu 1/3 für ein Material mit einer völlig zufälligen Faserorientierung in alle drei Richtungen (vollständig isotrop) reicht.
Es ist jedoch unwahrscheinlich, dass dünne Spritzgussteile eine echte zufällige 3D-Faserverteilung aufweisen. Wahrscheinlicher ist, dass dünne Spritzgussteile einige Positionen enthalten, die eine zufällige Faserorientierung in der Ebene des Spritzgussteils, jedoch nicht in Richtung der Formteildicke, aufweisen (d. h. λI = 1/2). Um diese häufiger auftretende Form der Isotropie zu berücksichtigen, enthalten Eqs. 7 und 8 den Koeffizient (λI - 1/2), wodurch sichergestellt wird, dass wenn λI = 1/2, α und β den selben Wert für θ erreichen und das Material somit isotrop wird.