Bei der Punktspannungsmethode zur Bestimmung der Schraubenfestigkeit (wie im nächsten Abschnitt beschrieben) wird davon ausgegangen, dass der Laminat-Ausfall bei Spannung und Komprimierung auftritt, wenn die normale Spannung im Laminat die letztendliche Stärke in einem definierten Abstand von der Kante der Bohrung erreicht [43]. Diese Abstände werden als charakteristische Längen Rt und Rc bezeichnet. Diese charakteristischen Längen hängen von den Materialeigenschaften des Laminats und dem Verhältnis zwischen Laminat-Breite und Durchmesser der Bohrung ab [44].
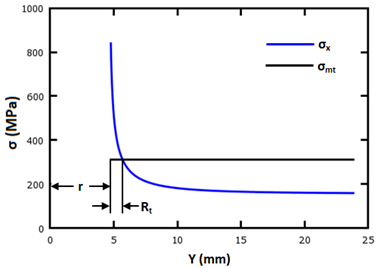
Die charakteristische Länge bei Spannung (Rt) wird mit der Methode von Aluko berechnet [44]. Zunächst betrachten wir ein Prüfstück mit offener Bohrung analog zur Schraubverbindung, die einer Kantenbelastung ausgesetzt wird. Die Zugspannungsverteilung σx wird entlang der Ebene (0,y) wie unten gezeigt berechnet.
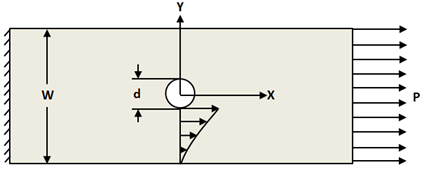
Die Berechnung der Zugspannungsverteilung basiert auf den komplexen Spannungsfunktionen von Lekhnitskii, die später von Aluko für ein orthotropes Laminat mit kreisförmiger Öffnung umgesetzt wurden [45,44]. Die komplexen Spannungsfunktionen φ1 und φ2 werden in den Gleichungen 10 und 11 beschrieben. Die normale Spannung σX ist in Gleichung 12 definiert [44,45].
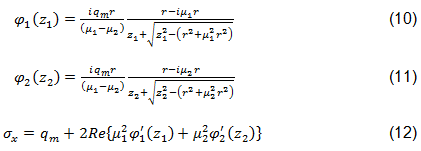
In den Gleichungen 10-12 ist r der Radius der kreisförmigen Öffnung. µ1 und µ2 sind die komplex konjugierten Wurzeln der charakteristischen Gleichung, mit der die orthotropen Eigenschaften des Laminats definiert werden, siehe Gleichung 13 [44]. Die komplexen Variablen z1 und z2 werden nach Aluko definiert, wie in den Gleichungen 14 und 15 gezeigt. qm ist die angewendete Spannung bei unendlich, wie festgelegt durch Gleichung 16 [44].
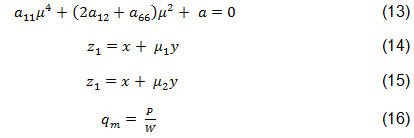
Die Position des Schnittpunkts zwischen der mittleren Zugspannung σmt, wie in Gleichung 17 gezeigt, und die Zugspannungsverteilung σx definieren die Position von Rt wie unten gezeigt [44].
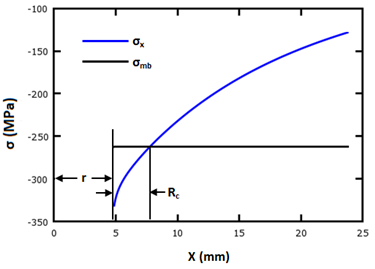
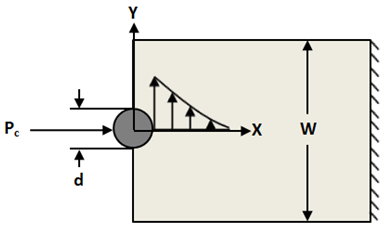
Die charakteristische Länge unter Druck Rc wird nach Aluko berechnet [44]. Bei dieser Methode wird ein Auflager-Testprüfstück auf ähnliche Weise analysiert wie im Fall der Zugspannung. Die Auflager-Spannungsverteilung σx wird entlang der Ebene (x,0) berechnet wie unten gezeigt.
Dies erfolgt mithilfe der komplexen Spannungsfunktionen von Lekhnitskii und Aluko für eine orthotrope Platte mit kreisförmiger Einwirkung [45,44]. Diese Ausdrücke sind in den Gleichungen 18-20 beschrieben [44].
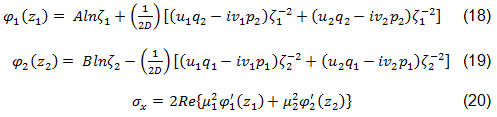
Die Mengen u1, u2, v1, v2, q1, q2, p1, p2 und D sind Konstanten, die von den Materialeigenschaften und den Randbedingungen an der Schnittstelle zwischen Schraube und Platte abhängen [44,46]. Die Mengen A und B hängen von der Belastung, der Verbindungsgeometrie und den Wurzeln der charakteristischen Gleichung µ1 und µ2 ab [44,45]. Das Übertragen des Spannungsfelds aus der komplexen Ebene in das kartesische Koordinatensystem erfolgt mit den komplexen Funktionen ζ1 und ζ2. Diese Funktionen sind in den Gleichungen 20, 21 beschrieben, wobei das Zeichen so gewählt wird, dass beide Größen ζ1 und ζ2 größer oder gleich eins sind [44].
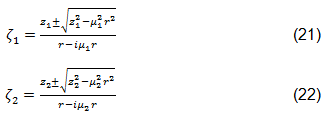
Die Position von Rc wird am Schnittpunkt zwischen Auflager-Spannungsverteilung σx und der mittleren Auflager-Spannung σmb berechnet (definiert in Gleichung 23), die durch die Integration unter dem Einfluss der beliebigen Punktlast Pc auf das Prüfstück ausgeübt wird.

Die folgende Abbildung zeigt die Anwendung dieser Methode.