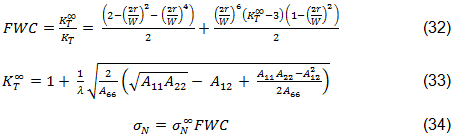Nachdem Sie die charakteristischen Längen ermittelt haben, wird die Kennlinie unter Verwendung der Gleichung 24 erstellt. Diese Kennlinie nach Chang ist unten abgebildet [46]. Wie in der Abbildung gezeigt, ist d der Durchmesser der Bohrung, θ reicht von 0 bis π und rc(θ) definiert die Kennlinie. Diese Linie definiert die Position in der Platte, an der die Festigkeiten in der Ebene geprüft werden und das Ausfallkriterium angewendet wird [44].
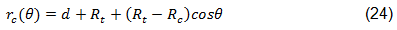
Durch Überlagerung können Sie das gesamte 2D-Spannungsfeld um die Schraube schätzen, das aufgrund der kombinierten Auswirkungen der konzentrierten Auflagerlast Pc und der verteilten Umgehungslast P, angewendet auf unendlich, entsteht. Die kombinierten Ergebnisse werden entlang der Kennlinie nach Chang ausgewertet [46].
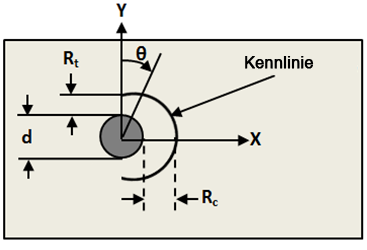
Die komplexen Spannungsfunktionen in dieser Überlagerungsmethode basieren auf den Funktionen nach Lekhnitskii und Aluko, gezeigt in den Gleichungen 25-31 [45,44]. Die tiefgestellten Zeichen b und t bezeichnen die Lösung mit gefüllter Bohrung bzw. die Lösung mit offener Bohrung.
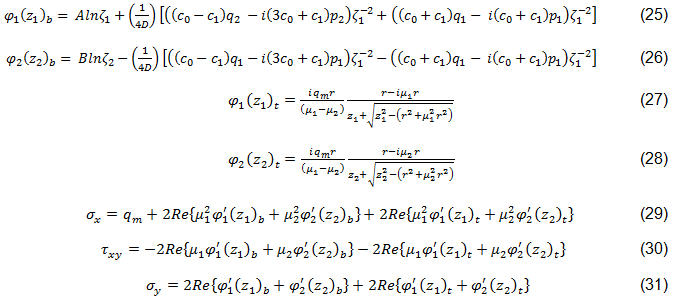
In den Gleichungen 25 und 26 werden c0 und c1 durch Materialkonstanten, Last und Randbedingungen bestimmt [44].
Das Spannungsfeld wird entlang der Kennlinie geschätzt, wobei der finite Breitenkorrekturfaktor (FWC-Faktor) anhand der Gleichungen 32 und 33 berechnet wird [47,44]. KT und KT∞ stellen die Spannungskonzentrationsfaktoren für eine Platte mit finiter bzw. infiniter Breite dar. A11, A12 und A66 sind Komponenten der Laminat-Steifheitsmatrix in der Ebene, r ist der Radius der Bohrung in der Platte und W die Breite der Platte [44,47].
Der FWC-Faktor wird wie in Gleichung 34 gezeigt angewendet, wobei σN und σN∞ die Kerbzähigkeit für eine finite bzw. eine infinite Laminat-Plattenbreite angeben [44].