Das Puck-Kriterium (Ref. 6 und 7) ermittelt das Faserversagen und das Zwischenfaserversagen in unidirektionalen Verbundwerkstoffen. Zudem wird das Zwischenfaserversagen in drei physische Modi und das Faserversagen in zwei physische Modi aufgeteilt. Beim allgemeinen Puck-Kriterium wird der vollständige 3D-Zustand der Spannung und Dehnung verwendet. Die Helius Composite-Implementierung berücksichtigt jedoch nur die mit der klassischen Laminat-Theorie konsistenten Spannungen und Dehnungen in der Ebene.
- Verbundmaterialtyp: Es muss entweder ein kohlefaserverstärktes Polymer (CFP) oder ein glasfaserverstärktes Polymer (GFP) angegeben werden.
- Fasermaterialtyp: Für Lagematerialien, die nicht mit dem Mikromechanik-Modul definiert wurden (Berechnung neuer Lageneigenschaften mit Mikromechanik), müssen Sie das in der Verbundlage verwendende Fasermaterial angeben.
Faserversagen
Das Puck-Kriterium erkennt zwei verschiedene Modi von Faserversagen: Zugversagen und Druckversagen durch Faserknicken. Die Gleichung für das Zugfaserausfallkriterium lautet
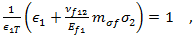
und die Gleichung für das Druckversagen durch Faserknicken lautet
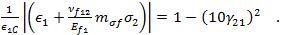
In den obenstehenden Faserausfallkriterien stellen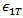 
und 
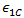die Verbunddehnungen dar, die mit dem Verbundausfall durch Längsdruck und Längsspannung korrespondieren. 
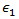stellt hierbei die Uniaxialdehnung im Verbundwerkstoff, 
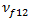die Längs-Poissonzahl der Faser, 
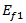das Längszugmodul der Faser, 
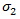die Querspannung des Verbundwerkstoffs und 
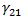die Längs-Scherdehnung im Verbundwerkstoff dar. 
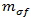dient zur Erfassung der Unterschiede der diagonalen Faser- und Matrixspannungen. Für Kohlefasern 
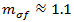und für Glasfasern 
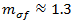. In den oben stehenden Gleichungen wird die Zuggleichung ausgewertet, wenn 
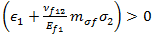, und das Druckkriterium wird ausgewertet, wenn 
.
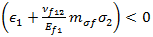Zwischenfaserversagen (Matrixrisse)
Beim Puck-Kriterium umfasst Zwischenfaserversagen alle Arten von Matrixrissen oder Faser-/Matrixablösung. Das Puck-Kriterium erkennt drei verschiedene Zwischenfaserausfallmodi, die sogenannten Modi A, B und C. Diese Zwischenfaserausfallmodi unterscheiden sich durch die Ausrichtung der Bruchebenen zu den Verstärkungsfasern.
- Zwischenfasermodus A
- Modus A entspricht einem Bruchwinkel von 0°. Das Kriterium wird aufgerufen, wenn die Querspannung im Verbundwerkstoff größer als 0 ist (und somit einen Querriss angibt, der lotrecht zur Querlast ist).
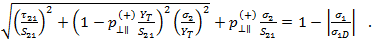
- Zwischenfasermodus B
- Modus B entspricht einer Querdruckspannung (die Rissbildung verhindert) mit einer Längsscherspannung, die unter einer (mit empirischen Konstanten gekoppelten) Bruchfestigkeit liegt.
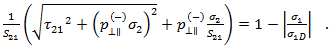
- Das oben genannte Kriterium wird ausgewertet, wenn
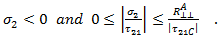
- Zwischenfasermodus C
- Modus C entspricht einer Querdruckspannung (die Rissbildung verhindert) mit einer Längsscherspannung, die groß genug ist, um einen Bruch auf einer geneigten Ebene zur Faserachse zu verursachen. Da der Bruchwinkel im Kontext der klassischen Laminat-Theorie für die Ausfallprognose irrelevant ist, muss er nicht definiert werden, da nur Spannungen und Dehnungen in der Ebene (und keine Reduktion der Materialeigenschaften) enthalten sind. Das Ausfallkriterium für Modus C lautet
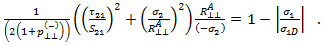
- Das oben genannte Kriterium wird ausgewertet, wenn
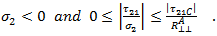
Beschreibung der in den Zwischenfaserausfallkriterien verwendeten Koeffizienten und Terme
Es wird die allgemein akzeptierte Schreibweise verwendet, z. B. ist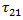 
die Längsschubspannung des Verbundwerksstoffs, 
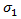die Längsnormalspannung des Verbundwerkstoffs, 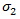die querseitige Normalspannung des Verbundwerkstoffs, 
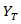Querzugfestigkeit des Verbundwerkstoffs und 
die Querdruckfestigkeit.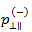 
und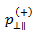 
sind die Neigungen der 
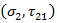-Bruchlinie. Zum Herstellen einer Verbindung zwischen 
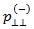und 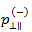, wird von Puck davon ausgegangen, dass die folgende Beziehung gilt:
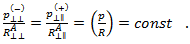
Daher wird 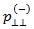folgendermaßen angegeben:
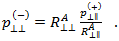
Im Kontext der Spannungen und Belastungen in der Ebene der klassischen Laminat-Theorie kann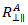 
als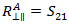 
definiert werden, wodurch Puck 
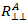wie folgt ausdrücken kann:
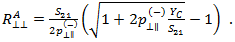
Nun müssen Sie die Werte für 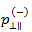und 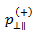festlegen. Puck und Mannigal (2007) empfehlen folgende Werte für 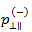und .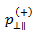
Puck definiert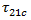 
auch als
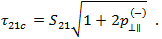
Schließlich muss noch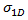 
definiert werden. Hierbei handelt es sich um eine "degradierte" Spannung im Verbundwerkstoff, mit der ein Brechen von einzelnen Fasern vor einem Faserversagen einkalkuliert wird, wodurch lokale Schäden in diesen Bereichen in Form von Mikrorissen und Ablösungen verursacht werden. Um diesen Schwächungseffekt zu berücksichtigen, degradiert Puck die Bruchwiderstände (R) um einen Schwächungsfaktor 
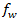. Puck definiert dafür zwei Gleichungen. Die erste gilt für den generalisierten Schwächungsfaktor.
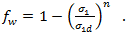
Die Zweite dient dazu, einen anderen Ausdruck des Schwächungsfaktors bereitzustellen, damit die Bruchbedingungen homogen und ersten Grades in Bezug auf die Spannungen bleiben.
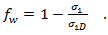
Die beiden sollten für die von Helius Composite berücksichtigten Spannungszustände in der Ebene gleich sein, da keine iterativen Berechnungen der Bruchebenen durchgeführt wird. Aus diesem Grund
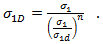
Basierend auf den Empfehlungen von Puck verwendet Helius Composite n=6 für den Exponenten und berechnet empirisch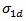 
als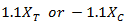 
, je nachdem, welches Vorzeichen 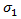hat.