Entnehmen Sie grundlegende Gleichungen für geschlossene lineare Maßketten dem folgenden Bild.
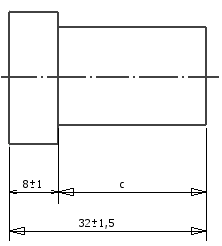
a = 32 ± 1.5 mm, b = 8 ± 1 mm
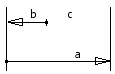
Steigende/fallende Elemente
Wenn das steigende Element ansteigt, steigt das Schlusselement ebenfalls an. Wenn das fallende Element ansteigt, fällt das Schlusselement, sofern andere Elemente der Kette konstant bleiben.
|
Schlusselement: |
1.c = a - b |
|
Abmessung der oberen Grenze des Schlusselements: |
2. c max = a max - b min |
|
Abmessung der unteren Grenze des Schlusselements: |
3. c min = a min - b max |
|
Toleranz des Schlusselements (Gleichung 2 minus Gleichung 3): |
4. c max - c min = a max - a min - (b min - b max |
|
Beispiel |
5. T c = T a + T b |
Im Allgemeinen erfüllen lineare Kettentoleranzen die folgende Gleichung:
![]()
Entsprechend können die Gleichungen 2 und 3 in eine allgemeine Form gebracht werden.
![]()
![]()
Die obere Grenzabmessung des Schlusselements entspricht einer Differenz zwischen der Summe der oberen Grenzabmessung der steigenden Elementen und der Summe der unteren Grenzabmessung der fallenden Elemente.
Die untere Grenzabmessung des Schlusselements entspricht einer Differenz zwischen der Summe der unteren Grenzabmessung der steigenden Elemente und der Summe der oberen Grenzabmessung der fallenden Elemente.
Die Nennabmessung des Schlusselements kann durch Gleichung 1 ausgedrückt werden, z. B. in der folgenden Gleichung:
![]()
Obere Grenzabweichung des Schlusselements:
![]()
Untere Grenzabweichung des Schlusselements:
![]()