Die elektromagnetischen Phänomene der Induktionsheizung werden mathematisch durch Maxwell-Gleichungen beschrieben.
Maxwell-Gleichungen, in Differentialform, können wie folgt geschrieben werden:
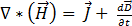(nach Ampere-Gesetz) [1]
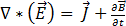(nach Faraday-Gesetz) [2]
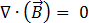(nach Gaußschem Gesetz) [3]
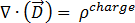(nach Gaußschem Gesetz) [4]
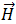ist die Intensität des magnetischen Feldes, 
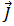ist die Leitungsstromdichte, 
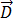ist die Wärmestromdichte, 
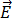ist das elektrische Feld, 
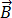ist die Magnetstromdichte, 
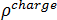ist die Dichte der elektrischen Ladung und 
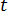ist die Zeit.
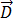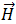und können mit 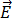und 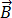durch die Permittivität der elektromagnetischen Materialeigenschaften, 
, und der magnetischen Durchlässigkeit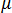 
, entsprechend der folgenden Gleichungen in Bezug gesetzt werden:
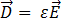[5]
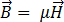[6]
Die Maxwell-Gleichungen können mithilfe des Ohmschen Gesetzes weiter reduziert werden:
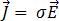[7]
Durch Ersetzen der Gleichungen [5] und [7] in Gleichung [1] und der Beachtung, dass die aktuellen Frequenzen kleiner als 10 MHz sind, ist der Induktionsstrom, 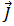, größer als die verschobene Stromdichte, 
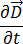, so dass dieser Term ignoriert werden und dann Gleichung [1] geschrieben werden kann:
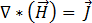[8]
Da die magnetische Flussdichte, 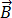, Null-Abweichung von Gleichung [3] erfüllt, kann sie wie folgt als magnetisches Vektorpotenzial, 
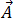, ausgedrückt werden:
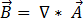[9]
Das Ersetzen von Gleichung [9] in Gleichung [2] ergibt:
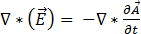[10]
Deshalb
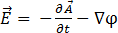[11]
dabei ist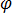 
das elektrische Skalarpotenzial. Gleichung [7] lautet nun:
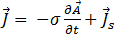[12]
Dabei ist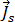 
die Amplitude der aktuellen Dichte in der Spule und wird gegeben durch:
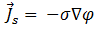[13]
Ersetzen der Gleichungen [6], [9] und [12] in Gleichung [8] ergibt:
[14]
Jetzt, durch Verwendung der dreifachen Produktvektor-Identitätsgleichung 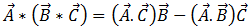[15]
[15]
in Gleichung [4] ergibt sich:
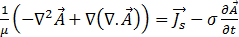[16]
Unter Berücksichtigung, dass jetzt für einen Komponentenvektor mögliche Felder
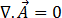[17]
sind, reduziert sich Gleichung [16] auf
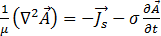[18]
Für den sinusoidalen Bereitschaftszustand mit Winkelfrequenz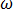 
= 2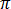
f und Einheiten (rad/s) wird Gleichung [18] zu:
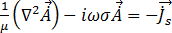[19]
Sobald das zeitharmonische magnetische Vektorpotenzial,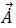 
, aufgelöst ist, ergibt sich die magnetische Feldstromdichte aus Gleichung [9]. Die zeitharmonischen induzierten Wirbelströme, 
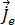, in den Leitern ergeben sich aus Gleichung 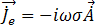[20]:
[20]
, woraus sich die Joulesche Wärme,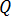 
, in den Leitern ergibt:
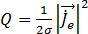[21]
Die Joulesche Wärme ist die volumetrische Wärmequelle mit Einheiten (W/m3), bedingt durch die Wirbelströme im Leiter.
Das Wärmeübertragungsphänomen, das in der Induktionsheizung erfolgt, ist die Wärmeableitung innerhalb des Leiters, und sie wird durch die transiente Wärmeableitungsgleichung beschrieben, die in allen Simulationen verwendet wird.
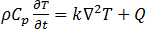[22]
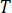ist die Temperatur, 
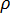ist die Dichte, 
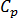ist die spezifische Wärmekapazität, 
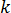ist die Wärmeleitfähigkeit des Materials und 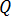- ist die Joulesche Wärmegleichung [21].