Integrationsmethoden

Aktivieren Sie den Befehl: Registerkarte Setup Modell einrichten Parameter Fortgeschritten Integration

Die Informationen auf dieser Seite gelten für die folgenden Analysearten, sofern nicht anders angegeben:

• Mechanische Ereignissimulation (MES)
• Statische Spannung mit nichtlinearen Materialmodellen
• MES Riks Analyse

Drei mögliche Integrationsmethoden sind für eine nichtlineare Spannungsanalyse verfügbar. Sie können über das Dropdown-Feld Für Analysetyp vorgeschlagene Zeitintegrationsmethode auf der Registerkarte Integration ausgewählt werden. (Anmerkungen: MES steht für Mechanischer Ereignissimulator, NLS für nichtlinear statisch und LS für linear statisch).

• Über Allgemein: MES, NLS können hohe Frequenzen ohne Verlust der zeitlichen Integrationsgenauigkeit gedämpft werden. Diese Option eignet sich auch für viele nichtlineare statische Probleme bei Ausführung mit MES. (Die Option Allgemein ist für Analysearten für statische Spannung mit nichtlinearen Materialien oder MES-Riks nicht verfügbar.)
• Die Option Statisch: NLS, LS ist die klassische Newmark-Methode. Sie lässt Hochfrequenzdämpfung zu, wobei jedoch zum Teil die zeitliche Integrationsgenauigkeit verloren geht. Der Verlust der Genauigkeit ist bei statischen Problemen in der Regel nicht wichtig, da die Ergebnisse sich auf den Endzustand beziehen, nicht auf den zeitlichen Verlauf. Beachten Sie, dass eine Zeitintegrationsmethode für statische Probleme benötigt wird, da zur Lösung derartiger Probleme Pseudozeit verwendet wird.
• Bei der Option Statisch II: NLS wird die Wilson-Theta-Methode verwendet. Sie wird für nichtlineare statische Analysen verwendet. Die Option wird auf die Option Statisch: NLS, LS zurückgesetzt, falls nicht Quaderelemente im Modell die Komptabilität erzwingen.

Integrationsmethode Allgemein: MES, NLS

Wenn Sie die Integrationsmethode Allgemein: MES, NLS verwenden, müssen Sie einen Wert im Feld Parameter für (MES-) Integrationsmethode angeben. Gültige Eingabewerte sind 0 und 1, wobei 1 der Vorgabewert ist:

• Mit dem Wert 1 werden hochfrequente Schwingungen und Rauschen herausgefiltert. Es hat sich gezeigt, dass damit stabilere Lösungen erzielt werden (einfachere Konvergenz).
• Mit dem Wert 0 werden mehr hochfrequente Effekte erfasst. Diese Effekte können interessant sein, aber es kann sich auch um äußere hochfrequente Schwingungen (Rauschen) handeln, wodurch die Konvergenz erschwert wird.

Anmerkung: In diesem Zusammenhang sind die Begriffe Hochfrequenz und Niedrigfrequenz in Bezug auf die Abtastrate definiert. Wenn die Abtastrate der Analyse ausreicht, um acht oder mehr Datenpunkte pro Zyklus in der resultierenden Schwingungsfrequenz der Struktur zu erzeugen, hat der Integrationsparameter (0 oder 1) wahrscheinlich kaum Auswirkung auf die Analyseergebnisse. In diesem Fall können die Ergebnisse als Niedrigfrequenzeffekte in Bezug auf die Abtastrate betrachtet werden, und sie werden nicht herausgefiltert. Wenn jedoch der vorgabemäßige Integrationsparameter 1 verwendet wird und wenn die Abtastrate der Analyse fünf oder weniger Datenpunkte pro Schwingungszyklus erzeugt, werden die Verformungs- und Spannungsergebnisse wahrscheinlich stark gedämpft (Überdämpfung). In diesem Fall kann die Schwingungsfrequenz in Bezug auf die Abtastrate als hoch betrachtet werden, und die Hochfrequenzeffekte werden herausgefiltert.

Tipp: Wenn erwartete Hochfrequenzeffekte (die Sie in den Ergebnissen sehen möchten) nicht erfasst werden, empfiehlt es sich, zunächst die Abtastrate zu erhöhen, anstatt den Integrationsparameter von 1 in 0 zu ändern. Die Abtastrate war eindeutig nicht optimal. Für eine akzeptable Genauigkeit müssen etwa zehn oder mehr resultierende Datenpunkte pro Schwingungszyklus der Struktur vorhanden sein.

Tipp: Beim Durchführen von Falltests ergibt der Integrationsparameter 0 im Vergleich zum Integrationsparameter 1 in der Regel genauere Ergebnisse bezüglich der Aufprallzeit und der Aufprallgeschwindigkeit. Andere Analysen mit ähnlichen Freikörperbewegungen (z. B. die Simulation von Projektilbewegungen) weisen wahrscheinlich auch genauere theoretische Zeit- und Geschwindigkeitsergebnisse auf, wenn der Parameter 0 verwendet wird.

Statisch: NLS, LS (klassische Newmark-Integrationsmethode)

Wenn Sie die Integrationsmethode Statisch: NLS, LS verwenden, müssen Sie Werte in den Feldern Erster Parameter für (LS-)Integrationsmethode und Zweiter Parameter für (LS-)Integrationsmethode angeben. Diese Parameter werden wie folgt verwendet:

• Für bedingte Stabilität ist erforderlich: 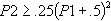, wobei P2 der zweite Parameter und P1 der erste Parameter ist.
• Wenn die Werte P1 = 0.5 und P2 = 0.25 nicht verwendet werden, ist die Genauigkeit der Analyse geringer, aber die Stabilität eines Hochfrequenzereignisses wird erhöht. Wenn z. B ein Objekt auf eine Wand auftrifft und (0.5, 0.25) verwendet wird, dann durchbricht es die Wand nicht, wird aber sehr instabil. Wenn Sie Werte wie (0.7, 0.4) verwenden, tritt geringfügiger Durchbruch auf (Genauigkeitsverlust), aber es kommt zu einem stabilen Rückstoß.
• Die Auswahl der Parameterwerte ist dem Benutzer überlassen. Tests haben gezeigt, dass (0.60,0.31) und (0.7,0.4) häufig wünschenswerte Ergebnisse liefern.
• Anhand der obigen Überlegungen lässt sich erkennen, welche Auswirkung die Erhöhung dieser Parameter hat: je höher sie sind, desto stärker werden hohe Frequenzen gefiltert. Bei einem Problem mit überwiegend hohen Frequenzen ist die Erhöhung der obigen Parameter (0.5, 0.25) nicht geeignet. Die einzige Möglichkeit festzustellen, ob die hohen Frequenzen wichtig sind, besteht im Durchführen des gleichen Problems mit verschiedenen Parameterkombinationen und Prüfen, wie sich die Ergebnisse ändern.

Statisch II: NLS (Wilson-Theta-Integrationsmethode)

Wenn Sie die Integrationsmethode Statisch II: NLS verwenden, wird 1.40 als Wert für Erster Parameter für (LS-)Integrationsmethode verwendet. Die Parameterwerte können nicht benutzerdefiniert sein.

Mit diesem Integrationsschema wird das Gleichgewicht auf einen Zeitpunkt unmittelbar nach dem nächsten Zeitschritt zentriert.

Tipp: Obwohl eine Zeitintegrationsmethode als statisch bezeichnet werden kann, lassen sich die in der Integrationsmethode verwendeten Gleichungen auch auf dynamische Situationen anwenden.