Temperatur eines Tanks

Vorgegeben:

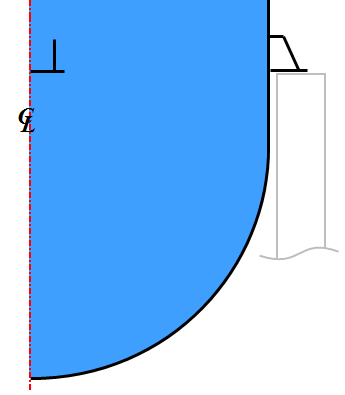
Ein Stahltank mit 0,25 Zoll dicken Wänden ist durch vier Basisplatten abgesichert. Der Tank enthält Wasser bei 150° F und ist teilweise gefüllt. Der Tank befindet sich in einer Umgebung mit einer Temperatur von konstant 70° F.

 

Umgebungsluft 70° F

ho = 1.5E-6 BTU/(s*°F*in2)

 

Heißluft 150° F

hi = 4.7E-7 BTU/(s*°F*in2)

 
   

Erhitztes Wasser 150° F

hi = 1.3E-4 BTU/(s*°F*in2)

Umgebungsluft 70° F

ho = 1.6E-6 BTU/(s*°F*in2)

Suchen: Thermische Spannung und Verschiebung aufgrund der Inhalte.

Für diese spezifische Analyse wird eine zweistufige Analyseprozedur verwendet. Als Erstes wird die Temperaturverteilung des Modells mithilfe einer stationären Wärmeübertragungsanalyse berechnet. Als Nächstes wird die Temperatur in eine Spannungsanalyse importiert, um die thermische Ausdehnung zu berechnen.

In diesem Beispiel geht es um die Durchführung der Analyse, nicht um die Erstellung des Modells. Deshalb wird die Modellgeometrie zur Verfügung gestellt. Das Einrichten des Modells umfasst das Anwenden der Lasten als Konvektion und das Durchführen der Analyse.

  1. Starten Sie Autodesk Simulation.
  2. Öffnen Sie das Tankmodell im Installationsverzeichnis im Modell-Ordner. Wählen Sie Archiv Abrufen, um den Modell-Ordner zu suchen, und wählen Sie tank model.ach.
    1. Aufgrund der Symmetrie wurde ein Viertel des Tanks gezeichnet.
    2. Der Sützpfeiler wurde nicht modelliert. Die Effekte werden berücksichtigt, indem Randbedingungen auf das Modell angewendet werden.
    3. In der Zeichnung des Tanks ist die vertikale Richtung durch +Z dargestellt.
    4. Jeder Teil des Tanks (Tankkörper,Trägerplatte und Stützblech) wird mit einer separaten Teilenummer und unter Verwendung von Plattenelementen gezeichnet. Wenn die Analyse darauf hinweist, dass die Konstruktion über- oder unterdimensioniert ist, kann die Dicke einfach durch Änderung der Plattendicke angepasst werden (in der Elementdefinition).
    5. Die einzelnen Bereiche des Tanks befinden sich auf verschiedenen Flächen, damit die Konvektionslasten in der Wärmeübertragungsanalyse und die Randbedingungen sowie der hydrostatische Druck in der Spannungsanalyse angewendet werden können.
    6. Der Elementtyp, die Elementdefinition und die Materialeigenschaften wurden eingegeben.
    7. Die Einheiten sind auf Pfund, Zoll, Sekunde, ° F und BTU festgelegt.

Die Effekte von Heißwasser (und Luft über dem Wasser) werden in der Analyse simuliert, indem eine Konvektionslast wie folgt angewendet wird:

  1. Verwenden Sie die Flächenauswahloptionen Auswahl Form Punkt oder Rechteck und Auswahl Auswählen Fläche, und klicken Sie an einer Stelle unterhalb des Pegelstandes auf den Tankkörper (Teil 2, Fläche 10).
  2. Klicken Sie mit der rechten Maustaste, und wählen Sie Hinzufügen Konvektion an Fläche.
  3. Geben Sie für den temperaturunabhängigen Konvektionskoeffizienten 1.32E-4BTU/(s*°F*in 2 ) und für die Temperatur 149° F ein.
  4. Klicken Sie auf OK.
  5. Klicken Sie an einer Stelle oberhalb des Pegelstandes auf den Tankkörper (Teil 2, Fläche 8).
  6. Klicken Sie mit der rechten Maustaste, und wählen Sie Hinzufügen Konvektion an Fläche.
  7. Geben Sie für den temperaturunabhängigen Konvektionskoeffizienten 1.97E-6BTU/(s*°F*in 2 ) und für die Temperatur 89° F ein.
  8. Klicken Sie auf OK.

Die Effekte der Umgebungsluft um die Stützbleche werden in der Analyse simuliert, indem eine Konvektionslast angewendet wird:

  1. Klicken Sie auf das Stützblech (Teil 3, Fläche 1).
  2. Klicken Sie mit der rechten Maustaste, und wählen Sie Hinzufügen Konvektion an Fläche.
  3. Geben Sie für den temperaturunabhängigen Konvektionskoeffizienten 1.6E-6BTU/(s*°F*in 2 ) und für die Temperatur 70° F ein.
  4. Aktivieren Sie das Kontrollkästchen Last auf beide Seiten anwenden, da beide Seiten der Platte den gleichen Bedingungen ausgesetzt sind.
  5. Klicken Sie auf OK.

Die Effekte der Wärmeübertragung von der Trägerplatte in die Stützpfeiler und die Konvektion in die Umgebung werden mit einem Wärmestrom für das Modell wie folgt simuliert.

  1. Klicken Sie auf der Trägerplatte an eine beliebige Stelle in der Nähe der Bolzenbohrung (Teil 1, Fläche 7). Beide Platten werden mit der gleichen Bauteil-/Flächennummer gezeichnet, sodass beide ausgewählt werden, wenn sie auf eine Nummer klicken.
  2. Klicken Sie mit der rechten Maustaste, und wählen Sie Hinzufügen Flächenwärmestrom.
  3. Geben Sie für den Betrag -2E-4BTU/(s*in 2 ) ein. Der negative Wert zeigt an, dass Wärme aus dem Modell entfernt wird.
  4. Klicken Sie auf OK.

Verwenden Sie Einrichten Modell einrichten Parameter, um das Dialogfeld Analysenparameter anzuzeigen. Für diese Analyse muss nur der Konvektions-Multiplikator angegeben werden. Dieser Wert steuert die Konvektion und den Wärmestrom. Für die anderen Multiplikatoren ist der Standardwert 1 zulässig, da die Multiplikatoren keine Auswirkungen auf Lasten haben.

Führen Sie die Analyse mit dem Befehl Analyse Analyse Simulation ausführen durch.

Überprüfen Sie die Ergebnisse für die Temperatur, wenn die Analyse abgeschlossen ist: Ergebniskonturen Temperatur Berechnete Temperatur. Der Bereich sollte 92 bis 149° F umfassen, wobei die folgenden Kriterien gelten:

  1. Die Temperatur unterhalb des Wasserpegels ist im Tank sehr gleichmäßig. Der Konvektionskoeffizient des Wassers ist 100 Mal größer als für andere Wärmelasten.
  2. Die obere Bereich des Tanks kühlt sehr schnell ab. Die thermische Spannungsanalyse konnte zwar unter der Annahme durchgeführt werden, dass die Temperatur im gesamten Tank gleichmäßig ist, aber diese Ergebnisse weisen darauf hin, dass diese Annahme möglicherweise nicht richtig ist.
  3. Das Stützblech und die Stützplatten kühlen nur unerheblich ab, obwohl sie sich wie Seitenflossen verhalten.
  4. Die Temperaturergebnisse sind den Temperaturen ähnlich genug, die für die manuellen Berechnungen angenommen werden, sodass eine weitere Wiederholung zu diesem Zeitpunkt nicht gerechtfertigt ist.

Um die Darstellung des Temperaturabfalls im oberen Bereich des Tanks zu verbessern, erstellen Sie einen Pfadplot der Temperatur.

  1. Ändern Sie die Vorderansicht: Ansicht Navigieren Ausrichtung Vorderansicht.
  2. Verwenden Sie ein Rechteck, um die Knoten auf der Kante auszuwählen, die bis in den Bildschirm reichen: Auswahl Form Rechteck, Auswahl Auswählen Knoten, und zeichnen Sie einen engen Rahmen um die Knoten in der linken oberen Ecke.
  3. Klicken Sie mit der rechten Maustaste in den Anzeigebereich, und wählen Sie Pfadplot erstellen. Der Standardplot wird angezeigt, und das Dialogfeld Definition Linienplot ist geöffnet.
  4. Wenn der Temperaturplot nicht richtig aussieht, liegt es wahrscheinlich an der Auflistung der Knoten. Klicken Sie im Dialogfeld Definition Linienplot mit der rechten Maustaste in die Liste Knoten, und wählen Sie Sortieren über Y Koordinate. Wählen Sie im Bereich Anzeigen über die Option Y Abstand. Der Plot sollte glatt sein.

Der nächste Schritt der Analyse ist die Spannungsanalyse. Die Fortsetzung finden Sie auf der Seite Beispiele: Lineare und dynamische Spannung: Thermische Spannung eines Tanks.

Handberechnungen

Ein Nachteil des Plattenelements besteht darin, dass nur eine Konvektionslast pro Fläche angewendet werden kann. Die Konvektion innerhalb des Tanks und die natürliche Konvektion außerhalb des Tanks können nicht einzeln angewendet werden. Diese beiden Effekte müssen kombiniert und auf das Modell als eine Konvektionslast angewendet werden. Die Wärmeübertragung auf der Innen- und Außenseite kann wie folgt beschrieben werden:

Q = hi x A x (150 °F - Tcalc) + ho x A x (70 °F - Tcalc) (1)

Dabei gilt: h ist die Konvektion, A ist die Fläche und Tcalc ist die berechnete Temperatur am Knoten. Im Modell kann die Wärmeübertragung mithilfe eines entsprechenden Konvektionskoeffizienten (he) und einer entsprechenden Konvektionstemperatur (Te) beschrieben werden:

Q = he x A x (Te - Tcalc)

(2)

Wenn diese beiden Gleichungen gleichgesetzt werden, können die Unbekannten he und Te gelöst werden, indem erzwungen wird, dass die berechneten Temperaturen für die übertragene Wärme gleich sind, oder

(hi + ho) x A x Tcalc = he x A x Tcalc (3)

hi x A x 150 °F + ho x A x 70 °F = he x A x Te (4)

Gleichung (3) ergibt die Berechnung des entsprechenden Konvektionskoeffizienten

he = hi + ho (5) 

und die Lösungsgleichung (4) für die entsprechende Umgebungstemperatur sowie die Ersetzungsgleichung (5) ergeben

Te = (150 x hi + 70 x ho) / (hi + ho) (6)

Die in Abbildung 1 dargestellten Konvektionsbedingungen wurden mit dem Rechner für Film-/Konvektionskoeffizienten berechnet, sodass die Gleichungen (5) und (6) die entsprechenden Bedingungen in der Tabelle 1 ergeben, die auf das Modell angewendet werden:

Tabelle 1: Konvektionsberechnungen

Position Innere Konvektion, hi Äußere Konvektion, ho Äquivalente Konvektion, he Äquivalente Umgebungstemperatur, Te
  BTU/(s*°F*in2) BTU/(s*°F*in2) BTU/(s*°F*in2) °F
Unterhalb des Wasserpegels 1.3E-4(Natürliche Konvektion, turbulent, vertikale Platte, 150° F Umgebung, 148° F Wand, Wassereigenschaften bei 149° F) 1.6E-6(Natürliche Konvektion, turbulent, vertikale Platte, 70° F Umgebung, 148° F Wand, Wassereigenschaften bei 109° F) 1.32E-4 149
Luftraum über dem Wasserpegel (oberer Bereich des Tanks) 4.7E-7(Natürliche Konvektion, laminar, horizontale nach unten zeigende Platte, 150° F Umgebung, 105° F kalorische Mitteltemperatur im oberen Bereich, Lufteigenschaften bei 127° F) 1.5E-6(Natürliche Konvektion, turbolent, horizontale nach oben zeigende Platte, 70° F Umgebung, 105° F kalorische Mitteltemperatur im oberen Bereich, Lufteigenschaften bei 88° F) 1.97E-6 89

Die Wärmeleitung von der 4 x 8 Zoll großen Unterlage kann geschätzt werden, indem Gleichungen für eine Seitenflosse verwendet werden. Stellen Sie sich den Tank auf einem Betonpfeiler von 4 x 8 Zoll vor {k = 1.3E-5 BTU/(s*°F*in)}. Das Ende des Pfeilers am Tank wird auf einer hohen Temperatur gehalten, und die Abkühlung am Pfeiler {h = 1.6E-6 BTU/(s*°F*in 2 )} erstellt eine Anordnung, die mit einer Seitenflosse identisch ist. Nehmen Sie für die Annäherungsmethode an, dass der Pfeiler lang genug ist, sodass das Ende am Boden Umgebungstemperatur hat{Tamb = 70° F}. Die Gleichung für den Wärmeverlust einer solchen Seitenflosse lautet

Q = (T-Tamb) [h x Umfang x k x A ]0.5 (7)

Wenn die Unterlage 135° F beträgt, ergibt diese Gleichung

Q = (135-70 °F) [1.6E-6 BTU/(s*°F*in2) x 24 in x 1.3E-5 BTU/(s*°F*in) x 32 in2]0.5 = 8.2E-3 BTU/s

oder pro Fläche: Q = Q = (8.2E-3 BTU/s)/(32 in2) = 2.6E-4 BTU/(s*in2).

Übergeordnetes Thema: Stationäre Wärmeübertragung