Wenn das Kontrollkästchen Steifigkeitsmatrix und Kraftvektor auf der Registerkarte Ausgabe im Dialogfeld Analyseparameter aktiviert ist, werden die Steifigkeits- und Massematrizen in eine Dateiname.mtx-Textdatei ausgegeben. In diesem Dokument wird beschrieben, wie Sie die Steifigkeitsmatrix für Benutzer interpretieren, die sie für andere Zwecke verwenden möchten. Das Dateiformat variiert je nach verwendeten Solver.
Unterraum-Solver
Die erste Zeile der Matrixausgabedatei (siehe Abbildung 1) enthält die folgenden Werte:
1. Die gesamte Steifigkeitsmatrix ist möglicherweise zu groß zum Lösen als großer Zahlenblock. Die Matrix kann möglicherweise in kleinere Blöcke geteilt werden. Die Anzahl der Zeilen der Steifigkeitsmatrix, die in einem Block angezeigt wird, wird durch die Gleichungen pro Block dargestellt.
2. Die Anzahl der Spalten in der Steifigkeitsmatrix wird durch die Bandbreite dargestellt. Jede Zeile der Steifigkeitsmatrix kann in mehrere Zeilen der .mtx-Datei gedruckt werden, mit bis zu fünf (5) Zahlen pro Zeile.
3. Blöcke: ist die Anzahl der Blöcke in der Lösung und die Anzahl der Blöcke, in die die Steifigkeitsmatrix aufgeteilt wird. Für die Modalanalyse beträgt die minimale Anzahl von Blöcken immer zwei (2).
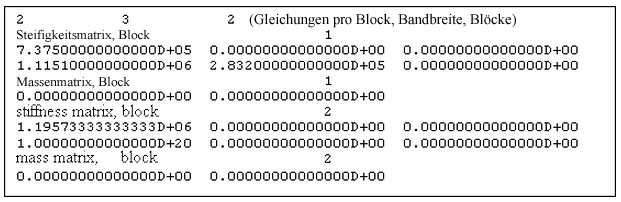
Abbildung 1: Beispielsteifigkeitsmatrix (.mtx)
Um die Einträge in der Steifigkeitsmatrix zu verstehen, sehen Sie sich Abbildung 2 an. Die Steifigkeitsmatrix ist quadratisch und symmetrisch. Die erste Zahl in jeder Zeile der Matrix (wobei Sie beachten müssen, dass für jede Zeile möglicherweise mehrere Ausgabelinien erforderlich sind) liegt der Steifigkeitsausdruck auf der Diagonalen. Die Ausdrücke danach gelten für die obere Hälfte der Steifigkeitsmatrix. Jede Zeile in der Ausgabe enthält jedoch die Bandbreite der Anzahl Ausdrücke. Deshalb wird jeder nachfolgenden Ausgabezeile eine Null (0) hinzugefügt.
Wie korrelieren die Begriffe in der Steifigkeitsmatrix mit dem Modell und den Knoten? Dies ist aus Abbildung 3 ersichtlich. FHG, was für Freiheitsgrad steht, bezieht sich auf einen bestimmten Knoten und eine bestimmte Bewegung: entweder eine Translation oder Drehung. Diese Korrelation kann durch Drucken der Gleichungszahlen mit der Option Global: Ausgabe: Gleichungszahlendaten ermittelt werden. Abbildung 4 zeigt ein Beispiel für einen Ausdruck der Gleichungszahlen, die in der Zusammenfassungsdatei (.ml) dargestellt werden. In einigen Fällen ist es möglicherweise einfacher, die Bandbreitenminimierung (Global: Optionen: Bandbreitenminimierung vermeiden) zu vermeiden.
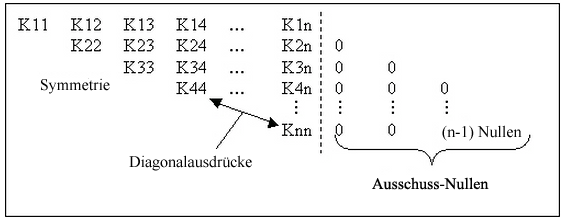
Abbildung 2: Steifigkeitsmatrix
Verschieben Sie alle Werte nach links, und Sie erhalten eine quadratische Matrix von n x n. Dies entspricht der Ausgabe in der .mtx Datei.
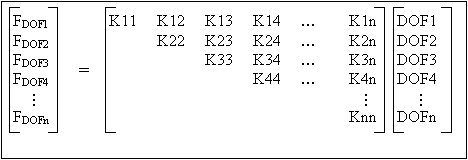
Abbildung 3: System von Gleichungen
DOFi ist eine Richtung (X, Y oder Z) und Komponente (Translation oder Drehung), die aus den Gleichungszahlen ermittelt werden kann.
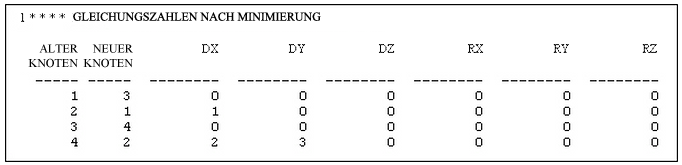
Abbildung 4: Gleichungszahlen aus Zusammenfassungsdatei (.ml)
Solver
Es gibt zwei Abschnitte der vom Solver erstellten Dateiname.mtx-Datei. Der erste Abschnitt enthält die Werte auf der Diagonalen der Matrix für die Steifigkeitsmatrix und die Massenmatrix. Es gibt vier Spalten wie in Abbildung 5 weiter unten dargestellt.
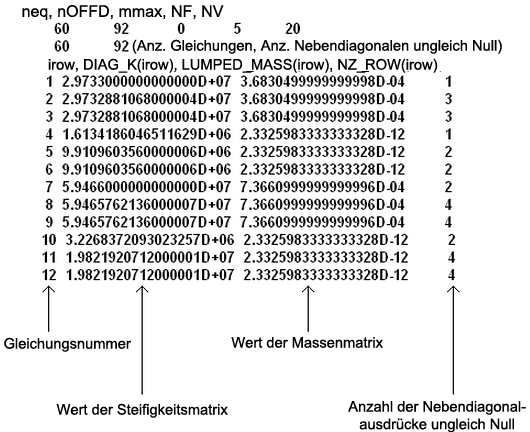
Abbildung 5: Teil des ersten Abschnitts einer .mtx-Datei
Deshalb defineirt der erste Abschnitt die Diagonale der Steifigkeit und Massenmatrizen. Da die Massenmatrix keine Werte ungleich Null entfernt von der Diagonalen aufweist, ist die Massenmatrix vollständig definiert. Der zweite Abschnitt besteht aus drei Spalten, wie in Abbildung 6 dargestellt.

Abbildung 6: Teil des zweiten Abschnitts einer .mtx-Datei
Die ersten und zweiten Abchnitte müssen verwendet werden, um den Rest der Steifigkeitsmatrix zu erstellen. Die vierte Spalte des ersten Abschnitts definiert, wie viele Werte ungleich Null sich in dieser Zeile befinden. Bezugnehmend auf Abbildung 5 enthält die erste Zeile nur 1 nicht-diagonalen Wert ungleich Null und die zweite Zeile drei nicht-diagonale Werte ungleich Null. Daher befindet sich in Abbildung 6 der Wert für Index 1 in der ersten Zeile und die Werte für die Indizes 2, 3 und 4 in der zweiten Zeile. Diese Methode kann erweitert werden, um die Zeile für jeden Ausdruck zu ermitteln. Nur die Ausdrücke ungleich Null werden in der zweiten Spalte angezeigt. Der Wert in der dritten Spalte definiert, in welcher Spalte der Matrix sich der Ausdruck befindet. Bezugnehmend auf Abbildung 6 befindet sich der erste Wert in Spalte 55. Die Werte in der ersten Zeile der Spalten 2-54 betragen deshalb alle 0. Ebenso betragen alle Werte in Zeile 2 in den Spalten 56-60 Null. (Der Wert in Spalte 1 befindet sich auf der Diagonalen und wird daher im ersten Abschnitt definiert). In der zweiten Zeile sind 0-Werte in den Spalten 3-5, 7-55 und 57-59 enthalten. Die Steifigkeitsmatrix ist symmetrisch, daher sind nur die Werte oben rechts von der Diagonalen definiert. Verwenden Sie die Symmetrie zum Definieren der unteren linken Hälfte.