Theoretische Grundlage von Ereignissimulationen

Die Ereignissimulation erfolgt durch Simulieren eines physischen Ereignisses in einem virtuellen Labor. Bei der Durchführung einer Konstruktionsanalyse mithilfe einer Ereignissimulation muss von einem anderen Standpunkt ausgegangen werden als bei der klassischen Spannungsanalyse.

In der Maschinenbau-Ausbildung lernen wir, dass Spannung eine Funktion der Kraft ist, oder σ= f(Kraft). Die Verformung, oder Verschiebung, ist ebenfalls eine Funktion der Kraft, oder d = g(Kraft). Bei der Ereignissimulation wird jedoch davon ausgegangen, dass die Konstruktionskraft unbestimmt ist durch irgendeine Art von Aktion oder Bewegung erzeugt wird. In diesem Szenario sind Kraft und Spannung Funktionen der Verschiebung oder Verformung, d. h. Kraft = f(d) und σ = g(d). Die Verformung oder Verschiebung wird direkt anhand der zugrunde liegenden physikalischen Gleichungen berechnet.

Vergleich zwischen mechanischen Ereignissimulationen und klassischen Verfahren

Die Unterschiede zwischen der klassischen Spannungsanalyse und der Ereignissimulation sollen nun am Beispiel eines einfachen Auslegerbalkens veranschaulicht werden.

Gemäß einem Maschinenbau-Handbuch wird für einen Auslegerbalken, auf den am Ende gegenüber dem befestigten Ende eine Kraft ausgeübt wird, die maximale Spannung (bei A) wie folgt bestimmt:

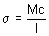
[1]

Dabei ist M das durch die Kraft F (M = Fl) erzeugte Moment, c der Abstand zwischen der neutralen Achse und der Kante des Balkens (c = t/2) und I das Flächenträgheitsmoment (I = wt 3 /12). Dieses Ergebnis wird erzielt, indem die Biegung eines Balkens mit dem hookeschen Gesetz (|F| = k|d|) berücksichtigt wird. Gemäß diesem Gesetz ist die Kraft eine lineare Funktion der Verschiebung. Diese Aussage bildet die Grundlage der klassischen Spannungsanalyse und der modernen Spannungsanalysemethode der finiten Elemente.

Bei der Finite-Element-Analyse wird die Matrixgleichung {F} = [K]{d} für den Verschiebungsvektor {d} anhand des Kraftvektors {F} und der Steifheitsmatrix [K] gelöst. Anschließend werden die Spannungen mithilfe der Gleichung {σ} = E {ε} berechnet, wobei {ε} der Deformationsvektor ist, der einen normierten Verschiebungsvektor darstellt. E ist das Elastizitätsmodul, das der hookeschen Konstante k entspricht.

Dies ist unproblematisch, wenn der Balken stets stationär ist, was die einzige gültige Anwendung von Gleichung [1] ist. In der Maschinenbaupraxis ist der statische Fall nie für die Konstruktion ausschlaggebend. Bei der Konstruktion muss vom Worst-Case-Szenario ausgegangen werden, das in der Regel dann eintritt, wenn der Balken in Bewegung ist und die Kräfte und somit auch die Spannungen größer sind als im statischen Zustand.

An diesem Punkt des Konstruktionsvorgangs wird die Ereignissimulation relevant. Sie können das gesamte Ereignis simulieren, anstatt lediglich eine statische Lösung zu erhalten. Ein nützlicher Nebeneffekt der Ereignissimulation sind die durch die Bewegung erzeugten Kräfte. Gemäß dem zweiten newtonschen Gesetz gilt

F=ma [2]

oder Kraft ist gleich Masse mal Beschleunigung. Die Masse ist eine inhärente Eigenschaft der Materie, und die Beschleunigung ist die Änderung der Geschwindigkeit. Dieses Gesetz quantifiziert die Tatsache, dass die Masse die Eigenschaft der Materie ist, die Bewegungsänderungen einen Widerstand entgegensetzt. Beachten Sie, dass ein Körper mit der Ruhemasse m unter Einfluss der Schwerkraft eine Kraft mg erzeugt, wobei g die Beschleunigung aufgrund der Schwerkraft ist. In den besonderen Fällen einer konstanten Beschleunigung (Schwerkraftfeld in der Nähe der Buchoberfläche) und von Ereignissen von kurzer Dauer (z. B. der Länge Δt) kann die Gleichung [2] wie folgt umformuliert werden:

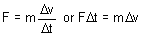
[3]

wobei Δv der Betrag der Geschwindigkeitsänderung während der Zeit Δt ist. Eine Kraft von 1.000.000 lb., die über 0,000001 Sekunden wirkt, erzeugt denselben Impuls (oder dieselbe Änderung der Schwungkraft) wie eine Kraft von 1 lb. über 1 Sekunde.

Bei der Ereignissimulation wird das zweite newtonsche Gesetz wie folgt mit dem hookeschen Gesetz kombiniert:

F = ma = -kd, or

ma + kd = 0  

[4]

Das negative Vorzeichen vor k bedeutet, dass die Kraft in entgegengesetzter Richtung der Verschiebung wirkt. Beachten Sie außerdem, dass die unklare Menge der Kraft ausgelassen werden kann, und dass das Konzept der Zeit durch die Beschleunigung eingeführt wurde. Bei der Simulation realer Probleme müssen auch die Dämpfung oder die Reibung berücksichtigt werden. Solche dissipierenden Kräfte können wie folgt modelliert werden:

F=-cv [5]

wobei v der Geschwindigkeit und c einer Konstante entspricht. Beachten Sie, wie die Dissipation ebenfalls die Bewegung behindert. Durch Kombinieren der Gleichungen [4] und [5] erhalten wir Folgendes:

ma+cv+kd = 0 [6]

oder in Matrix-Form:

[M]{a} + [C]{v}+[K]{d} =0 [7]

Dies ist die grundlegende Gleichung des virtuellen Maschinenbaus. Beachten Sie, wie hiermit die Kombination aus Bewegung, Dämpfung und mechanischer Verformung modelliert wird. Wenn die Spannungen weiterhin von Interesse sind, können Sie diese während der Analyse jederzeit mithilfe der Formel {σ} = E {ε} berechnen, wobei {ε} (der Spannungsvektor) leicht anhand des Verschiebevektors {d} ermittelt werden kann. Der virtuelle Maschinenbau bietet die nötigen Konstruktionsmöglichkeiten für das Worst-Case-Szenario. Selbst bei dem einfachen Beispiel des Auslegerbalkens wäre die Lösung von Gleichung [7] nicht durch eine Handrechnung zu erreichen gewesen. Dank der modernen Computertechnologie wird die Lösung komplexerer Probleme auf die praktische Ebene reduziert.

Zahlenbeispiel

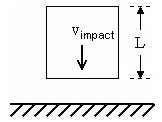
Die Möglichkeiten des virtuellen Maschinenbaus wollen wir nun anhand eines Zahlenbeispiels demonstrieren. Angenommen, ein Würfel mit der Masse m prallt auf eine starre Oberfläche entlang einer Fläche. Uns interessiert die maximale Verformung, die der Würfel erfährt. Zunächst ermitteln wir die maximale Stauchungslänge per Handrechnung. Anschließend lösen wir dasselbe Problem mithilfe des virtuellen Maschinenbaus und vergleichen die Ergebnisse.

Würfel vor dem Kontakt.

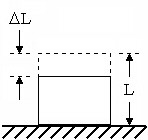
Würfel zum Zeitpunkt der maximalen Verformung.

Gemäß dem zweiten newtonschen Gesetz wird die Aufprallkraft durch Gleichung [1] bestimmt. Unter Beachtung der Prinzipien der klassischen Physik gehen wir davon aus, dass sich die gesamte Masse des Würfels an seinem Schwerpunkt befindet. Zudem sei angenommen, dass die Beschleunigung während des Aufpralls für jede beliebige Position auf dem Würfel konstant ist. Dann nimmt Gleichung [1] folgende Form an:

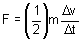
[8]

Dabei entspricht Δv der Geschwindigkeitsänderung an der Oberseite des Würfels während des Aufprallintervalls Δt. Der Faktor 1/2 in Gleichung [8] ist erforderlich, da wir Gleichung [1] am Schwerpunkt anwenden, wobei in der Mitte des Würfels eine halb so große Beschleunigung wie an der Oberseite des Würfels zu erwarten ist. Anders ausgedrückt erwarten wir, dass sich die Oberseite des Würfels nach dem Kontakt doppelt so schnell bewegt wie sein Schwerpunkt. Die Annahme der konstanten Beschleunigung in Verbindung mit der grundlegenden Bewegungslehre ermöglicht uns, einen Ausdruck für den Grad der Verformung des Würfels während des Aufpralls zu ermitteln:

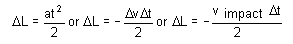
[9]

Dabei entspricht v impact der Geschwindigkeit des Würfels und somit seiner Oberseite in dem Moment, in dem der Kontakt stattfindet. Das negative Vorzeichen in Gleichung [9] ist erforderlich, da Δv negativ ist und wir einen positiven Wert für ΔL suchen. Beachten Sie, dass Δv durch lediglich v impact ersetzt wurde, da sich die Oberseite des Würfels zum Zeitpunkt der stärksten Verformung nicht bewegt.

Gemäß dem hookeschen Gesetz ist die auf den Würfel wirkende Kraft definiert durch

[F=-kDL] [10]

Durch Kombinieren der Gleichungen [8] bis [10] ergibt sich Folgendes:

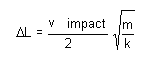
[11]

Indem k durch E (k = EL für einen Würfel der Länge L, der sich entlang einer senkrecht zu einer Fläche verlaufenden Achse verformt) ausgedrückt wird, erhalten wir:

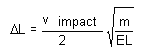
[12]

Mithilfe der Software simulieren wir dasselbe Aufprallproblem. Wir modellieren einen Würfel mit der Länge (L) 1,0 Zoll und der Masse (m) 0,000253 lbm. Er besteht aus einem Material mit einem Elastizitätsmodul E von 107lb/Zoll2. Das simulierte Ereignis entspricht dem Fallenlassen des Würfels aus einer Höhe von 100. Das Ergebnis ist eine Aufprallgeschwindigkeit (vimpact) von 278 Zoll/s unter Einfluss eines Schwerkraftfelds der Stärke 386,4 Zoll/s2. Die Software prognostiziert eine maximale Verformung (ΔL) von 0,000694 Zoll, was sich günstig zum Wert von 0,000699 Zoll verhält, der sich aus Gleichung [6] ergibt.

Dieses Beispiel veranschaulicht, wie schwer es ist, ein einfaches Aufprallproblem zu analysieren, ohne eine digitale Produktentwicklungssoftware zu Hilfe zu nehmen. Stellen Sie sich vor, wie aufwändig, wenn nicht gar unmöglich eine Handrechnung für eine etwas komplexere Geometrie ist. Sie können auf die gewöhnliche klassische Finite-Elemente-Methode (FEM) zurückgreifen. Eine solche Analyse vernachlässigt die (Gesamt-)Bewegung, wäre jedoch unter Umständen ausreichend, wenn die Aufprallkraft bekannt wäre. Die Unzulänglichkeiten treten vor allem deshalb auf, weil bei einer solchen Analyse die Schwingungen unberücksichtigt bleiben, die während des eigentlichen Aufpralls durch Schwankungen in der Kraft freigesetzt werden.

Verfahren zur Schätzung der Kraft

Es gibt drei häufig verwendete Verfahren zur Schätzung von Kraftwerten zur Eingabe in der klassischen FEM: Erfahrung, Starrkörperdynamik-Analyse und physikalische Versuche.

Schlussfolgerungen

Mithilfe der Ereignissimulation kann ein vollständiges physisches Ereignis mit der geringstmöglichen Anzahl von Annahmen modelliert werden. So muss z. B. keine statische Situation angenommen und keine Schätzung der Werte für die aus einer Bewegung resultierenden Kräfte vorgenommen werden. Darüber hinaus hat die Ereignissimulation den nützlichen Nebeneffekt, dass jeder einzelne Schritt des Ereignisses dokumentiert und nicht nur eine Momentaufnahme des Ergebnisses erstellt wird.

Übergeordnetes Thema: MES - Nichtlinear-strukturell