Schädigung - Theoretische Beschreibung

Übersicht:

Das Schädigungsmodell simuliert den Schädigungsbeginn und das fortschreitende Wachstum für elastisch-sprödes, orthotropes Material, z. B. einen Verbundwerkstoff. Das Modell soll in erster Linie der Simulation von faserverstärkten Verbundwerkstoffen dienen. Das Schädigungsmodell beschreibt drei Phasen des Materialverhaltens:

1. das Verhalten des unbeschädigten Materials, das linear-elastisch sein muss
2. der Schädigungsbeginn
3. das fortschreitende Schädigungswachstum

Im Modell ist die Schädigung in Materialien durch die Degradierung der Steifheit gekennzeichnet. Es wird davon ausgegangen, dass die Fasern der Verbundwerkstoffe parallel sind und in der Richtung der Materialachse 1 des Elements verlaufen. Es werden vier verschiedene Ausfallarten berücksichtigt:

• Faserreißen bei Spannung
• Faserbeulen und -knicken bei Komprimierung
• Matrixriss bei Querschubspannung und Scherung
• Matrixbruch bei Querschubkomprimierung und Scherung

Das Materialverhalten wird definiert als σ = C_dε, wobei C_d die elastische Matrix ist, die die Schädigung widerspiegelt und folgendermaßen berechnet wird:

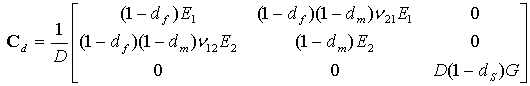
Dabei gilt:

• D=1-(1-d_f)(1-dm)ν₂₁ν₁₂ν
• d_f stellt die Faserschädigung dar.
• d_m stellt die Matrixschädigung dar.
• d_s stellt die Scherschädigung dar.
• E₁ ist das Elastizitätsmodul in der Faserrichtung.
• E₂ ist das Elastizitätsmodul in der Richtung senkrecht zu den Fasern.
• G ist das Schermodul.
• ν₂₁und ν₁₂ sind Poisson-Zahlen.

Schädigungsbeginn

Bei den Kriterien für den Schädigungsbeginn werden vier unterschiedliche Schädigungsmodi berücksichtigt, die sich folgendermaßen darstellen:

Modus I: Faserspannung (> =0)
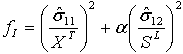
Modus II: Faserkomprimierung (< 0)
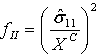
Modus III: Matrixspannung (> =0)
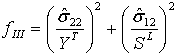
Modus IV: Matrixkomprimierung (< 0)

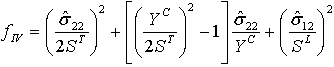
Dabei gilt:

• f_I, f_II, f_III, f_IV sind die Variablen, die mit den Kriterien für den Schädigungsbeginn verbunden sind. Ein Wert von 1.0 oder höher gibt an, dass das Anfangskriterium erreicht wurde.
• X^T stellt die Zugfestigkeit in Längsrichtung dar.
• X^C stellt die Druckfestigkeit in Längsrichtung dar.
• Y^T stellt die Zugfestigkeit in Querrichtung dar.
• Y^C stellt die Druckfestigkeit in Querrichtung dar.
• S^L stellt die Scherfestigkeit in Längsrichtung dar.
• S^T stellt die Scherfestigkeit in Querrichtung dar.
• α stellt den Koeffizienten dar, der bestimmt, inwiefern die Scherspannung zum Kriterium für die Faserfestigkeit beiträgt, und 0<=α <=1 festlegt.

, und sind die Komponenten des effektiven Spannungszugs,, der sich aus =Mσ berechnet. σ ist die Nominalspannung und M ist der Schädigungsoperator, der wie folgt definiert ist:

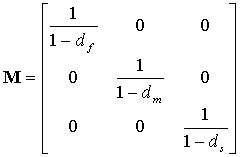
Die internen Schädigungsvariablen d_f, d_m und d_s werden von den Schädigungsvariablen d_ft, d_fc, d_mt und d_mc entsprechend der vier Modi abgeleitet:

d_f = …

• d_ft, wenn 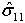>= 0
• d_fc, wenn 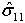< 0

d_m = …

• d_mt, wenn 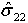>= 0
• d_mc, wenn 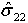< 0

d_s = 1-(1-d_ft)(1-d_fc)(1-d_mt)(1-d_mc)

Die Gleichungen für die Schädigungsvariablen d_ft, d_fc, d_mt, und d_mc sind unten angegeben.

Schädigungsentwicklung:

Basierend auf dem Schädigungsbeginn im vorherigen Abschnitt wird hier die Entwicklung der Schädigungsvariablen für jeden Modus definiert. Um die Netzabhängigkeit bei der Materialerweichung zu verringern, werden Äquivalentspannung und Verschiebung eingeführt.

Äquivalentspannungen und Verschiebungen sind für jeden der vier Schädigungsmodi definiert:

• Faserzugmodus:

  

  

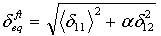
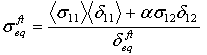
• Faserdruckmodus:

  

  

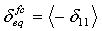
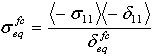
• Matrixzugmodus:

  

  

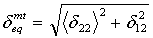
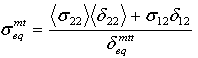
• Matrixdruckmodus:

  

  

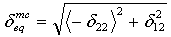
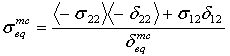
wobei δ_ij = L_cε_ij und L_c, die charakteristische Länge, als Quadratwurzel des Integrationspunktbereichs berechnet wird. Der Operator <x> ist der Macauley-Operator, der als <x> = (x +|x|)/2 definiert ist.

Basierend auf den Äquivalentspannungen und Verschiebungen wird die Schädigungsvariable wie folgt berechnet:

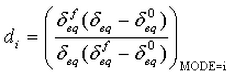
wobei i den vier Modi I bis IV entspricht (oder d_ft, d_fc, d_mt und d_mc). Die Ergebnisse liegen im Bereich von 0 bis 1, wobei 0 angibt, dass keine Schädigung vorliegt und das Element eine volle Last tragen kann, und 1 gibt an, dass eine vollständige Schädigung vorliegt und das Element keine Last in der entsprechenden Richtung tragen kann.

δ⁰_eq und σ⁰_eq sind die äquivalente Anfangsverschiebung und Spannung, bei der das Anfangskriterium erreicht wurde. Sie sind wie folgt definiert:

.

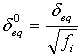
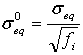δ^f_eq = 2G^c_i/σ⁰_eq ist die äquivalente Verschiebung, bei der das Material in diesem Ausfallmodus vollständig beschädigt ist, wobei G^c_i, die durch den Ausfallmodus i verbrauchte Energie (Spannung oder Komprimierung) die Schädigungsentwicklung bestimmt.

Die maximale Größe des finiten Elements für jedes Schädigungsgesetz ist L_c <= 2 * E_iG^c_i / (X_i)², wobei Eⁱ, G^c_i und Xⁱ jeweils das Elastizitätsmodul, die Bruchenergie und die Bruchfestigkeit darstellen. i entspricht wiederum den vier Schädigungsmodi von I bis IV (oder entsprechende Bezeichnung abhängig von der Variablen).

Stabilisierung bei Schädigung und viskose Regularisierung:

Ein verallgemeinertes Duvaut-Lions-Schema zur viskosen Regularisierung wird eingeführt, um Konvergenzschwierigkeiten durch Materialerweichung und Steifigkeitsdegradation in einer impliziten Analyse zu überwinden. Im Regularisierungsschema wird eine viskose Schädigungsvariable definiert als

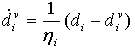
η_i ist der Viskositätskoeffizient, der die Relaxationszeit des viskosen Systems darstellt, und d_i ist die Schädigungsvariable, die im nichtviskosen Modell evaluiert wird, wobei i einen Schädigungsmodus angibt (I bis IV, oder ft, fc, mt und mc entsprechend der Variablen). Die regularisierte Schädigungsvariable wird aktualisiert als:

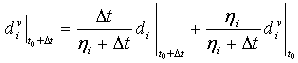
Das beschädigte Verhalten des viskosen Materials wird als σ = C_d(dν)ε angegeben. Ein kleiner Viskositätsparameter verbessert in der Regel die Konvergenzrate des Modells im Erweichungsschema, ohne die Ergebnisse zu beeinflussen.

Weitere Analysen von Interesse sind:

• Ergänzende freie Energiedichte:

  

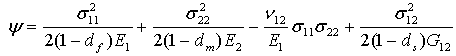
• Schädigungsenergie:

  

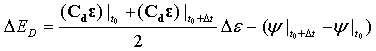
Viskoser Energieverbrauch:

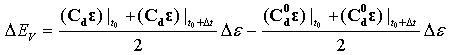
Referenzen:

1. Hashin, Z., A fatigue failure criterion for fiber reinforced materials, Journal of Composite Materials, 7 (1973), 448-464.
2. Lapczyk, I. and Hurtado, J.A., Progressive damage modeling in fiber-reinforced materials, Composites: Part A, 38 (2007), 2333-2341.
3. Iannucci, L. and Ankersen, J., An energy based damage model for thin laminated composites, Composites Science and Technology, 66 (2006), 934-951.
4. Maimi, P., Camanho, P.P., Mayugo, J.A., and Davila, C.G., A continuum damage model for composite laminates: Part I - constitutive model, Mechanics of Materials, 39 (2007), 897-908.
5. Maimi, P., Camanho, P.P., Mayugo, J.A., and Davila, C.G., A continuum damage model for composite laminates: Part II - computational implementation and validation, Mechanics of Materials, 39 (2007), 909-919.