Da es keinen einzelnen Wertesatz für die Kontaktparameter gibt, der eine genaue Lösung für alle Modelle bereithält, muss der Benutzer einen guten Überblick über die Funktionen der einzelnen Parameter haben, um einen geeigneten Wertesatz für das jeweilige Problem zu bestimmen.
Sie können die Kontaktparameter für jedes Paar einzeln anpassen. Wählen Sie das Kontaktpaar in der Strukturansicht aus, klicken Sie mit der rechten Maustaste, und wählen Sie Einstellungen. Oder klicken Sie im Hauptdialogfeld (Tabellenkalkulation) MES: Fläche-Fläche-Kontakt für dieses Paar auf die Spalte Parameter. Mit beiden Methoden wird das Dialogfeld Steuerungen und Parameter für Kontaktpaar aufgerufen. (Paare, deren Parameter geändert wurden, werden unter Benutzerdefiniert in der Spalte Parameter angezeigt. Andernfalls wird in der Spalte Parameter Standard angezeigt.)
Dialogfeld Steuerungen und Parameter für Kontaktpaar
Art des Kontaktproblems
Wählen Sie im Dropdown-Feld Art des Kontaktproblems den allgemeinen Kontakttyp, der während der Analyse jederzeit auftreten kann. Diese Auswahl steuert das Verhalten der automatischen Kontaktsteifheitsberechnung. In einigen Fällen ist die Auswahl eindeutig. In anderen Fällen ist es nicht eindeutig, ob es sich um eine geringe oder hohe Geschwindigkeit handelt. Der Unterschied ist von der Lösungseffizienz abhängig. Alle Auswahlmöglichkeiten sollten zu genauen Ergebnissen führen. Die verfügbaren Optionen lauten wie folgt:
- Langsamer Kontakt (Einpressen): Der Kontakt zwischen dem Paar ist dadurch gekennzeichnet, dass die Bauteile langsam zusammengefügt werden (geringe Geschwindigkeit) oder die Bauteile in ständigem Kontakt (Einpressen) sind. Die adaptive Kontaktsteifheit kann verwendet werden, wird vorgabemäßig jedoch nicht verwendet.
- Schneller Kontakt (Stoß): Der Kontakt zwischen dem Paar ist dadurch gekennzeichnet, dass eine schnelle Änderung auftritt, wie beispielsweise Aufprall- oder Fallversuche. Die adaptive Kontaktsteifheit wird nicht standardmäßig verwendet.
Kontaktmethode
Wählen Sie im Dropdown-Feld Kontaktmethode die Kontaktmethode aus, die für das ausgewählte Kontaktpaar verwendet werden soll. Die Optionen lauten wie folgt:
- Reibungsloser Kontakt: Mit dieser Kontaktmethode können Bauteile große relative Bewegungen zueinander an den Kontaktflächen aufweisen. Bauteile können während des gesamten Ereignisses in Berührung kommen. Keine Berührung kann ebenfalls während des Ereignisses auftreten. Die Bewegung zwischen den Flächen wird nicht durch Reibung behindert. Dies ist die häufigste Kontaktmethode.
- Reibungskontakt: Diese Kontaktmethode ist mit dem reibungslosen Kontakt identisch, mit der Ausnahme, dass Reibung so definiert werden kann, dass der Gleitbewegung zwischen den Flächen entgegengewirkt wird. Die Koeffizienten, die Sie definieren müssen, hängen von der Einstellung Reibungsgesetz ab, die Sie im Abschnitt Reibung modellieren angeben.
- Reibungsloses Gleitkontakt/Kein Kontaktprellen: Bei dieser Kontaktmethode können sich zwei Flächen frei bewegen, bis ein Kontakt auftritt. Die Knoten werden anschließend auch unter Spannung nicht getrennt. Die tangentiale Richtung kann separat mit Abhängigkeiten versehen werden. Verwenden Sie das Kontrollkästchen Kein Gleiten im Abschnitt Optionen Gleitkontakt/Kein Kontaktprellen, um zu verhindern, dass die Bauteile bei Berührung gleiten. In diesem Fall werden die sich berührenden Bauteile verbunden. Andernfalls können die Flächen frei aufeinander gleiten, wenn das Kontrollkästchen Kein Gleiten deaktiviert ist. Beachten Sie, dass die Flächen auseinandergleiten können, wenn die Option Kein Gleiten deaktiviert ist.
- Reibungsloses Gleitkontakt/Kein Kontaktprellen: Dieser Kontakttyp ähnelt dem oben beschriebenen Typ Gleitkontakt/Kein Kontaktprellen. Der Unterschied besteht darin, dass Reibung vorhanden ist, sobald sich die Flächen berühren. Statische Reibungskoeffizienten und Gleitreibungskoeffizienten können im Abschnitt Reibung modellieren festgelegt werden; siehe Reibungskontakt weiter oben für eine Beschreibung. Anmerkung: Das Kontrollkästchen keine Federkraft im Abschnitt Optionen Gleitkontakt/Kein Kontaktprellen ist immer aktiviert und kann nicht geändert werden. Die Beschränkung keine Federkraft kann nur angewendet werden, wenn eine oder zwei Kein Kontaktprellen-Optionen im Dropdown-Feld Kontaktmethode ausgewählt werden. Dieses Kontrollkästchen wird für die anderen Kontaktmethoden ignoriert.
- Verbundener Kontakt: Mit dieser Methode wird verbundener Kontakt zwischen Flächen, die nicht übereinstimmende Knoten enthalten, simuliert. Wenn diese Kontaktmethode ausgewählt wird und die Flächen zu Beginn in einer bestimmten Entfernung zueinander sind, werden die Flächen als dauerhaft verbunden betrachtet und während des Ereignisses nicht getrennt noch unter Spannung verschoben. Wenn der Abstand zwischen den Flächen größer ist als die angegebene Entfernung, wird der Kontakt nicht berücksichtigt. Der angegebene Abstand kann mithilfe des Abschnitts Verbundene Kontaktoptionen gesteuert werden. Wenn das Kontrollkästchen Verbundene Kontakt-Anfangsinterferenz nicht aktiviert ist, wird der ursprüngliche Abstand zwischen den Flächen als Kontaktabstand verwendet. Wenn dieses Kontrollkästchen aktiviert ist, muss der Abstand im Feld Verbundener Kontaktabstand angegeben werden. Eine Analyse, bei der diese Kontaktmethode verwendet wird, ist nicht so schnell wie eine Analyse, bei der die Knoten auf den Flächen übereinstimmen. Anmerkung: Nur die drei Translatoren der Knoten (Tx, Ty, Tz) auf den Flächen sind miteinander verbunden. Die Rotationen sind nicht verbunden. In einer Anordnung der Schalenelemente, die von der Fläche eines Quaderbauteils projiziert werden, beispielsweise ein Auslegerbalken aus Schalen, kann sich das Bauteil Schale frei an der Quader-Auflage drehen, wenn nur verbundener Kontakt zwischen der Schale und den Quadern verwendet wird.
Kontakttyp
Wählen Sie im Dropdown-Feld Kontakttyp den Kontakttyp aus, der für das ausgewählte Kontaktpaar verwendet werden soll.
Es ist etwas irreführend, Kontakt als Fläche-zu-Fläche zu beschreiben. In der Realität werden die Knoten auf dem zweiten Bauteil bzw. der zweiten Fläche mit der Fläche des ersten Bauteils bzw. der ersten Fläche verbunden. Dadurch wird verhindert, dass die Knoten durch die Fläche verlaufen. Optional trifft auch das Gegenteil zu: Die Knoten auf dem ersten Bauteil bzw. der ersten Fläche können mit der Fläche des zweiten Bauteils bzw. der zweiten Fläche verbunden werden. Auf keinen Fall wird verhindert, dass die Fläche eines Bauteils durch die Fläche des zweiten Bauteils verläuft.
Die Optionen für Kontakttyp sind wie folgt:
- Automatisch: Bei der Standardmethode wählt der Gleichungslöser basierend auf der Kontaktfläche (Netz) und dem Materialmodell zwischen den Kontakttypen Punkt zu Oberfläche und Oberfläche zu Oberfläche. Der Gleichungslöser bestimmt außerdem, welche Fläche als primäre Fläche verwendet wird. (Der Gleichungslöser wechselt möglicherweise zwischen dem ersten und zweiten Bauteil bzw. der ersten und zweiten Fläche, bevor die Analyse beginnt.) Die Option Automatisch wählt möglicherweise nicht den geeignetsten Kontakttyp aus, wenn große Verformungen in der Analyse vorkommen. Überprüfen Sie in diesem Fall die Gültigkeit der Einrichtung durch die Option Automatisch. Der ausgewählte Kontakttyp wird in der Protokolldatei aufgelistet (mit der Liste der Anzahl der Elemente in jedem Bauteil).
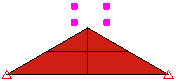
- Oberfläche zu Oberfläche: Diese Option gibt an, dass eine Berührung auftritt, wenn die Knoten auf dem sekundären Bauteil versuchen, durch die Fläche des primären Bauteils und umgekehrt zu verlaufen. Die Knoten auf dem primären Bauteil können die Fläche des sekundären Bauteils berühren.
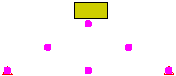
- Punkt zu Oberfläche: Diese Option gibt an, dass eine Berührung stattfindet, wenn die Knoten auf dem sekundären Bauteil versuchen, durch die Fläche des primären Bauteils zu verlaufen. Die Knoten auf dem primären Bauteil bzw. der primären Fläche können durch die sekundäre Fläche verlaufen.
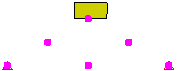
- Punkt zu Punkt: Diese Methode eignet sich am besten für Situationen, in denen die beiden Flächen kaum aufeinander gleiten. Diese Option gibt an, dass eine Berührung stattfindet, wenn die Knoten auf dem sekundären Bauteil versuchen, durch die Knoten auf dem primären Bauteil zu verlaufen. Die Berührung zwischen dem Knoten und der Fläche auf dem primären Bauteil wird nicht ermittelt. Unabhängig davon, wie die Bauteile verschoben werden, ist die Kontaktkraft immer zwischen dem ursprünglichen Paar der Knoten, die miteinander verbunden sind. Wenn der Kontakt Punkt zu Punkt erstellt wird, werden in der Ergebnisanzeige zusätzliche Bauteile im Modell angezeigt: ein Bauteil von Kontaktelementen für jedes Paar des Kontakts Punkt zu Punkt.
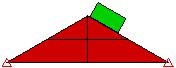
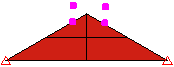
Die Methode Punkt zu Oberfläche ist schneller, Sie müssen sich jedoch bewusst sein, dass Punkte auf dem ersten Bauteil durch Flächen auf dem zweiten Bauteil verlaufen könnten. Dieser Kontakt wird nicht ermittelt. Fläche-Fläche-Kontakt bietet eine bessere Kontakterkennung, jedoch werden auch mehr Kontaktelemente erzeugt. Er gibt an, dass die Knoten auf dem Zielbauteil bzw. der Zielfläche nicht durch die Fläche verlaufen können, die durch die Knoten auf dem Hauptbauteil bzw. der Hauptfläche definiert ist (wie der Kontakt Punkt zu Oberfläche). Die Knoten auf dem Hauptbauteil bzw. der Hauptfläche können nicht durch die Fläche auf dem Zielbauteil bzw. der Zielfläche verlaufen. Siehe Abbildung 2.
|
Fläche-Fläche-Kontakt
|
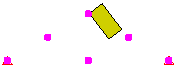
Punkt-zu-Fläche-Kontakt (Punkte auf dem Keil)
|
Punkt-zu-Fläche-Kontakt (Punkte auf dem Block)
|
|
Zeit = 0 |
||
|
Ersatzsystem. Die Flächen der beiden Bauteile sind durch Kontakt verbunden. |
Ersatzsystem. Nur die Knoten auf dem Keil sind vorhanden, was den Kontakt anbelangt. |
Ersatzsystem. Nur die Knoten auf dem Block sind vorhanden, was den Kontakt anbelangt. |
| Zeit = 0,024 Sekunden | ||
|
Die Fläche des Blocks kommt mit der Fläche bzw. dem Knoten des Keils in Berührung. |
Die Fläche des Blocks kommt mit dem Knoten des Keils in Berührung. |
Eine Berührung findet nicht statt, bis die Knoten des Blocks mit der Fläche des Keils in Berührung kommen. Der Keil verläuft durch den Block. |
| Zeit = 0,12 Sekunden | ||
|
Die Fläche des Blocks gleitet auf der Fläche des Keils hinunter. |
Der Block verläuft durch die Knoten des Keils. |
Der Block bleibt auf dem Keil haften. |
| Zeit = 0,15 Sekunden | ||
|
|
|
|
Abbildung 1: Vergleich von Kontakttypen Drei Modelle, bei denen ein Block auf einem Keil positioniert wird. Jedes Modell verwendet einen anderen Kontakttyp. |
||
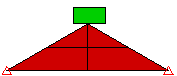
Wenn sich eine der Flächen im Kontaktpaar auf einem Bauteil der Schalenelemente befindet, wählen Sie die Seite der Schalen, die im Kontaktpaar vorhanden sein wird. (Die obere Seite ist die Seite gegenüber der Element-Knotennormale, die im Dialogfeld Elementdefinition festgelegt wird.) Eine Berührung findet nur dann statt, wenn sich die beiden Körper aus der angegebenen Richtung annähern. Beispiel: Wenn Sie angeben, dass eine Berührung mit der Oberseite der Schale stattfindet, dann findet eine Berührung mit dem zweiten Körper statt, der sich in der Richtung von oben nach unten bewegt. Kein Kontakt wird hergestellt, wenn sich der zweite Körper von unten nach oben bewegt. Eine andere Möglichkeit zur Visualisierung ist folgende: Das zweite Objekt stellt Kontakt mit der ausgewählten Seite (oben oder unten) nur her, wenn es sich von außerhalb der Schale annähert. Ein Kontakt wird nicht ermittelt, wenn es durch die Schale verläuft, um die gewählte Seite zu erreichen. Siehe Abbildung 3.
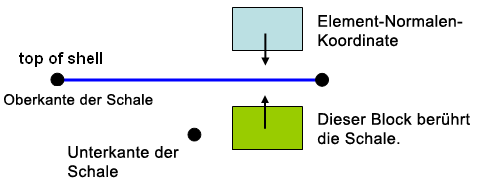
Abbildung 2: Zwei Blöcke, die für den Kontakt mit der Oberseite der Schale definiert sind
Kontakt mit Linienelementen (Balken, Stäbe) kann nur ermittelt werden, wenn die Knoten auf dem Linienelement die Fläche des ersten Bauteils bzw. der ersten Fläche berühren. Geben Sie zusätzlich an, ob alle Knoten auf den Linienelementen für den Kontakt berücksichtigt werden sollen (Alle im Zeilenelement) oder nur die Endknoten (Nur die an den Elementenden). Die Auswahl erfolgt im Dropdown-Feld In Kontakt stehende Knoten. Die Borsten auf einer Zahnbürste beispielsweise, die aus Balkenelementen bestehen, müssen nur einen Kontakt von den Knoten am Borstenende mit dem Zahn aufweisen. Folglich werden nur die Knoten an den Elementenden verwendet. Bei einem Sicherheitsnetz, das aus Stabelementen besteht, muss eine Berührung zwischen allen Knoten auf dem Netz und dem fallenden Objekt ermittelt werden. In diesem Fall wird die Option Alle im Zeilenelement verwendet.
Abschnitt Reibung modellieren
Bei reibungslosem Kontakt sind die Matrizen der Elementsteifheit symmetrisch. Wenn Reibung beteiligt ist, wird die Matrix asymmetrisch. Die Verwendung eines asymmetrischen Solvers ist in Bezug auf den Rechenaufwand teurer als die Verwendung eines symmetrischen Solvers. Aufgrund der Effizienz erfordert MES die Symmetrie der Elementsteifheit, sodass der symmetrische Solver für Reibungskontakt verwendet werden kann.
Wenn Reibungskontakt in der Analyse berücksichtigt wird, wird der Lösungsvorgang durch den Gleitvorgang sehr anfällig. Wenn die Kontaktflächen beginnen zu gleiten, ist der Gleichgewichtszustand vor der Gleitbewegung nicht mehr zulässig. Der Gleichungslöser muss während des Lösungsvorgangs einen neuen Gleichgewichtszustand finden. Darüber hinaus ist aufgrund der Symmetrieannäherung eine unzureichende Konvergenz möglich. Jede der verfügbaren Reibungsgesetzoptionen versucht, die Instabilität auf unterschiedliche Weise zu steuern.
In Simulation Mechanical stehen für den nicht linearen Fläche-Fläche-Kontakt drei Reibungsgesetz-Optionen zur Verfügung:
- Geänderte Coulomb-Reibung
- Coulomb mit viskose Reibung
- Geglättete Coulomb-Reibung
Jedes dieser Reibungsgesetze und die in diesem Zusammenhang angewendeten Parameter werden in den folgenden Unterabschnitten erörtert.
Geänderte Coulomb-Reibung
Dieses Reibungsgesetz verwendet den klassischen Reibungsalgorithmus: Coulomb-Reibung. Im grundlegenden Modell der Coulomb-Reibung können zwei Kontaktflächen der Scherspannung bis zu einer bestimmten Menge entgegenwirken, die anhand von Reibungskoeffizienten und normalem Kontaktdruck festgelegt wurde, bevor relative Gleitbewegungen auftreten. Das Modell der Coulomb-Reibung wird als τ = μP definiert, wobei μ der Reibungskoeffizient und P der normale Kontaktdruck ist. Der Fläche-Fläche-Kontakt bietet die Möglichkeit zum Definieren eines statischen Reibungskoeffizienten μs und eines dynamischen Reibungskoeffizienten μd. Sobald die Scherspannung μsP überschreitet, die aus der Eingabe Statischer Reibungskoeffizient resultiert, beginnen die beiden Flächen im besten Fall an zu gleiten. Darüber hinaus wird die Scherspannung zu μdP, wobei der Gleitreibungskoeffizient-Wert verwendet wird.
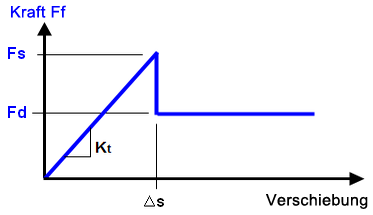
Die ideale Situation (keine Bewegung, bis die Scherspannung den statischen Wert überschreitet) ist numerisch schwierig zu erreichen, wie in Abbildung 3 beschrieben. Folglich wird ein Tangentiales Steifigkeitsverhältnis festgelegt, wenn dieses Reibungsgesetzt verwendet wird. Das tangentiale Steifigkeitsverhältnis ist das Verhältnis der tangentialen Kontaktsteifheit (Kt) zur Kontaktsteifheit in der Normalrichtung (K), das über die Schaltfläche Erweitert festgelegt wird. Siehe Seite Erweiterte Steuerelemente für Fläche-Fläche-Kontakt.) Eine größere tangentiale Steifigkeit führt zu einer besseren Genauigkeit, jedoch sind mehr Wiederholungen erforderlich. Eine geringere tangentiale Steifigkeit bietet bessere Konvergenz (kürzere Laufzeit) mit reduzierter Genauigkeit. Der empfohlene Wert liegt in einem Bereich von 0,01 bis 1 und der Standardwert lautet 0,01. Wenn der statische Reibungskoeffizient größer wird, ist ein geringeres tangentiales Steifigkeitsverhältnis ratsam.
|
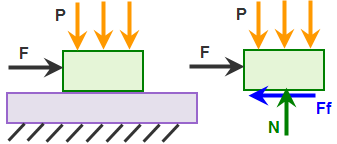
(a) Abbildung des Modells und freien Körpers für den oberen Block. Die angewendete Kraft F wird mit der Zeit erhöht, bis sie die Haftreibung überschreitet. |
|
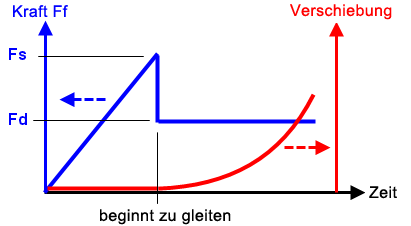
(b) Plot der Reibungskraft Ff vs. Zeit (blaue Kurve) und Verschiebung vs. Zeit (rote Kurve). Bis die Reibungskraft Ff die Grenze der Haftreibung erreicht (Fs = μs * N), gibt es keine Bewegung des Bauteils. Nachdem die Haftreibung überschritten wurde, fällt die Reibungskraft Ff von Fs auf Fd (= μd * N), und das Bauteil beginnt zu beschleunigen. |
|
(c) Die Diagramme in Abbildung (b) werden kombiniert, um die Reibungskraft vs. Verschiebung zu zeigen. Im Idealfall gibt es keine Verschiebung, bis die Reibungskraft Fs erreicht, und die Gleitbewegung beginnt. Numerisch ist dies schwierig zu erreichen, da jede von Null verschiedene Verschiebung eine Reibungskraft von Fd beinhaltet. |
|
(d) Um die numerische Instabilität in Abbildung (c) zu vermeiden, kann das Bauteil etwas verschoben werden (Δs), während die Reibungskraft kleiner ist als die Haftreibungsgrenze (Fs). Die Bewegung wird durch die tangentiale Steifigkeit (Kt = Fs/Δs) gesteuert. Durch kleinere Kt-Werte kann das Bauteil weiter verschoben werden, bevor die Gleitbewegung einsetzt. Außerdem ist das Konvergieren einfacher, während höhere Kt-Werte (stärkere Neigung) geringere Verschiebungen ermöglichen, bevor die Gleitbewegung einsetzt. Sie führen außerdem zu erschwertem Konvergieren. Die tangentiale Steifigkeit wird anhand des tangentialen Steifigkeitsverhältnisses x Steifigkeit in der Normalrichtung berechnet. |
| Abbildung 3: Tangentiale Steifigkeit für geänderte Coulomb-Reibung |
Coulomb mit viskose Reibung
Im Gegensatz zu dem geänderten Coulomb-Reibungsgesetz werden statische und dynamische Reibungskoeffizienten im Coulomb mit viskose Reibungsgesetz nicht berücksichtigt. Im geänderten Coulomb-Reibungsgesetz ist eine relativ hohe Kraft erforderlich, um statische Reibung zu überwinden und Bewegung zu starten. Sobald die Reibung beginnt, nimmt die Reibungskraft ab , da der Gleitreibungskoeffizient kleiner als der statische Koeffizient ist. Daher tritt eine Kraftdiskontinuität aufgrund der abrupten Änderung in der Reibungskraft auf. Für das Coulomb mit viskose Reibungsgesetz gibt es keine Reibungskraftdiskontinuität, wenn das Gleiten beginnt. Stattdessen wird die Reibungskraft beim Erhöhen der Geschwindigkeit allmählich erhöht .
Für die Option Coulomb mit viskose Reibung müssen Sie zwei Parameter definieren:
- Gleitreibungskoeffizient (Fd): Dies wird auch als dynamischer Reibungskoeffizient bezeichnet. Es ist das Verhältnis der tangentialen Kraft, die notwendig ist, um die relative Bewegung und die normale Kraft zwischen den sich berührenden Bauteilen beizubehalten. Beispiel: Wenn 15N tangentialer Kraft erforderlich sind, um einen Block entlang eines angrenzenden Bauteils beizubehalten, und die normale Kontaktkraft dazwischen 100N beträgt, lautet der Gleitreibungskoeffizient 15N / 100N = 0,15. In Anbetracht dieses Reibungsgesetzes sollten Sie die Gleitgeschwindigkeit für den Gleitreibungskoeffizienten relativ gering halten.
- Viskose Reibungskoeffizient (νs): Dies ist die Neigung der Reibungskraft im Vergleich zur Schiebegeschwindigkeitskurve. Für alle viskose Effekte gilt, dass die Kraft, die zur Überwindung der viskosen Effekte notwendig ist, proportional zur Geschwindigkeit ist.
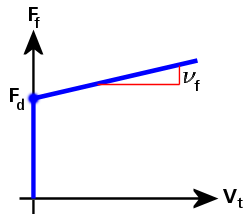
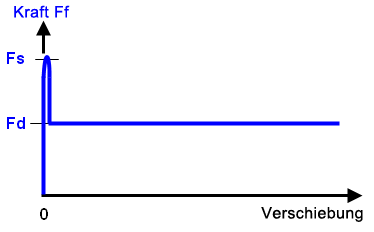
Abbildung 4: Reibungskraft im Vergleich zur Schiebegeschwindigkeit (Coulomb mit viskose Reibung )
In Abbildung 4 wird die Kurve für die Reibungskraft (Ff) wie folgt definiert:
Ff = Fd + νf · Vt
Dabei gilt:
Fd ist die dynamische (gleitende) Reibungskraft,
νf ist der viskose Reibungskoeffizient und
Vt ist die tangentiale (gleitende) Geschwindigkeit zwischen den beiden Bauteilen.
Wenn νf = 0 ist, ist Ff = Fd
Geglättete Coulomb-Reibung
Wie die Coulomb mit viskose Reibung , berücksichtigt auch die Geglättete Coulomb-Reibung nur den Gleitreibungskoeffizienten. Auf diese Weise scheidet die Diskontinuität der Reibungskraft zwischen den statischen und gleitenden Bedingungen bei Verwendung des Ändern der Coulomb-Reibung-Gesetzes aus. Der Übergang zwischen statischen und gleitenden Bedingungen wird zudem durch die Integration eines gleichmäßigen Übergangsfaktors (Φ) stabilisiert.
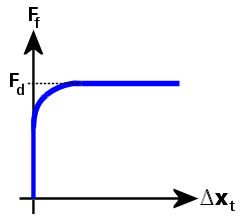
Abbildung 5: Reibungskraft im Vergleich zur tangentialen relativen Verschiebung (geglättete Coulomb-Reibung)
In Abbildung 5 wird die Kurve für die Reibungskraft (Ff) wie folgt definiert:
Ff = Fd · Φ, und
Φ = tanh(3 · Δxt / δ)
Dabei gilt:
Fd ist die dynamische (gleitende) Reibungskraft.
Φ ist ein Übergangsfaktor, der die Reibungskraft gleichmäßig bis null gleiten lässt, wenn die tangentiale relative Verschiebung null erreicht. In ähnlicher Weise gleitet die Reibungskraft gleichmäßig bis zur dynamischen Reibungskraft, wenn sich die tangentiale relative Verschiebung erhöht.
Δxt ist die tangentiale relative Verschiebung und
δ ist eine Toleranz, die basierend auf der Kontaktsteifheit und dynamischen Reibungskraft berechnet wird.