Stabelemente sind Zwei-Knoten-Elemente, die eine beliebige Ausrichtung im XYZ-System aufweisen können. Der Stab überträgt nur Axialkraft und ist im Allgemeinen ein Element mit drei Freiheitsgraden (FHG). Mit Stäben werden Strukturen wie Masten, Brücken und Gebäude modelliert.
Es wird davon ausgegangen, dass das dreidimensionale (3D) Stabelement einen konstanten Querschnittsbereich hat und in linear-elastischen Analysen verwendet werden kann. Linear-elastisches Materialverhalten wird nur durch das Elastizitätsmodul definiert. Lineare Stäbe können auch zur Simulation von Translations- und Verschiebungselementen verwendet werden.
Definitionsgemäß können Stäbe keine Rotations-Freiheitsgrade haben, selbst wenn Sie diese Freiheitsgrade beim Anwenden der Randbedingungen freigeben. Sie können Translations-Freiheitsgrade nach Bedarf anwenden.
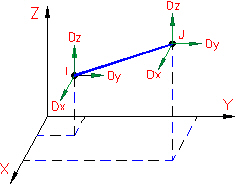
Abbildung 1: Formulierung eines Stabelements
Anwenden von Stabelementen
- Die Länge des Elements ist deutlich größer als die Breite oder Tiefe (ca. 8-10 mal).
- Es ist durch Scharniere, die keine Momente übertragen, mit dem übrigen Modell verbunden.
- Die externen angewendeten Kräfte wirken nur an Gelenken.
Parameter von Stabelementen
Geben Sie den Querschnittsbereich für die einzelnen Stabelementteile im Feld Querschnittsbereich im Dialogfeld Elementdefinition an. Dieser Wert muss größer als null sein und ist für eine Analyse erforderlich. Wenn Sie für dieses Bauteil eine thermische Spannungsanalyse durchführen, geben Sie im Feld Spannungsfreie Referenztemperatur die Temperatur ein, bei der die Elemente in diesem Bauteil keine wärmebedingten Spannungen aufweisen. Elementbasierte Lasten, die mit einer Abhängigkeit der Wärmeausdehnung in Zusammenhang stehen, werden anhand des Durchschnitts der auf den Knotenpunkt-Datenlinien angegebenen Temperaturen berechnet. Die Referenztemperatur dient zum Berechnen der Temperaturänderung. Die thermische Last kann zum Abrufen anderer Elementlasttypen verwendet werden. In diesen Fällen wird eine entsprechende Temperaturänderung (dT) verwendet.
So verwenden Sie Stabelemente
- Vergewissern Sie sich, dass ein Einheitensystem definiert ist.
- Vergewissern Sie sich, dass das Modell einen Strukturanalysetyp verwendet.
- Klicken Sie mit der rechten Maustaste auf die Überschrift Elementtyp für das Bauteil, das in Stabelemente verwandelt werden soll.
- Wählen Sie den Befehl Stab.
- Klicken Sie mit der rechten Maustaste auf die Überschrift Elementdefinition für das Bauteil, das in Stabelemente verwandelt werden soll.
- Wählen Sie den Befehl Elementdefinition bearbeiten.
- Geben Sie im Dialogfeld Elementdefinition einen Wert in das Feld Querschnittsbereich ein.
- Wenn Sie eine thermische Spannungsanalyse durchführen, geben Sie im Feld Spannungsfreie Referenztemperatur einen Wert an. Dies ist die Temperatur, bei der keine Spannungen im Modell vorhanden sind. Der Unterschied zwischen dieser Temperatur und den Knotentemperaturen erzeugt die Spannung.
- Klicken Sie auf OK.
Verwenden von Stabelementen zum Modellieren eines anfänglichen Lack-of-Fit
Die folgenden Gleichungen können für die Berechnung der entsprechenden Temperaturänderung verwendet werden, die mit einem anfänglichen Lack-of-Fit eines Stabelements zwischen zwei Punkten auftritt. Ein positiver Wert bedeutet, dass das Element zunächst zu kurz ist.
![]()
Dabei gilt:
![]()
Dabei gilt:
T avg = die durchschnittliche Knotentemperatur der beiden Knoten des Stabelements
T sf = die spannungsfreie Referenztemperatur des Bauteils
D = die Verlängerung oder Verkürzung des Stabelements
α = der thermische Ausdehnungskoeffizient des Bauteils
L = die unbelastete Länge des Stabelements
Verwenden von Stabelementen zum Modellieren einer anfänglichen Vorspannung
Die folgenden Gleichungen können für die Berechnung der entsprechenden Temperaturänderung verwendet werden, die mit einer anfänglichen Vorspannung verbunden sind, die zum Verschieben eines Stabelements für die Einpassung zwischen zwei Punkten verwendet wird.
![]()
Dabei gilt:
![]()
Dabei gilt:
T avg = die durchschnittliche Knotentemperatur der beiden Knoten des Stabelements
T sf = die spannungsfreie Referenztemperatur des Bauteils
P = die Axialkraft im Stabelement
E = das Elastizitätsmodul des Stabelements
A = der Querschnittsbereich des Stabelements
α = der thermische Ausdehnungskoeffizient des Bauteils
Die Kraft P ist die Anfangskraft im Stabelement, wenn die übrige Struktur keine Kraft aufweist. Wenn die übrige Struktur unendlich steif ist, dann ist das Ergebnis der Analyse eine Axialkraft P im beheizten Stabelement. Da die Struktur nicht unendlich steif ist, besteht ein Ergebnis der Vorspannung darin, dass sich die Struktur verbiegt und einen Teil der thermischen Vorspannung freistellt. Wenn Sie möchten, dass die Last P die endgültige Last im Stab darstellt (nachdem die Struktur aufgrund der Vorspannung verformt wurde), finden Sie Angaben zur Methode auf der Seite Balkenvorspannungen.