Verwenden Sie Analyse
Analyse Optimierung im FEM-Editor oder der Ergebnisanzeige, um das Dialogfeld Entwurfsoptimierung zu öffnen. Die Registerkarte Parameter wird nur verwendet, um die Lösungsparameter für die Entwurfsoptimierung anzugeben; die Werte auf dieser Registerkarte haben keine Auswirkung auf eine Entwurfsstudie.
Die Optimierungsmethode legt den Algorithmus für die Entwurfsoptimierung fest. Die Optionen lauten wie folgt:
- SLP: Verwendet die sequentielle lineare Programmiermethode zum Lösen der Analyse. Zuerst wird eine Taylor-Näherung (linear) für die Ziel- und Beschränkungsfunktionen erstellt. Diese Näherung wird verwendet, um die optimale Lösung zu finden. Diese Methode ist die zuverlässigste Lösungsmethode.
- SQP: Verwendet eine sequenzielle quadratische Programmiermethode zum Lösen der Analyse. Zuerst wird eine Taylor-Näherung (quadratisch) für die Zielfunktionen erstellt. Eine lineare Näherung der Abhängigkeitsfunktionen wird erstellt. Diese Näherungen werden verwendet, um die optimale Lösung zu finden. Diese Methode ist schneller als SLP, jedoch nicht immer so stabil.
- Antwortfläche: erstellt eine globale Funktion, die das Verhalten der Modellantwort auf die Änderung der Entwurfsvariablen darstellt. Da die Funktion ein größeres Intervall abdeckt, ist sie weniger detailliert als die SLP- oder die SQP-Methode. Daher kann der optimierte Wert, der mit der Antwortflächen-Methode gefunden wird, nur eine Näherung des tatsächlichen optimierten Wertes sein. Für eine genauere Lösung führen Sie die Antwortfläche aus, um dem optimierten Wert näher zu kommen. Verwenden Sie dann die SLP- oder die SQP-Methode mit Eingaben basierend auf den Antwortflächenergebnissen.
Beachten Sie, dass die absolut optimale Lösung nur garantiert ist, wenn das Ziel konvex (bei Suchen des Minimums) bzw. konkav ist (bei Suchen des Maximums), innerhalb des Entwurfsbereichs von der Unter- bis zur Obergrenze der einzelnen Entwurfsvariablen. Wenn die Optimierungskurve Biegungen hat, dann kann ein lokales optimales Ergebnis gefunden werden; mit einer anderen Optimierungsmethode oder Anpassung der Unter- und Obergrenzen kann ein anderes optimales Ergebnis gefunden werden. In Abbildung 1 ist ein Beispiel dargestellt.
|
Ziel/Abhängigkeiten Entwurfsbereich (a) die theoretische Kurve der Ziel/Abhängigkeitsgleichung. Der Mindestwert ist klar, wenn die Kurve bekannt ist, er ist aber nicht im Voraus bekannt. Mit numerischen Methoden wird die Kurve berechnet und versucht, den Mindestwert mit dem geringsten Berechnungsaufwand zu finden. |
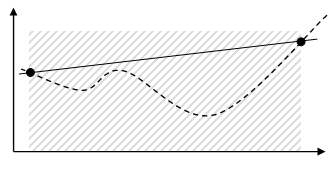 (b) Mit der SLP-Methode wird die Kurve an der Ober- und Untergrenze des Entwurfsbereichs ausgewertet. Da die Untergrenze das Minimum ist, beginnt die Liniensuche an der Untergrenze. |
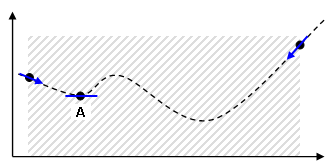 (c) Anhand verschiedener Parameter sucht die Suchroutine ein Minimum an Punkt A der theoretischen Kurve. Nachdem ein Minimum gefunden wurde, ist die Lösung konvergiert. Es handelt sich nicht um das absolute Minimum, sondern um ein lokales Minimum. |
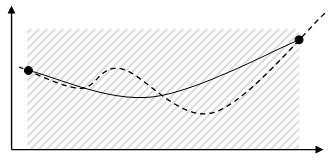 (d) Mit der SQP-Methode wird eine quadratische Gleichung verwendet, um die theoretische Kurve zu schätzen. |
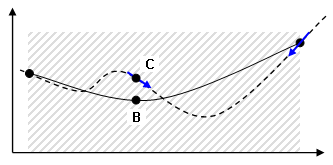 (e) Das Minimum der quadratische Gleichung erfolgt bei B. Bei diesem Wert der Entwurfsvariablen liegt die theoretische Kurve bei C und verfügt über eine berechnete Neigung. |
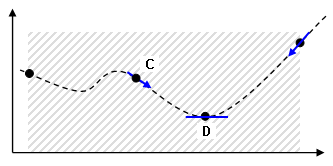 (f) Die Suchroutine verwendet verschiedene Parameter, um einen Minimumpunkt D auf der theoretischen Kurve zu finden. Nachdem ein Minimum gefunden wurde, ist die Lösung konvergiert. |
| Abbildung 1: Erläuterndes Beispiel für die Suche des Minimums |
Entwurfsvariablen Zu Abbildung 1 sind noch einige weitere Anmerkungen erforderlich.
- Die Suchrichtung und die Bewegungsgrenzen sind stärker von den Unter- und Obergrenzen betroffen, wenn Sie die SLP-Methode verwenden, als bei der SQP-Methode.
- Für die Erfüllung Abhängigkeiten (obere und untere Grenzwerte für Spannung, Verformung usw.) kann am durch die obigen Methoden optimierten Wert nicht garantiert werden. Nachdem der Punkt der 0-Neigung gefunden ist (der optimale Wert), kann die Routine nicht mehr entscheiden, wohin sie gehen soll, wenn eine Abhängigkeit verletzt wird. In solchen Situationen kann der Bereich der verletzten Entwurfsvariablen angepasst und die Optimierungsanalyse wiederholt werden.
Das Feld Maximale Iterationen gibt die Anzahl der Iterationen an, die während der Optimierung verwendet werden. Wenn die Lösung nicht innerhalb der Anzahl der Iterationen gefunden wird, dann wird die Entwurfsoptimierung beendet. Prüfen Sie immer die Protokolldatei nach Abschluss der Analyse, um zu sehen, wie nahe die Abhängigkeiten dem festgelegten Grenzwert kamen.
Bedenken Sie, dass die vollständige Optimierungsanalyse die Analyse für ein Vielfaches der angegebenen Anzahl Iterationen durchführen könnte. Wenn eine normale Analyse eine halbe Stunde dauert und Sie 20 Iterationen angeben, dann kann die gesamte Optimierung mindestens 10 Stunden dauern, und möglicherweise 60 bis 100 Stunden (je nach der Anzahl der Entwurfsvariablen und wie viele Iterationen für die Konvergenz erforderlich sind).
Das Feld Maximale Zieländerung bestimmt, wann die Lösung zur Antwort konvergiert ist. Es handelt sich um eine Toleranz. Wenn die Änderung an den einzelnen Abhängigkeitswerten (eine Ziel/Abhängigkeit, die auf der Registerkarte Leistung angegeben wird) von einer Iteration zur nächsten innerhalb des Bereichs des aktuellen Ergebnisses mal Toleranz liegt, dann ist die Lösung konvergiert. (Mathematisch betrachtet -Toleranz <= (aktuelles Ergebnis - vorheriges Ergebnis)/aktuelles Ergebnis <= +Toleranz.)