Tetraederelemente

Lineare Tetraederelemente sind entweder konstante Spannungselemente mit vier Knoten oder lineare Spannungselemente mit 10 Knoten. Diese Elemente werden im dreidimensionalen Raum mit drei Freiheitsgraden pro Knoten formuliert; diese sind die Freiheitsgrade der Verschiebung in den Richtungen X, Y und Z. Das 10-Knoten-Element ist ein isoparametrisches Element und Spannungen werden an den Knoten berechnet. Die folgenden elementbasierten Lasten können angewendet werden:

1. Einheitlicher oder hydrostatischer Druck auf die Flächen des Elements.
2. Thermische Verläufe, definiert durch die Temperaturen am Knoten.
3. Einheitliche Trägheitslast in drei Richtungen.

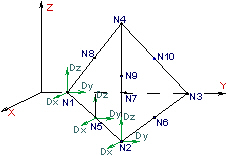
Abbildung 1: Tetraederelement mit 10 Knoten

Bestimmung der Flächennummer für Tetraeder

Beachten Sie beim Anwenden von Lasten auf eine Flächennummer eines Tetraederbauteils, dass einige Modelle nicht alle Linien auf der Fläche zum Laden auf der gleichen Flächennummer haben. Was geschieht in dieser Situation? Wenn das Modell aus einem CAD-Volumenkörpermodell stammt, erhalten alle Flächen, die mit der Oberfläche des CAD-Modells übereinstimmen, die Last, unabhängig von der Flächennummer der Linien. In manuell erstellten Modellen und auf CAD-Bauteilen, die so geändert wurden, dass das Bauteil nicht mehr mit dem CAD-Bauteil verknüpft ist, definiert die Flächennummer, die zwei der drei Linien einer Flächendefinition gemeinsam haben, die Flächennummer dieser Fläche.

Tetraederelemente können laut Definition keine Rotations-Freiheitsgrade haben, selbst wenn Sie diese Freiheitsgrade beim Anwenden der Randbedingungen freigegeben haben. Sie können translatorische Freiheitsgrade nach Bedarf anwenden.

Verwendung von Tetraederelementen

• Die Spannungsergebnisse durch die Dicke eines Bauteils wird bevorzugt.
• Das Modell hat nur angewendete Kräfte, keine Momente. (Tetraeder haben keine Rotations-Freiheitsgrade). Informationen zum Anwenden eines Moments auf ein Tetraederelement finden Sie auf der Seite Fehlerbehebung: Kontaktbeispiele.
• Auf das Modell wurde ein hydrostatischer Druck oder eine Druckbelastung angewendet.

Tetraederelementparameter

Wenn Sie möchten, dass für die Tetraederelemente in diesem Bauteil die Mittelknoten aktiviert werden, wählen Sie die Option Einbezogen im Dropdown-Menü Mittelknoten aus. Wenn diese Option ausgewählt ist, haben die Tetraederelemente zusätzliche Knoten in der Mitte jeder Kante definiert. (Bei Netzen von CAD-Volumenkörpermodellen folgen mittlere Knoten der ursprünglichen Krümmung der CAD-Oberfläche, abhängig von der gewählten Option, bevor das Netz erstellt wurde. Bei handgefertigten Modellen und geänderten CAD-Modellnetzen befindet sich der mittlere Knoten in der Mitte zwischen Eckknoten.) Dadurch wird ein Tetraederelement mit 4 Knoten in ein Tetraederelement mit 10 Knoten geändert. Ein Element mit Mittelknoten führt zu genauer berechneten Verläufen. Dies ist besonders nützlich, wenn Sie versuchen, das Biegeverhalten mit einigen Elementen auf der Biegeebene zu modellieren. Elemente mit mittleren Knoten verlängern die Verarbeitungszeit. Wenn das Netz ausreichend klein ist, wird mit den Mittelknoten u. U. kein wesentlich genaueres Ergebnis erzielt.

Tipp: Die Verschiebung an den Mittelknoten ist immer eine Ausgabe. Die Spannung und Dehnung an Mittelknoten wird nur ausgegeben, wenn Sie die Option für die Ausgabe dieser Ergebnisse vor dem Ausführen der Analyse aktivieren. Die Option befindet sich im Dialogfeld Setup Modell einrichten Parameter. (Die Position der Analyseparameter variiert von Analysetyp zu Analysetyp.)

Wählen Sie als Nächstes den Integrationsgrad für die Tetraederelemente in diesem Bauteil in der Dropdown-Liste Integrationgrad aus. Für rechteckig geformte Elemente wählen Sie die Option zweitrangig aus. Für leicht verformte Elemente wählen Sie die Option3. Ordnung. Für extrem verformte Elemente wählen Sie die Option 4. Ordnung. Die Berechnungszeit für die Formulierung der Elementsteifigkeit erhöht sich mit der dritten Potenz der Integrationsreihenfolge. Aus diesem Grund sollte der niedrigste Integrationsgrad, der zu akzeptablen Ergebnissen führt, verwendet werden, um die Verarbeitungszeit zu verkürzen.

Wenn Sie eine thermische Spannungsanalyse für dieses Bauteil durchführen, geben Sie die Temperatur ein, bei der die Elemente in diesem Bauteil keine thermisch ausgelösten Spannungen erfahren, im Feld Spannungsfreie Referenztemperatur ein. Elementbasierte Lasten, die mit der Abhängigkeit temperaturabhängiges Wachstum verknüpft sind, werden anhand der Durchschnittstemperaturen berechnet, die für die Datenlinien der Knotenpunkte angegeben sind. Die Referenztemperatur dient zum Berechnen der Temperaturänderung. Die thermische Last kann zum Abrufen anderer Elementlasttypen verwendet werden. In diesen Fällen wird eine entsprechende Temperaturänderung (dT) verwendet.

So verwenden Sie Tetraederelemente

1. Vergewissern Sie sich, dass eine Systemeinheit definiert ist.
2. Vergewissern Sie sich, dass das Modell einen Strukturanalysetyp verwendet.
3. Klicken Sie mit der rechten Maustaste auf die Überschrift Elementtyp für das Bauteil, das als Tetraederelement dienen soll.
4. Klicken Sie auf den Befehl Tetraeder.
5. Klicken Sie mit der rechten Maustaste auf die Überschrift Elementdefinition.
6. Wählen Sie den Befehl Elementdefinition bearbeiten.
7. Um Mittelknoten in diesem Bauteil zu verwenden, wählen Sie die Option Einbezogen in der Dropdown-Liste Mittelknoten aus.
8. Wenn Sie eine thermische Spannungsanalyse durchführen, geben Sie eine Temperatur in das Feld Spannungsfreie Referenztemperatur ein. Der Unterschied zwischen diesem Wert und den angewendeten Temperaturen wird zum Berechnen der Spannung verwendet.