Das Duncan-Chang Materialmodell wird zur Simulation von Erdreich verwendet. Es setzt voraus, dass eine hyperbolische Spannungs-Dehnungs-Beziehung vorhanden ist, und wurde basierend auf tri-axialen Bodentests entwickelt. Während das ursprüngliche Modell einen konstanten Poisson-Koeffizienten voraussetzt (Duncan und Chang, 1970), enthält das überarbeitete Modell die Abweichung des Poisson-Koeffizienten durch einen spannungsabhängigen Poisson-Koeffizienen (E-v-Modell, Kulhawy und Duncan 1972) oder ein spannungsabhängiges Massenmodul (E-B-Modell, Duncan et al. 1980).
Formulierung:
Basierend auf standardmäßigen tri-axialen Bodentests nähert sich das Modell der Spannung/Dehnung durch das folgende hyperbolische Verhältnis:
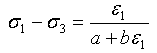 (1)
(1)
Dabei gilt: σ1 und σ3 sind die maximale und minimale Hauptspannung; ε1 ist die maximale Hauptdehnung (axiale Dehnung). Sie sollten beachten, dass wir die Symbolkonventionen in Bodenmechanik befolgen, im Gegensatz zur Kontinuum-Mechanik. Konstanten a und b sind aus den Testdaten kalibriert und können wie folgt geschrieben werden:
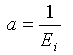 (2)
(2)
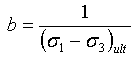
Dabei gilt: Ei ist das Anfangs-Tangentenmodul und (σ1-σ3)ult ist der asymptomatische Wert der hyperbolischen Kurve und ist durch das Fehlerverhältnis mit der Bodenstärke verbunden:
(σ1 - σ3)f = Rf(σ1 - σ3)ult (3)
Wie Sie sehen, ist das Fehlerverhältnis Rf immer kleiner als 1 und wurde zwischen 0.75 und 1 festgestellt (Duncan und Chang 1970).
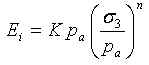 (4)
(4)
Das Duncan-Chang-Modell definiert das Anfangsmodul wie folgt:
Dabei gilt: Modul K und der Modulexponent n sind dimensionslose Materialparameter; pa ist der atmosphärische Druck, der in der Formel zur Eliminierung der Einheitensystemauswahl verwendet wird.
Der Bodenfehler wird durch das Mohr-Coulomb-Kriterium bestimmt:
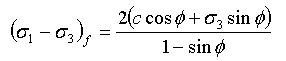 (5)
(5)
Dabei sind c und φ Mohr-Coulomb-Stärkeparameter. Für kohäsionsloses Erdreich sind die Mohr-Hüllen in der Regel gekrümmt und die Abweichung kann in dieser Form ausgedrückt werden:
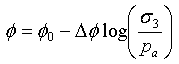 (6)
(6)
Dabei gilt: φ0 ist der Reibungswinkel beim atmosphärischen Druck des Begrenzungsdrucks σ3, und Δφ0 ist die Reduzierung in φ für eine 10-fache Erhöhung in σ3.
In der inkrementellen Form kann das tangentiale Modul folgendermaßen ausgedrückt werden:
Et = (1-RfS)2Ei (7)
Dabei gilt: S ist die Spannungsebene oder der Teil der mobilisierten Stärke:
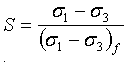 (8)
(8)
Wenn (σ1-σ) kleiner ist als das bisherige Maximum, wird davon ausgegangen, dass der Boden entlastet oder erneut belastet wird, und das tangentiale Modul wird wie folgt definiert:
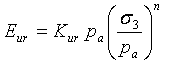 (9)
(9)
Dabei gilt: Kur ist die Entlastung/Neubelastung-Modulzahl und ist immer größer als die primäre Lastmodulzahl K. Der Modulexponent für Entlastung/Neubelastung ist derselbe wie in der primären Belastung.
Genauso kann auch im E-v-Modell (Kulhawy und Duncan 1972) der anfängliche Poisson-Koeffizient wie folgt ausgedrückt werden:
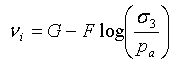 (10)
(10)
und der tangentiale Poisson-Koeffizient
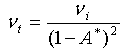 (11)
(11)
Dabei gilt:
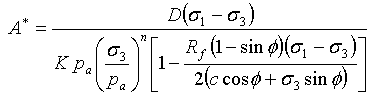 (12)
(12)
und D, F und G sind Materialparameter.
Im E-B-Modell (Duncan et al. 1980) wird das Massenmodul wie folgt ausgedrückt:
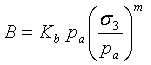 (13)
(13)
Dabei gilt: Kb und m sind jeweils Zahl und Exponent des Massenmoduls.
Ausgangsspannung:
Normalerweise ist es wichtig, den anfänglichen Spannungszustand für einen Bodenkörper zu beachten. Die Software bietet derzeit zwei Arten von Ausgangsspannungszuständen, abgeleitet aus einheitlichem hydrostatischem Druck und Eigengewicht. Für diese Ausgangsspannungen wird ein statisches Gleichgewicht vorausgesetzt, daher tragen sie nicht zu Spannungs- und Verformungswerten in der Analyse bei, die durch die äußeren angewendeten Lasten verursacht werden. Anders gesagt, die Ausgangsspannung ändert nicht die in der Ergebnisanzeige dargestellten Spannungsergebnisse, und sie bewirkt auch keine anfängliche Verschiebung. Wenn diese Annahme nicht zutrifft, simulieren Sie explizit den Belastungsverlauf.
Stabilisierung:
Während Sie sich in einem standardmäßigen tri-axialen Komprimierungstest befinden, ist der Begrenzungsdruck (σ3) immer größer als Null. Bei allgemeinen endlichen Elementanalysen kann er jedoch gleich oder kleiner als Null sein. Um eine numerisch stabile Analyse zu erhalten, ist für diesen Fall ein Satz anfänglicher E-Module erforderlich. Der Benutzer kann den Wert auf der Registerkarte Erweitert der Materialeigenschaften angeben (Youngs-Modul und Poisson-Koeffizient beim Rest). Wenn sie nicht bereitgestellt werden, wird die Standardeinstellung E0=0.01K*pa und ν0=0.499 verwendet.
Nach dem Fehlschlagen (die Spannungsebene erreicht 1) verliert der Boden effektiv seine Belastungskapazität. Ein Satz von Restmodulen ist für eine stabile Analyse erforderlich. Der Benutzer kann den Wert auf der Registerkarte Erweitert angeben (Youngs-Modul und Poisson-Koeffizient bei Versagen). Wenn sie nicht bereitgestellt werden, wird die Standardeinstellung E1=0.001K*paund ν1=0.499 verwendet. Dieser Wertesatz wird auch als Untergrenze für die E-Module vor dem Versagen verwendet.
Die Simulationsergebnisse können manchmal erheblich durch die oben genannten Stabilisierungsmodule beeinträchtigt werden. Während die E-Module beim Rest experimentell bestimmt werden können, ist es normalerweise schwer, ein geeignetes Fehlermodul für das Duncan-Chang-Modell zu bestimmen. Sie sollten jedoch beachten, dass das Duncan-Chang-Modell vor dem Versagen verwendet werden sollte und möglicherweise akzeptabel sein kann, wenn das Versagen eingeschränkt und lokalisiert ist.
Einschränkungen:
Das Duncan-Chang-Modell ist erfolgreich beim Berechnen vieler praktischer Probleme und kann einfach mit standardmäßigen tri-axialen Komprimierungstests eingerichtet werden. Wenn keine tri-axialen Testergebnisse verfügbar sind, sind auch in der Literatur zahlreiche Modellparameter verfügbar. Benutzer sollten jedoch wichtige Einschränkungen beachten (Duncan et al. 1980):
- Die mittlere Hauptspannung σ2 wird nicht berücksichtigt.
- Die Ergebnisse können unzuverlässig sein, wenn umfangreiches Versagen auftritt.
- Die Volumenänderung aufgrund von Änderungen in der Schubspannung (Schubdilatanz) wird nicht berücksichtigt.
- Eingabeparameter sind keine wesentlichen Bodeneigenschaften, sondern nur empirische Werte für einen begrenzten Bereich von Bedingungen.
- Das Modell ist hauptsächlich für quasi-statische Analysen gedacht.
Referenz:
- Duncan, J. M. and Chang, C. Y., Nonlinear analysis of stress and strain in soils, Journal of the Soil Mechanics and Foundations Division, ASCE, 96(SM5), 1629-1653, 1970.
- Kulhawy, F. H. and Duncan, J. M., Stresses and movements in Oroville Dam, Journal of the Soil Mechanics and Foundations Division, ASCE, 98(SM7), 653-655, 1972.
- 3. Duncan, J. M., Byrne, P., Wong, K. S. and Mabry, P., Strength, stress-strain and bulk modulus parameters for finite element analysis of stresses and movements in soil masses, Report No. UCB/GT/80-01, Dept. Civil Engineering, U.C. Berkeley, 1980.