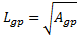Average Element Thickness
The 11th user material constant defines the average element thickness used with energy-based degradation. For two-dimensional elements this value is ignored. For three-dimensional (solid) elements this is the average thickness of solid elements associated with the material, where the thickness is defined as the interlaminar dimension of the element.
Recall from Appendix A.5 that the final effective strain used in the energy-based degradation calculations is given by

In the above, Le is the representative element length as defined by MSC Nastran. In the case of three-dimensional elements (i.e. bricks and continuum shell) the element length is the cubed root of the volume. In the case of two-dimensional elements (i.e. shell and plane stress elements) the element length is the square root of the area.
For two-dimensional elements, the element thickness is ignored. The representative element length provides a measure of the in-plane area of the element, which gives us a meaningful measure to associate with a composite ply. However, for layered solid elements the representative element length is not associated with a measure for a single ply. To accommodate the use of solid elements and allow them to be used and compared against results for two-dimensional elements, the representative element length must be modified to provide a useful measure of the element length in the plane of a ply.
Composite fractures almost always occur in the plane of the lamina. Therefore, it is more accurate to neglect the through thickness size of the element. This is done by using the average element thickness constant supplied in the user material definition. The representative element length is then calculated as follows:
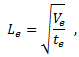
where Ve is the volume of the element, and te is the average thickness of the element. The element length defined in the equation above provides an accurate measure of the in-plane area of a solid element, and will collapse to the exact measure provided by MSC Nastran for two-dimensional elements when the thickness of a solid element is constant.
In Helius PFA for MSC Nastran, the representative element length must be calculated at the Gauss point level, because only the Gauss point volume, Vgp, is retrievable, not the element volume Ve. Therefore, the representative Gauss point length, Lgp, is calculated instead. In a similar fashion, the average thickness supplied with the user material constant should actually be given as the average Gauss point thickness, tgp. As a result, the representative element length is calculated with the equation below:
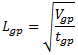
Using a length representative of the Gauss point size is more accurate than using a length representative of the element since the material constitutive behavior is applied at the Gauss point level. Determining the average Gauss point thickness is dependent on the size of the element, the chosen element type, integration scheme, and number of layers and layer thicknesses if layered element technology is used.
The equation above is only applicable to solid continuum elements. For shell elements, Helius PFA retrieves the area of the Gauss point, Agp, which neglects the thickness of the Gauss point. Therefore, the modified representative element Gauss point length is calculated by simply taking the square root of the Gauss point area: