About Spiral Definitions

Various transition curves are used in civil engineering to gradually introduce curvature and superelevation between both tangents and circular curves as well as between two circular curves with different curvature.

In its relationship to other tangents and curves, each spiral is either an incurve or an outcurve.

The two most commonly used parameters by engineers in designing and setting out a spiral are L (spiral length) and R (radius of circular curve).

The following illustration shows the various parameters of a spiral:

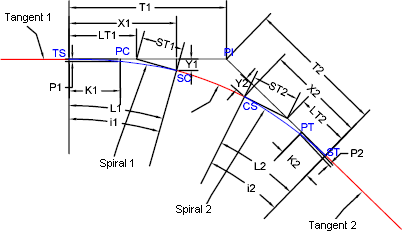
Spiral Parameter	Description
i1	The central angle of spiral curve L1, which is the spiral angle.
i2	The central angle of spiral curve L2, which is the spiral angle.
T1	The total tangent distance from PI to TS.
T2	The total tangent distance from PI to ST.
X1	The tangent distance at SC from TS.
X2	The tangent distance at CS from ST.
Y1	The tangent offset distance at SC from TS.
Y2	The tangent offset distance at CS from ST.
P1	The offset of the initial tangent into the PC of the shifted curve.
P2	The offset of the initial tangent out to the PT of the shifted curve.
K1	The abscissa of the shifted PC referred to the TS.
K2	The abscissa of the shifted PT referred to the ST.
LT1	The long tangent spiral in.
LT2	The long tangent spiral out.
ST1	The short tangent spiral in.
ST2	The short tangent spiral out.
	Other Spiral Parameters
A1	The A value equals the square root of the spiral length multiplied by the radius. A measure of the flatness of the spiral.
A2	The A value equals the square root of the spiral length multiplied by the radius. A measure of the flatness of the spiral.

Formula

Compound Spiral

Compound spirals provide a transition between two circular curves with different radii. As with the simple spiral, this allows for continuity of the curvature function and provides a way to introduce a smooth transition in superelevation.

Clothoid Spiral

While AutoCAD Civil 3D supports several spiral types, the clothoid spiral is the most commonly used spiral type. The clothoid spiral is used world wide in both highway and railway track design.

First investigated by the Swiss mathematician Leonard Euler, the curvature function of the clothoid is a linear function chosen such that the curvature is zero (0) as a function of length where the spiral meets the tangent. The curvature then increases linearly until it is equal to the adjacent curve at the point where the spiral and curve meet.

Such an alignment provides for continuity of the position function and its first derivative (local azimuth), just as a tangent and curve do at a Point of Curvature (PC). However, unlike the simple curve, it also maintains continuity of the second derivative (local curvature), which becomes increasingly important at higher speeds.

Formula

Clothoid spirals can be expressed as:

Flatness of spiral:

Total angle subtended by spiral:

Tangent distance at spiral-curve point from tangent-spiral point is:

Tangent offset distance at spiral-curve point from tangent-spiral point is:

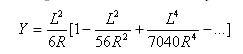
Bloss Spiral

Instead of using the clothoid, the Bloss spiral with the parabola of fifth degrees can be used as a transition. This spiral has an advantage over the clothoid in that the shift P is smaller and therefore there is a longer transition, with a larger spiral extension (K). This factor is important in rail design.

Formula

Bloss spirals can be expressed as:

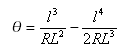
Other key expressions:

Tangent distance at spiral-curve point from tangent-spiral point is:

Tangent offset distance at spiral-curve point from tangent-spiral point is:

Sinusoidal Curves

These curves represent a consistent course of curvature and are applicable to transition from 0 through 90 degrees of tangent deflections. However, sinusoidal curves are not widely used because they are steeper than a true spiral and are therefore difficult to tabulate and stake out.

Formula

Sinusoidal curves can be expressed as:

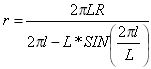
where r is the radius of curvature at any given point.

Sine Half-Wavelength Diminishing Tangent Curve

This form of equation is commonly used in Japan for railway design. This curve is useful in situations where you need an efficient transition in the change of curvature for low deflection angles (in regard to vehicle dynamics.)

Formula

Sine Half-Wavelength Diminishing Tangent curves can be expressed as:

where and x is the distance from the start to any point on the curve and is measured along the (extended) initial tangent; X is the total X at the end of the transition curve.

Other key expressions:

Tangent distance at spiral-curve point from tangent-spiral point is:

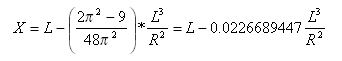
Tangent offset distance at spiral-curve point from tangent-spiral point is:

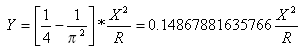
Cubic Parabolas

Cubic parabolas converge less rapidly than cubic spirals, which makes their use popular in railway and highway design.

Formula

Minimum Radius of Cubic Parabola

The radius at any point on a cubic parabola is:

A cubic parabola attains minimum r at:

A cubic parabola radius decreases from infinity to at 24 degrees, 5 minutes, 41 seconds and from then onwards starts to increase again. This makes cubic parabolas useless for deflections greater than 24 degrees.

Cubic (JP)

This transition was developed for requirements in Japan. Some approximations of the clothoid have been developed to use in situations to accommodate a small deflection angle or a large radius. One of these approximations, used for design in Japan, is Cubic (JP).

Formula

Cubic (JP) can be expressed as:

Where X = Tangent distance at spiral-curve point from tangent-spiral point

This formula can also be expressed as:

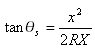
Where is central angle the spiral (illustrated as i1 and i2in the illustration)

Other key expressions:

Tangent distance at spiral-curve point from tangent-spiral point is:

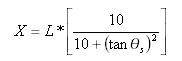
Tangent offset distance at spiral-curve point from tangent-spiral point is:

Bi-Quadratic (Schramm) Spirals

Bi-quadratic (Schramm) spirals have low values of vertical acceleration. They contain two second-degree parabolas whose radii vary as a function of curve length.

Simple Curve Formula

Curvature of the first parabola:

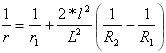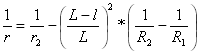for