This section provides a list of validation problems for Shape Generator. Whenever possible, it is important to compare Shape Generator with known or theoretical solutions to understand where it can be used reliably.
Tensile Cube
In this problem, the top of a cube is loaded in tension. The four corners on the bottom surface of the cube are constrained in the direction of the load, but are free to slide in the plane.
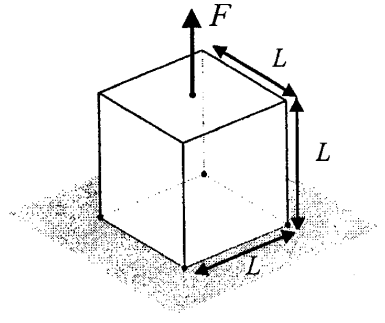

Using Shape Generator, we are able to reproduce the expected result. Notice that with the sliding boundary conditions, the horizontal bars on the bottom of the cube are present, which is consistent with published results [1].

Now we modify the boundary conditions so that all displacements are fixed at the four corners on the bottom surface of the cube (the homogenous Dirichlet condition). We expect to see a shape with only the four diagonal members [1].

Cantilever Beam
In this problem, a cantilever beam (L = 40, H = 25, W = 1) is loaded by a point load acting on the free end of the beam. The point load is applied midway up the free end of the beam. The beam is made from an isotropic material with a Young's modulus of 106 and a Poisson ratio of 0.25.
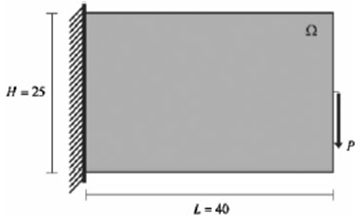
The published results below show the optimal beam geometry with 50% of the original design domain volume for varying minimum allowable member diameters [2].

Using Shape Generator, we are able to reproduce a very similar result to case (b) in which the minimum member diameter = 2. Shape Generator does not currently impose a minimum member size. To produce a part with thin members, you should use a higher resolution mesh as demonstrated below.
One noticeable difference with the Shape Generator result is the material remaining at the fixed (left) end of the beam. Since a boundary condition was applied at this location, the material along this face was automatically preserved. Faces with applied loads and constraints will automatically be maintained when running Shape Generator.

Bridge
In this problem, we aim to determine the support structure required to support a uniformly distributed load acting on an area. As shown in the picture below, there are three fixed constraints on the bottom of the structure [1].
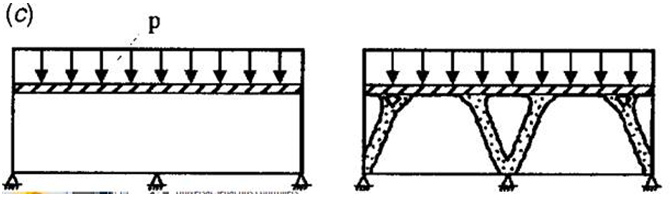
Using Shape Generator, we model this structure as a beam with a uniformly distributed load applied to the top. The three fixed constraints are applied to the bottom of the beam, with one at each end and one at mid-length. The result below agrees well with the published solution. The generated shape takes the form of a bridge deck built on two supporting arches which are able to transmit the compressive pressure load to the fixed constraints.

Hemispherical Shell
In this problem, a thin, hemispherical shell is examined. The shell has a hole opening at the top, around which a pressure load is applied. The y-displacements are fixed on the bottom edge of the hemisphere. The x and z-displacements are fixed around the hole opening on the top of the hemisphere [3].
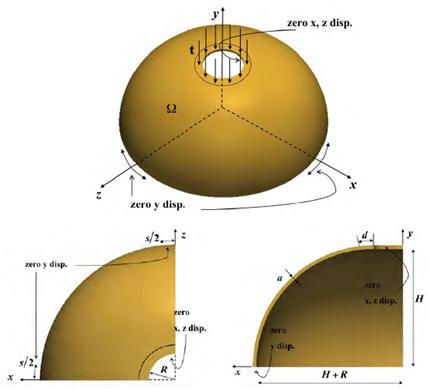
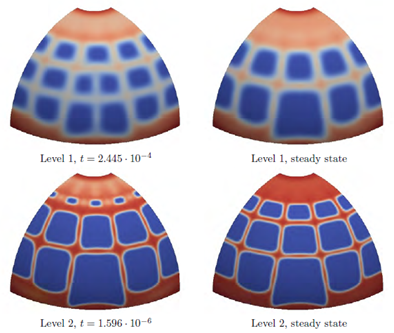

Using Shape Generator, we are able to reproduce the published result. While much of the generated result agrees with the published results, some noticeable differences occur on the bottom edge of the hemisphere. In the Shape Generator result, only a thin layer of material is remaining where the boundary conditions are applied. The published results show a much thicker band of material around the bottom edge of the hemisphere. The published results also show some variance in thickness of this band of material, likely due to the symmetry boundary conditions used.

References
- Eschenauer, H.A., and Olhoff, N. (2001) "Topology Optimization of Continuum Structures," Journal of Applied Mechanics Reviews. 54(4): 372.
- Guest, J.K., Prevost, J.H., and Belytschko, T. (2004) "Achieving Minimum Length Scale in Topology Optimization Using Nodal Design Variables and Projection Functions," International Journal for Numerical Methods in Engineering. 61(2): 238-254.
- Dede, L., Borden, M.J., and Hughes, T.J.R. (2012) "Isogeometric Analysis for Topology Optimization with a Phase Field Model," Archives of Computational Methods in Engineering. 19(3): 427-465.