Returns the cosine of an angle specified in radians.
float cos(float number)
number is the angle, in radians, whose cosine you want.
For any right triangle, the cosine of an angle is the following ratio:
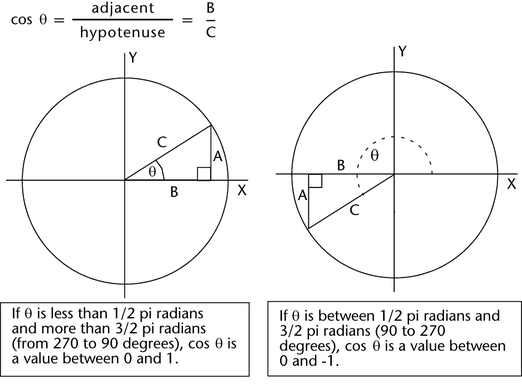
The cosine ratio depends only on the size of the angle and not on the size of the triangle. This constant ratio is called the cosine of the measure of the angle.
The cosine ratio is a value between -1 and 1.
With a steadily increasing or decreasing argument, the cos function returns steadily increasing or decreasing values between 1 and -1. This is useful for creating rhythmic, oscillating changes in attribute values.
The cos function works like the sin function except its return values are 90 degrees, or pi/2, out of phase.
See sin for ideas on how to use the cyclical characteristics of the sin and cos functions.
Example 1
cos(1)
Returns 0.5403, the cosine of 1 radian.
Example 2
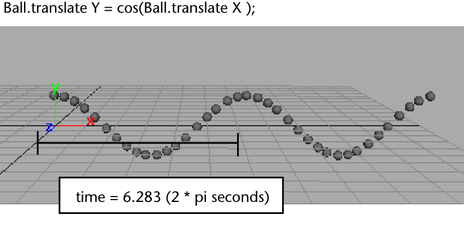
To animate the motion of Ball in a cosine wave pattern, use this expression:
Ball.translateX = time; Ball.translateY = cos(Ball.translateX);
Ball starts at the origin and moves in the X direction at a rate set by the incrementing animation time. Its Y translation moves cyclically up and down according to the return values of the cos function. The cos function uses translateX, and therefore indirectly, time, as its argument.
As time increases from 0 to 6.283 seconds, the cos function returns values that change in fine increments from 1 to -1 and back to 1. The value 6.283 is 2 times the value of pi.
As time increases beyond 6.283 seconds, the same cycle repeats for each span of 6.283 seconds.
Compare the same expression using the sin function:
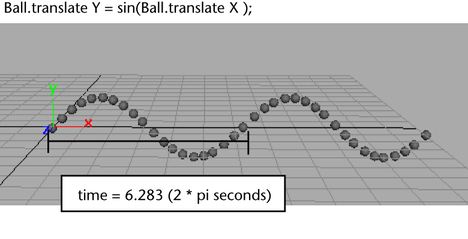
The cosine curve is 1.571 (pi/2) seconds ahead of (or behind) the sine curve, and vice versa.