Returns values along a hermite curve. You can use the hermite function, for instance, to move an object smoothly along a curve. As the following examples show, you can create various curve shapes by altering the arguments to the hermite function.
vector hermite(vector start, vector end, vector tan1, vector tan2, float parameter)
float hermite(float start, float end, float tan1, float tan2, float parameter)
start is the start point of the curve.
end is the end point of the curve.
tan1 is the tangent vector that guides the direction and shape of the curve as it leaves the start point of the curve. The vector’s position starts at the start point of the curve.
tan2 is the tangent vector that guides the direction and shape of the curve as it approaches the end point of the curve. The vector’s position starts at the end point of the curve.
parameter is an floating point value between 0 and 1, for example, the value returned by a linstep function.
In the second format, the arguments and return values work in a single dimension.
Example 1
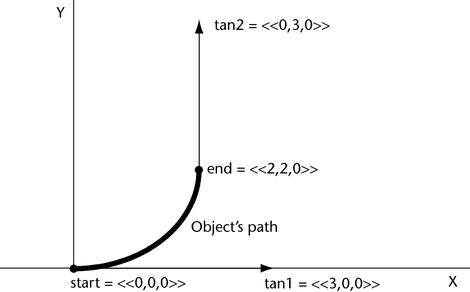
Suppose you create an object named dust made of one sphere at the origin. To guide its motion along a short upward-bound curve for the first four seconds of animation, you can write the following runtime expression:
dust.position = hermite(<<0,0,0>>,<<2,2,0>>, <<3,0,0>>, <<0,3,0>>, linstep(0,4,time));
When you play the animation, the object moves from the start point <0,0,0> along a curve to the end point <2,2,0>. The tangent vector <3,0,0> sets the curve’s direction and shape as it leaves the start point. The tangent vector <0,3,0> sets the curve’s direction and shape as it approaches the end point.
From zero to four seconds of animation play, the object moves along the curve as defined by the linstep function. (See linstep for details.)
The function arguments and resulting path of the object follow:
Example 2
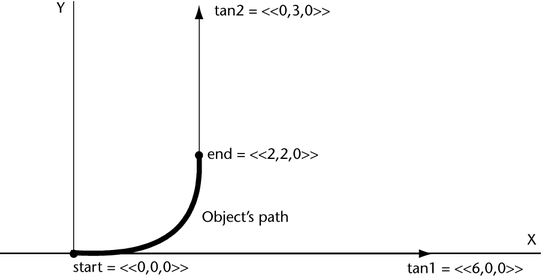
Suppose you change the third argument of the previous example expression to <<6,0,0>>:
dust.position = hermite(<<0,0,0>>,<<2,2,0>>, <<6,0,0>>, <<0,3,0>>, linstep(0,4,time));
The slope of the path curve steepens because of the longer tan1 vector:
Example 3
The following expression moves dust in an S pattern:
dust.position = hermite(<<0,0,0>>,<<2,0,0>>, <<0,3,0>>, <<0,3,0>>, linstep(0,4,time));
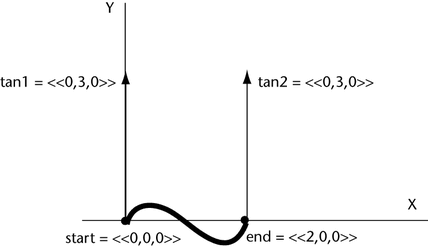
The tan1 vector <<0,3,0>> sets the direction of the curve from the start point to a positive Y direction. The tan2 vector <<0,3,0>> sets the direction of the curve to a positive Y direction as it approaches the end point.
Values between the start and end point curves are interpolated to form an S pattern.
Example 4
Suppose you change the fourth argument of the previous example expression to <<0,-3,0>>:
dust.position = hermite(<<0,0,0>>,<<2,0,0>>, <<0,3,0>>, <<0,-3,0>>, linstep(0,4,time));
The dust object moves in a pattern resembling a half-circle:
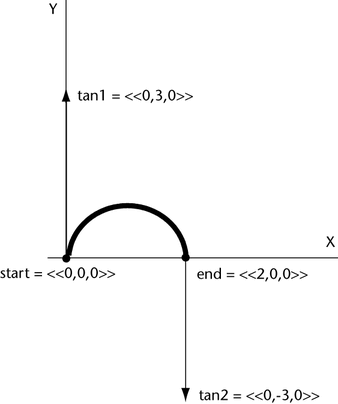
The tan1 vector <<0,3,0>> sets the direction of the curve from the start point to a positive Y direction. The tan2 vector <<0,-3,0>> sets the direction of the curve to a negative Y direction as it approaches the end point.
Example 5
Suppose you change the third argument of the preceding example to <<0,10,0>>:
dust.position = hermite(<<0,0,0>>,<<2,0,0>>, <<0,10,0>>, <<0,-3,0>>, linstep(0,4,time));

Because of the longer tan1 vector, the slope of the path curve steepens as it rises from the start point. Because the tan2 vector has a smaller Y magnitude than the Y magnitude of the tan1 vector, the slope of the path curve is flatter as it approaches the end point. The curve’s rise in the Y direction is greater than the previous example because the magnitude of tan1’s Y component is larger (10 instead of 3).