The 3D flow results are based on the following considerations.
To simulate the flow inside the mold cavity, the conservation equations of momentum, mass and energy are discretized into finite elements.
This is defined by the following equations:
Conservation of mass for a fluid
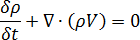
Where
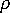is the polymer density 
is time 
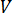is the velocity vector
Conservation of momentum
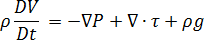
Where
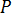is pressure 
is the viscous stress tensor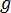 
is the gravitational acceleration vector
Conservation of energy
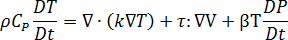
Where
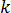is the polymer thermal conductivity 
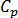is the specific heat capacity of the melt 
is the polymer expansivity which is defined as follows
For the pressure-velocity (momentum and mass conservation) solution.
- The equations are solved by a standard finite element method. This includes the material compressibility in all process stages.
- The beam and tetrahedral elements are solved simultaneously.
- All the tetrahedral nodes in the shadow of each beam element are tied to the same pressure.
- In beam elements, a 1D flow is assumed and a Hele-Shaw approximation is used.
- In tetrahedral elements, a full Stokes solution is performed (or Navier-Stokes if the inertia option is selected) .
For the temperature (energy conservation) solution
- Equations are solved by a standard finite element method.
- For both beam and tetrahedral elements, we include the shear heating, convection, conduction and compressive heating terms.
- In the beam elements, we approximate negligible conduction along the beam length. For temperature convection in beam elements, we upwind within each beam laminate.
- When solving the temperature equations, we break the time-step into a number of shorter sub-steps for increased accuracy.
At each time-step, we iterate between the temperature and pressure-velocity equations until convergence is reached.