Centrifugal Load

Note: The information in this section applies to all linear and nonlinear analyses that support centrifugal loads.

A centrifugal load simulates the effect of the entire model spinning about an axis you specify. Only parts with a nonzero material mass density are affected. The model does not actually experience rotation. Rather, the equivalent forces that would occur as a result of angular rotation and/or angular acceleration are calculated and applied to the nodes of each element.

Linear Analyses

Three types of linear analysis support centrifugal loads—Static Stress with Linear Material Models, Natural Frequency (Modal) with Load Stiffening, and Critical Buckling. The model can be spinning at a constant rate and/or can be undergoing a constant angular acceleration rate.

The command implementation is slightly different among the linear analyses. In all three cases, the actual load is defined within the Centrifugal tab of the Analysis Parameters dialog box, and the axes of rotation and angular acceleration can pass through any point is 3D space (that is, the axes do not have to pass through the global coordinate origin). The differences are as follows:

Nonlinear Analyses

Two types of nonlinear analysis support centrifugal loads—MES and Static Stress with Nonlinear Material Models. Load curves control both the rotation speed and the angular acceleration rate over time. The same load curve can be used for both, or you can specify two different load curves for rotation and angular acceleration. The centrifugal load is defined within the Centrifugal tab of the Advanced Analysis Parameters dialog box and can be accessed using one of the following two methods:

  1. Use the ribbon command, Setup Loads Centrifugal.
  2. Access the Analysis Parameters dialog box (either via the browser or ribbon), click the Advanced button, and click on the Centrifugal tab.

For either type of nonlinear analysis that supports centrifugal loads...

Apply Centrifugal Loads

To apply a centrifugal load to a model...

  1. Access the appropriate dialog box using one of the methods described above (differs among the various analysis types).
  2. If included within the dialog box, activate the Include specified centrifugal load checkbox.
  3. Specify the appropriate magnitudes under Angular Velocity (Omega) and Angular Acceleration (Alpha).
  4. For nonlinear analyses, select the load curve numbers to use for angular velocity and angular acceleration.
  5. Specify the axis orientation using one of the methods described above (differs among the various analysis types). For some analysis types, the rotation and angular acceleration axes may be different, and for others, the same axis must be used for both (as detailed above). In addition, some analysis types support non-global axis orientations and others do not (also as detailed above). Use the Point on Axis coordinates and the Direction coordinates or pull-down global axis list to specify the location and direction of the axis (or axes) . The angular rotation follows the right-hand rule about the vector you define.
  6. For linear static stress analyses, set the Omega and/or Alpha global load case multipliers within the Multipliers tab of the Analysis Parameters dialog box.
    Tip: A nonzero multiplier is required to activate the load. See the page Analysis Parameters: Static Stress with Linear Material Models.

For example, take the circle centered at the origin in Figure 1. To specify rotation about the Z axis at the origin, enter Point on Axis coordinates of (0,0,0) and Direction coordinates of (0,0,1) - the circle rotates about its center and the center of the circle remains stationary.

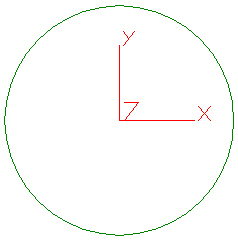
Figure 1: Model 1 Rotating About Origin

However, if you have the circle as shown in Figure 2 centered at (3,0,0) with the same settings for the centrifugal load, the load is based on rotation of the circle about the origin. In other words, the center of the circle moves in a circular path about the global origin. Figure 3 shows a graphical depiction of the path of the circle from Figure 2 under the specified centrifugal load.

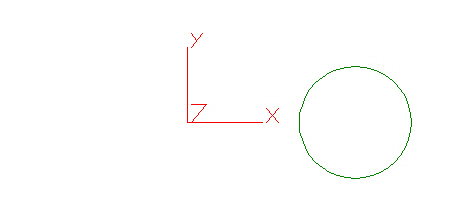
Figure 2: Model 2 – Circle with its Center Not at the Global Origin

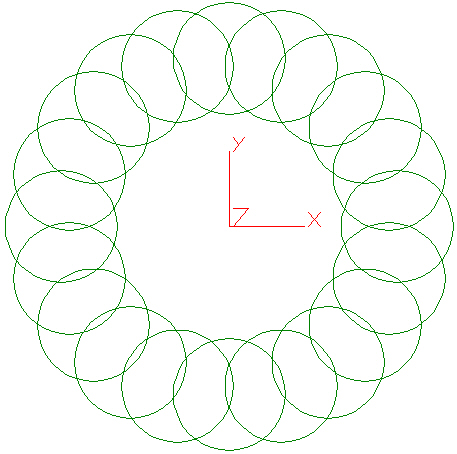
Figure 3: Interpretation of Model 2 Rotating About Origin

Note: For all three linear analyses that support centrifugal loads, remember that, despite the simulated motion effects, these are still static analyses. Therefore, the model needs to be statically stable in all directions. Typically, a rotating part or assembly is attached to a shaft or lever. Two common constraint schemes are as described below:
  • Fully-fix the area or areas of attachment to the supporting shaft or lever.
  • Alternatively, constrain tangential motion along the surface of the hole where the rotating parts are fit to the shaft or lever. This constraint takes care of two of the three translational degrees of freedom. In addition, constrain a point, edge, or surface against translation in the axial direction. For example, constrain the area of contact with the shaft shoulder against translation in the normal direction, which prevents axial motion under thrust loads and takes care of the third translational DOF.

Parent topic: Loads and Constraints