Los fenómenos electromagnéticos de la calefacción de inducción se describen matemáticamente mediante ecuaciones de Maxwell.
Las ecuaciones de Maxwell en formato diferencial se pueden escribir de la siguiente manera:
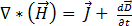(según la ley de Ampère) [1]
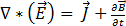(según la ley de Faraday) [2]
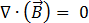(según la ley de Gauss) [3]
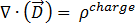(según la ley de Gauss) [4]
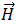es la intensidad del campo magnético, 
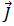es la densidad de corriente de conducción, 
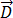es la densidad del flujo eléctrico, 
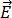es el campo eléctrico, 
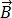es la densidad del flujo magnético, 
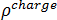es la densidad de la carga eléctrica y 
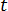es el tiempo.
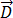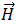y pueden estar relacionados con 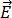y 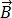mediante las propiedades de material electromagnético de permitividad, 
, y permeabilidad magnética,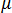 
, de acuerdo con las siguientes ecuaciones:
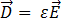[5]
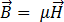[6]
Las ecuaciones de Maxwell se pueden reducir más con la ley de Ohm:
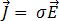[7]
Al sustituir las ecuaciones [5] y [7] en la ecuación [1] y teniendo en cuenta que para las frecuencias de corriente menores de 10 MHz la corriente inducida, 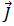, es mayor que la densidad de corriente desplazada, 
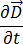, se da por hecho que este término se puede omitir y que la ecuación [1] se puede escribir como:
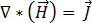[8]
Como la densidad de flujo magnético, 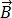, cumple la divergencia cero de la ecuación [3], puede expresarse como potencial de vector magnético, 
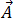, de forma que:
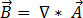[9]
La sustitución de la ecuación [9] en la ecuación [2] da:
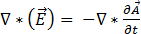[10]
Por lo tanto,
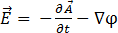[11]
donde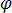 
es el potencial eléctrico escalar. La ecuación [7] ahora se convierte en:
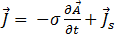[12]
donde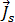 
es la amplitud de la densidad de corriente de origen en la bobina y viene dada por:
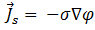[13]
Al sustituir las ecuaciones [6], [9] y [12] en la ecuación [8] obtenemos:
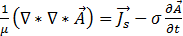[14]
Ahora, usando la ecuación de identidad de vectores de productos triples 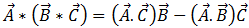[15]
[15]
en la ecuación [14], obtenemos:
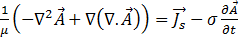[16]
Ahora, teniendo en cuenta que para un campo de potencial vectorial del componente
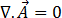[17]
la ecuación [16] se reduce a
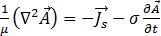[18]
Para el estado constante sinusoidal con frecuencia angular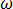 
= 2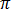
F y unidades (rad/s), la ecuación [18] se convierte en:
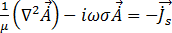[19]
Una vez que se resuelve el potencial vectorial magnético armónico temporal,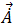 
, la densidad de flujo del campo magnético puede encontrarse en la ecuación [9]. La corriente turbulenta inducida armónica temporal, 
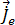, en los conductores viene determinada por la ecuación 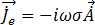[20]:
[20]
A partir de la cual se encuentra el calor en Julios,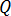 
, de los conductores:
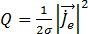[21]
El calor en Julios es el origen de calor volumétrico, con unidades (W/m3), que es inducido por la corrientes turbulentas del conductor.
El fenómeno de transferencia de calor que se produce en la calefacción de inducción es la conducción del calor dentro del conductor y se describe con la ecuación de conducción de calor transitoria que se usa en todas las simulaciones.
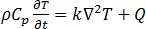[22]
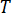es el temperatura, 
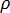es la densidad, 
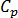es la capacidad de calor específica, 
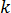es la conductividad térmica del material y 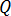- es el calor en Julios de la ecuación [21].