Fillet Arc
Ajoutez un raccord à l'intersection de deux liens.
Propriétés
Spécifiez les paramètres suivants dans le groupe de fonctions Properties.
| Lien | |
| Link Number | Spécifie le numéro du lien. Vous pouvez modifier le numéro du lien généré automatiquement. |
| Link Codes | Spécifie les codes affectés au lien. |
| Propriétés de géométrie | |
| First Link | Spécifie le lien entrant au niveau du raccord. |
| Second Link | Spécifie le lien sortant au niveau du raccord. |
| Tessellation | Indique le nombre de segments de ligne utilisés pour représenter la courbe. Remarque : Cette valeur doit être comprise entre 2 et 100.
Cliquez sur [...] pour ouvrir l'éditeur d'expressions, dans lequel vous pouvez saisir ou calculer une valeur. |
| Round By | Spécifie le paramètre selon lequel définir le raccord :
|
| Round Parameter | Valeur à appliquer au paramètre Round By. |
| Points | |
| Start Point Name | Spécifie le nom du point de départ. Vous pouvez modifier le numéro du point généré automatiquement. |
| Start Point Code | Spécifie les codes affectés au point de départ. |
| End Point Name | Spécifie le nom du point d'arrivée. Vous pouvez modifier le numéro du point généré automatiquement. |
| End Point Code | Spécifie les codes affectés au point d'arrivée. |
| Divers | |
| Comment | Indique des remarques concernant le lien. Des commentaires peuvent être affichés dans le groupe de fonctions Preview. |
Exemple
Pour consulter un exemple d'utilisation de cet élément de géométrie, ouvrez le fichier d'exemple PKT suivant :
Fillet Arc Example.pkt
L'exemple PKT contient un exemple de lien d'arc à un raccord. Pour consulter les paramètres, sélectionnez le lien Fillet Arc dans l'organigramme, puis examinez le groupe de fonctions Properties.
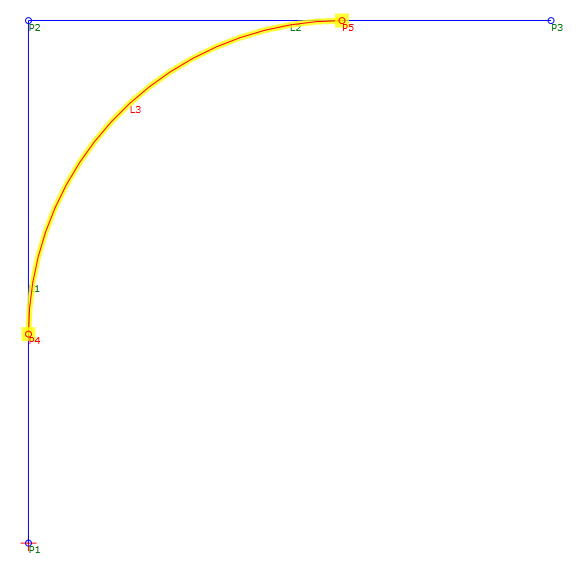
Dans l'exemple, L3 forme un raccord entre L1 et L2 L3 est défini par un rayon de valeur 3 et possède une valeur de maillage par approximation de 20. Si l'un des liens est modifié, L3 conserve ses paramètres de définition, ainsi que sa tangence à L1 et L2.
