Vous pouvez vous procurer les équations de base pour les chaînes linéaires fermées de cotes dans l'image ci-dessous.
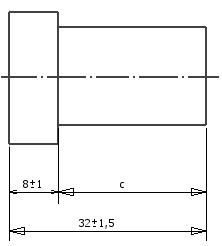
a = 32 ± 1.5 mm, b = 8 ± 1 mm
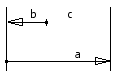
Eléments d'augmentation/réduction
Si l'élément d'augmentation s'accroît, l'élément de fermeture augmente également. Si l'élément de réduction augmente, l'élément de fermeture diminue si d'autres éléments de la chaîne restent constants.
|
Elément de fermeture : |
1. c = a - b |
|
Cote maximale de l'élément de fermeture : |
2. c max = a max - b min |
|
Cote minimale de l'élément de fermeture : |
3. c min = a min - b max |
|
Tolérance de l'élément de fermeture (par soustraction de l'équation 3 à l'équation 2) : |
4. c max - c min = a max - a min - (b min - b max ) |
|
Tel que |
5. T c = T a + T b |
Généralement, les tolérances des chaînes linéaires satisfont l'équation suivante.
![]()
De même, les équations 2 et 3 peuvent être écrites sous une forme générale.
![]()
![]()
La cote maximale de l'élément de fermeture équivaut à une différence entre la somme des cotes maximales des éléments d'augmentation et la somme des cotes minimales des éléments de réduction.
La cote maximale de l'élément de fermeture équivaut à une différence entre la somme des cotes maximales des éléments d'augmentation et la somme des cotes minimales des éléments de réduction.
La cote nominale de l'élément de fermeture peut être exprimée à l'aide de l'équation 1, comme dans l'équation suivante.
![]()
Déviation maximale de l'élément de fermeture.
![]()
Déviation minimale de l'élément de fermeture.
![]()