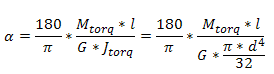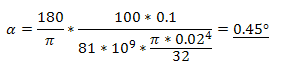Ces formules permettent de résoudre un arbre (à une ou plusieurs coupes) ou une poutre (à une coupe constante) avec plusieurs supports et plusieurs charges.
L'axe de l'arbre ou de la poutre est aligné par rapport à l'axe Z. Si l'impact de la densité de la matière est pris en compte dans le calcul, le vecteur de gravité est aligné par rapport à l'axe Y.
Forces de cisaillement :
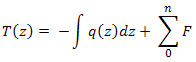
Moments de flexion :
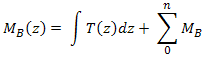
Angle de flexion :
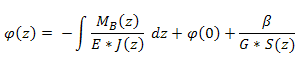
où :
|
E |
module d'élasticité en tension |
|
|
J |
moment d'inertie |
|
|
G |
module de rigidité |
|
| β |
coefficient de déformation de cisaillement |
Flexion :
![]()
Contrainte de pliage :
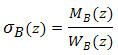
Contrainte de cisaillement :
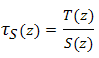
Contrainte de torsion :

Contrainte de tension :
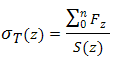
Contrainte réduite :
![]()
où :
| σ B | contrainte de pliage | |
| σ T |
contrainte de tension |
|
| τ | contrainte de torsion | |
| τ S | contrainte de cisaillement | |
| α | α = 3 pour HMH | |
| α = 4 pour Tresca-Invité |
Exemple de calcul
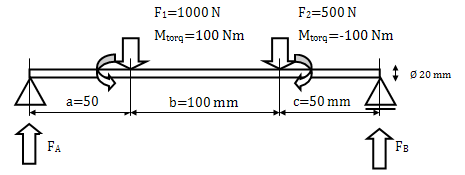
Module d'élasticité E = 210 000 MPa
Module de rigidité G = 81 000 MPa
Coefficient de déformation de cisaillement β = 1.118
Mode de calcul avec contrainte réduite : HMH
N'incluez pas la densité de la matière.
Forces de support :
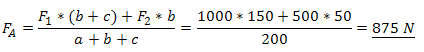

Contrainte de cisaillement maximale :
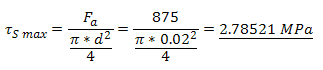
Contrainte de torsion maximale :
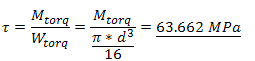
Moment maximal :
![]()
Contrainte de pliage maximale :
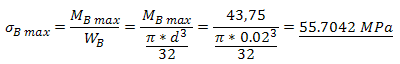
Contrainte réduite maximale :

Angle de torsion :