Courbes de fatigue dans les liaisons fixes

Différents types de courbes de fatigue peuvent être utilisés pour déterminer la résistance à la fatigue des liaisons fixes. Vous trouverez ci-dessous des formules pour établir les courbes individuelles des contraintes normale et de cisaillement.

1. Méthode de calcul de la tension de Reynolds moyenne

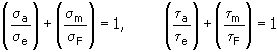
où :

	σ a , τ a	amplitude d'une contrainte (de cisaillement) normale [MPa, psi]
	σ e , τ e	limite d'endurance à force constante [MPa, psi]
	σ m , τ m	sollicitation périodique moyenne [MPa, psi]
	σ F , τ F	tension de Reynolds moyenne [MPa, psi]
	Ψ	facteur de réduction du diagramme de Haigh [-]
		Dépend de la matière de la liaison (valeurs recommandées) pour traction et flexion Ψ<0.15...0.3>
		- pour cisaillement Ψ <0.1...0.25>.

2. Méthode Godman modifiée

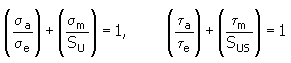
où :

	σ a , τ a	amplitude d'une contrainte (de cisaillement) normale [MPa, psi]
	σ e , τ e	limite d'endurance à force constante [MPa, psi]
	σ m , τ m	sollicitation périodique moyenne [MPa, psi]
	S U	résistance ultime à la traction [MPa, psi]
	S US	résistance ultime au cisaillement [MPa, psi]
		où S US ≈ 0.8 S U

3. Méthode quadratique (elliptique)

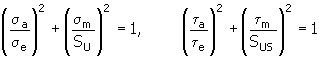
Pour une explication des variables, reportez-vous à la méthode Godman modifiée.

4. Méthode parabolique de Gerber

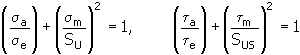
Pour une explication des variables, reportez-vous à la méthode Godman modifiée.

5. Méthode de Keccecioglu, Chester et Dodge

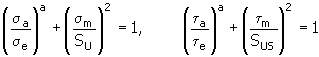
où :

	σ a , τ a	amplitude d'une contrainte (de cisaillement) normale [MPa, psi]
	σ e , τ e	limite d'endurance à force constante [MPa, psi]
	σ m , τ m	sollicitation périodique moyenne [MPa, psi]
	S U	résistance ultime à la traction [MPa, psi]
	S US	résistance ultime au cisaillement [MPa, psi]
		où S US ≈ 0.8 S U
	a	exposant en fonction de la matière de la liaison [-]
		valeurs recommandées a <2.6...2.75>

6. Méthode de Bagci

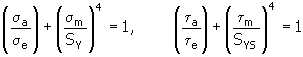
où :

	σ a , τ a	amplitude d'une contrainte (de cisaillement) normale [MPa, psi]
	σ e , τ e	limite d'endurance à force constante [MPa, psi]
	σ m , τ m	sollicitation périodique moyenne [MPa, psi]
	S Y	limite d'élasticité en traction [MPa, psi]
	S YS	limite d'élasticité en cisaillement [MPa, psi]
		où S YS ≈ 0.577 S Y

7. Méthode Soderberg

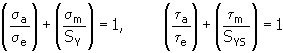
Pour une explication des variables, reportez-vous à la méthode de Bagci.