Les phénomènes électromagnétiques de chauffage par induction sont décrits mathématiquement par des équations de Maxwell.
Les équations de Maxwell, dont la structure varie, peuvent s'écrire comme suit :
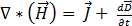(théorème d'Ampère) [1]
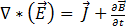(loi de Faraday) [2]
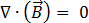(loi de Gauss) [3]
(loi de Gauss) [4]
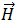désigne l'intensité du champ magnétique, 
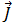désigne la densité du courant de conduction, 
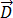désigne la densité du flux électrique, 
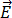désigne le champ électrique, 
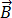désigne la densité du flux magnétique, 
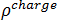désigne la densité de la charge électrique, et 
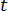désigne la durée.
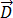et 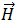peuvent être associés à 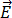et 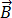par le biais des propriétés de matériaux électromagnétiques de permittivité (
) et de perméabilité magnétique (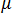
) selon les équations suivantes :
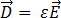[5]
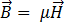[6]
La loi d'Ohm permet de simplifier les équations de Maxwell :
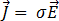[7]
Remplacez les équations [5] et [7] par l'équation [1], et notez que pour les fréquences de courant inférieures à 10 MHz, le courant induit (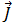) est supérieur à la densité de courant de déplacement (
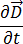). Ce terme peut donc être ignoré et l'équation [1] peut s'écrire comme suit :
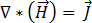[8]
Etant donné que la densité du flux magnétique (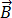) ne présente aucune divergence par rapport à l'équation [3], elle peut être exprimée sous la forme d'un potentiel vecteur magnétique (
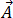) tel que :
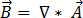[9]
Le remplacement de l'équation [9] par l'équation [2] permet d'obtenir le résultat suivant :
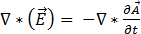[10]
Par conséquent,
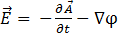[11]
où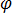 
désigne le potentiel scalaire électrique. L'équation [7] se présente alors comme suit :
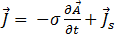[12]
où 
désigne l'amplitude de la densité du courant source dans la bobine, selon la formule suivante :
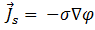[13]
Remplacer les équations [6], [9] et [12] par l'équation [8] permet d'obtenir le résultat suivant :
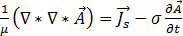[14]
A présent, le recours à l'équation d'identité vectorielle du produit triple 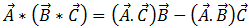[15]
[15]
dans l'équation [14] offre le résultat suivant :
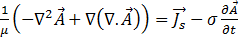[16]
Désormais, notez que pour un champ de potentiel vecteur de composant
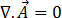[17]
l'équation [16] se réduit à
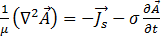[18]
Pour l'état stationnaire sinusoïdal avec une fréquence angulaire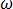 
de 2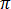
f et des unités (rad/s), l'équation [18] devient :
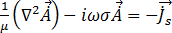[19]
Une fois le potentiel vecteur magnétique harmonique (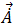
) résolu, la densité de flux du champ magnétique peut être dérivée de l'équation [9]. Les courants de Foucault harmoniques induits (
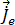) circulant dans les conducteurs sont fournis par l'équation 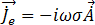[20] :
[20]
La chaleur (par effet Joule) (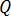
) des conducteurs peut être déduite de cette équation :
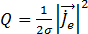[21]
La chaleur (par effet Joule) désigne la source de chaleur volumétrique, exprimée en W/m3, induite par les courants de Foucault dans le conducteur.
Le transfert de chaleur qui se produit lors du chauffage par induction correspond à la conduction thermique dans le conducteur. Ce phénomène est décrit à l'aide de l'équation de conduction thermique transitoire utilisée dans toutes les simulations.
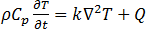[22]
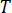désigne la température, 
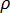désigne la densité, 
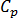désigne la capacité thermique spécifique, 
désigne la conductivité thermique de la matière, et 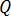- désigne la chaleur (par effet Joule) dérivée de l'équation [21].