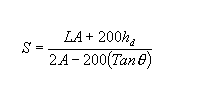Az AutoCAD Civil 3D képes értékeket számítani a magassági lekerekítések, MSP-információk, valamint objektum- és nézőpontmagasságok geometriai definíciójából.
Az értékek tapasztalati egyenletekből származnak, és nem használnak tervezési sebességet.
Domború lekerekítés esetén a program előzési és megállási látótávolságot használ, mert az ív csúcspontja akadályozhatja a vezető rálátását az út felületére vagy más objektumokra.
Homorú lekerekítés esetén a program nem használ előzési és megállási látótávolságot, mert nincs olyan ívcsúcspont, amely akadályozná a vezető rálátását az út felületére vagy más objektumokra. Homorú lekerekítés esetén nappal, jó látási viszonyok mellett a vezető teljes rálátással rendelkezik az útra. Éjjel azonban a vezető csak a fényszóró sugara által megvilágított távolságig lát. Homorú lekerekítés tervezéséhez használhatja a fényszóró látótávolságát.
Ezeket a tulajdonságokat az AutoCAD Civil 3D 2016 programban a Szövegkomponens-szerkesztővel jelenítheti meg. Az Eszköztár Beállítások lapján bontsa ki a Hossz-szelvény 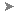 Feliratstílusok
Feliratstílusok  Ív elemet. Kattintson duplán az alapértelmezett domború és homorú feliratstílus elemre. Kattintson az Elrendezés lapra. A Komponens neve részen válasszon ki egy elemet, például a BVC elemet. A Szövegkomponens szerkesztőben kattintson a Tulajdonságok lehetőség alatt található legördülő nyílra az elérhető tulajdonságok megjelenítéséhez. Görgessen lefelé a tulajdonságok, például a Fényszóró látótávolsága, Előzési látótávolság stb. megtekintéséhez.
Ív elemet. Kattintson duplán az alapértelmezett domború és homorú feliratstílus elemre. Kattintson az Elrendezés lapra. A Komponens neve részen válasszon ki egy elemet, például a BVC elemet. A Szövegkomponens szerkesztőben kattintson a Tulajdonságok lehetőség alatt található legördülő nyílra az elérhető tulajdonságok megjelenítéséhez. Görgessen lefelé a tulajdonságok, például a Fényszóró látótávolsága, Előzési látótávolság stb. megtekintéséhez.
Domború lekerekítések létrehozása előzési és megállási látótávolságok alapján
Az előzési látótávolság az a távolság, amely ahhoz szükséges, hogy a vezető észlelhessen egy szembejövő járművet, és meghatározhassa, hogy van-e elegendő hely az előzésre. Az előzési látótávolság ritkán használatos a domború lekerekítések tervezésekor, mert az előzési látótér kritériumoknak való megfeleléshez szükséges ívhossz általában tiltó jellegű.
A megállási látótávolság, az ívhossz meghatározásához gyakran használt kritérium, az a távolság, amely a vezető számára az úton található veszély észleléséhez szükséges. Az előzési és megállási látótávolság követelményeit a kormányzati irányelvek határozzák meg.
A következő egyenletek az előzési és megállási látótávolság használatával számítják ki a domború lekerekítések hosszát:
ahol:
L = a magassági lekerekítés hossza lábban (vagy méterben)
S = a látótávolság lábban (vagy méterben)
A = algebrai különbség esésszázalékban (%)
h1 = a szemlélő szemmagassága az út felülete felett lábban (vagy méterben)
h2 = az objektum magassága az út felülete felett lábban (vagy méterben)
A következő egyenlet akkor igaz L-re, ha S kisebb, mint L:
A következő egyenlet akkor igaz S-re, ha S kisebb, mint L:
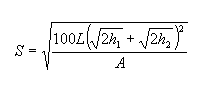
A következő egyenlet akkor igaz L-re, ha S nagyobb vagy egyenlő L-lel:
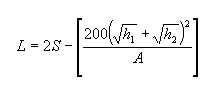
A következő egyenlet akkor igaz S-re, ha S nagyobb vagy egyenlő L-lel:
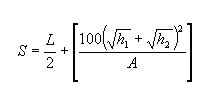
Homorú lekerekítések létrehozása a fényszóró látótávolsága alapján
Éjjel a jármű fényszórójának sugara határozza meg a látótávolságot. A homorú lekerekítés metszi a fényszóró sugarát az út felületén, és korlátozza a sugár hosszát. A fényszóró látótávolsága határozza meg a fényszóró sugarának a burkolat feletti magasságát és a maximális fényszórószöget az ívhossz megállapításához. A program a vezető szemmagasságát is figyelembe veszi.
A következő fényszóró-látótávolsággal kapcsolatos egyenletek homorú lekerekítések létrehozására használhatók.
ahol:
A = algebrai különbség esésszázalékban (%)
hd = a fényszóró sugarának magassága a burkolat felett lábban (vagy méterben)
L = a magassági lekerekítés hossza lábban (vagy méterben)
S = a látótávolság lábban (vagy méterben)
Ø = a fényszóró sugarának vízszintes pásztázási szöge (jellemzően 1 fok)
A következő egyenlet akkor igaz L-re, ha S kisebb, mint L:
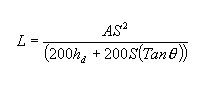
A következő egyenlet akkor igaz S-re, ha S kisebb, mint L:
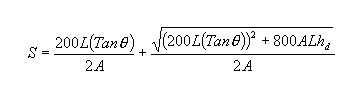
A következő egyenlet akkor igaz L-re, ha S nagyobb vagy egyenlő L-lel:
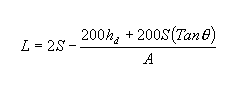
A következő egyenlet akkor igaz S-re, ha S nagyobb vagy egyenlő L-lel: