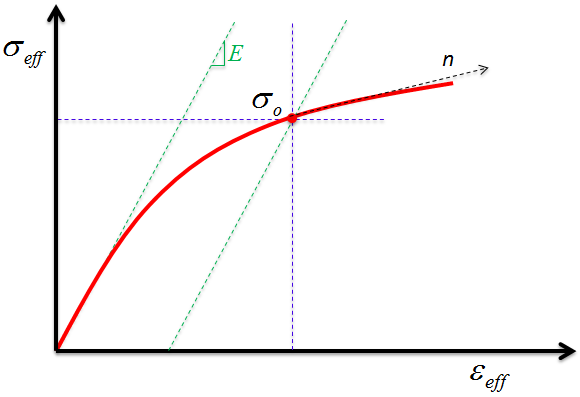
母材構成材料の応答は Ramberg-Osgood 塑性モデル[13]によって提供されます。このモデルは、予測された塑性応答が繊維方向に対する荷重方向への感度を示すことができるように拡張されたものです。母材構成材料の有効な硬化降伏強度は次の式で表すことができます。

ここで、σ0 と n は標準(等方性) Ramberg-Osgood 塑性モデルで使用される代表的な材料パラメータで、εp,eff は母材構成材料の有効な塑性ひずみです。降伏関数は、母材構成材料の有効な応力が硬化降伏強度に一致するときに満たされます。

等方性材料の場合、有効な(スカラー)応力はしばしばフォンミーゼス応力によって表されます。
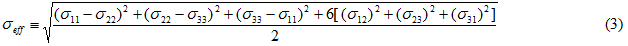
ここで、応力成分は母材構成材料の平均応力を表すものとします。有効な硬化降伏強度と同様に、有効な応力は、有効な塑性ひずみ εp,eff の関数でもあります。つまり、応力成分を計算するには母材構成材料の瞬間的な接線ヤング率 Etan が必要で、Etan は有効な塑性ひずみ εp,eff に依存します。これを以下の式に示します。

方程式 4 では、H は母材構成材料の塑性ヤング率で、以下のように εp,eff を使って表されます。

したがって、強制された全ひずみの増分中に発生する塑性の進展は、εp,eff の値を求めることで判断できるようになり、材料の状態は、展開する降伏曲面上で確認できます。すなわち、方程式 2 を εp,eff に対して繰り返し解決します。
Ramberg-Osgood モデル(方程式 1-5)では、塑性応答が等方性であると予測します。ただし、繊維位置合わせの度合の高い短繊維充填プラスチックの場合、最終破壊の前に示される塑性の度合は、強化繊維の平均方向に対する荷重の方向に大きく依存します。Ramberg-Osgood モデルは、方向依存性に対応できるように簡単に拡張できます。つまり、単に有効応力の形式を変更するだけです(方程式 3)。現在のモデルでは、修正された有効応力は次のように表されます。
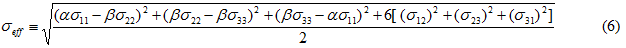
ここで、α と β は、平均繊維方向における応力成分の影響と、平均繊維方向に直交する応力成分の影響を比較して区別するために使用される重み付け係数です。この方向依存の公式では、材料応答を定義する塑性パラメータは σ0、n、α、および β です。
繊維の位置合わせの度合が比較的高い場合にのみ材料の方向依存性が強くなるということに注意してください。繊維配向がランダムの場合は、塑性応答は等方性応答に戻ります。これらの動作特性に対応するため、方向依存の重み付け係数(α および β)を定数にすることはできません。正しくは、繊維位置合わせの度合に対する関数を定数にする必要があります。現在のモデルでは、α および β は繊維位置合わせの度合に対する一次関数であると想定しています。これは繊維配向テンソルの最大固有値である λI によって定量化されます。

方程式 7 および 8 において、αm および βm はそれぞれ α および β の値で、最大の繊維配向固有値 λm,I を持つ強く位置合わせされた材料の応答特性に適合するように最適化されています。θ は、繊維配向がランダムになったときの α と β の両方の値です。λI の範囲は、完全に位置合わせされた場合の 1.0 から 3 つのすべての方向で繊維配向が完全にランダムな場合の 1/3(完全に等方性の状態)までとなります。
ただし、薄い射出成形パーツの場合、真に 3D ランダムな繊維の分布が発生することはまれです。より可能性が高いのは、薄い射出成形パーツの場合、その平面上にランダムな繊維配向を示すいくつかの場所が含まれるということです。これは、パーツの厚さ方向(すなわちλI = 1/2)には見られません。この等方性についてのより一般的な形式に対応するため、方程式 7 および 8 には係数(λI - 1/2)が含まれています。これは、λI = 1/2 の場合に、α aと β がそれぞれ同じ値 θ になり、材料の等方性が得られるようにするためです。