(次のセクションに記載されているように)ボルトの強度を決定する点応力方式は、積層破損が、積層の垂直応力が定義された穴のエッジからの距離での究極強度に達したときの張力と圧縮で開始されたとみなします[43]。これらの距離は特性長と呼ばれ、Rt および Rc です。これらの特性長は、積層材料特性および積層幅と穴の直径の関係によって異なります[44]。
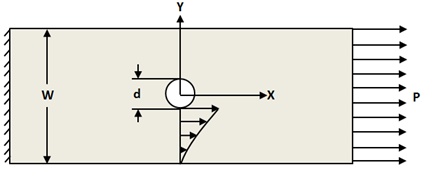
張力の特性長 Rt は、Aluko によって提唱された方式を使用して計算されます[44]。まず、エッジ荷重を受けるボルト締結ジョイントに似た、有孔試験用断片を確認します。引張応力分布 σx が以下のように平面(0,y)に沿って計算されます。
引張応力分布は、Lekhnitskii によって提唱され、後に Aluko によって円形の開口部を持つ直交異方性積層用に組み入れられた複素応力関数を使用して計算されます[45、44]。複素応力関数 φ1 および φ2 を方程式 10 および 11 に示します。垂直応力 σx は方程式 12 で定義されます[44、45]。
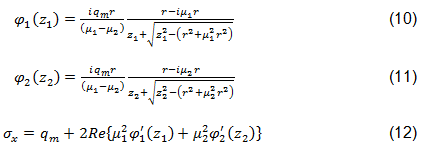
方程式 10 ~ 12 で、r は円形開口部の半径です。µ1 および µ2 は積層の直交異方性特性を定義する特性方程式の複素共役根で、方程式 13 で表されます[44]。複素変数 z1 および z2 は Aluko によって方程式 14 および 15 で定義されています。qm は無限遠で適用される応力で、方程式 16 で求められます[44]。
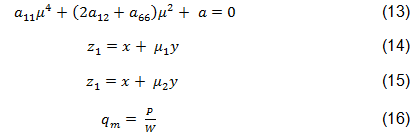
平均引張応力 σmt 間の交差の位置は方程式 17 で示され、以下のように引張応力分布 σx によって Rt の位置が定義されます。
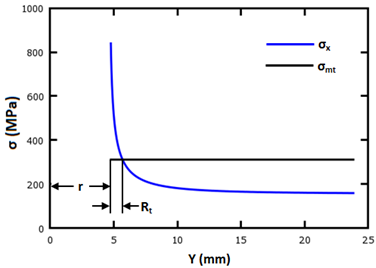
圧縮時の特性長 Rc は、Aluko の方式を使用して計算されます[44]。この方式では、支圧試験用断片が張力の場合に使用されるのと同様の方法で分析的に評価されます。支圧応力分布 σx が以下のように平面(x,0)に沿って計算されます。
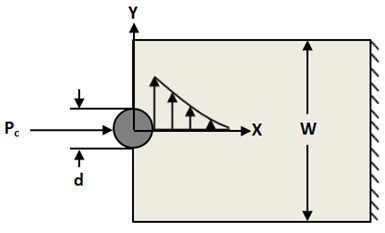
これは、円形の貫入を持つ直交異方性プレート用の Lekhnitskii および Aluko による複素応力関数を使用して行われます[45、44]。これらの式は方程式 18 ~ 20 で示されています[44]。
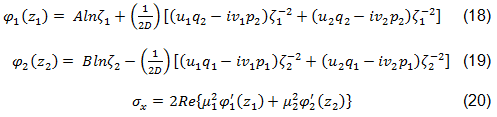
数量 u1、u2、v1、v2、q1、q2、p1、p2、D は定数で、材料特性とボルトとプレートの接触面の境界条件によって異なります[44、46]。数量 A および B は荷重、ジョイント形状、特性方程式 µ1 および µ2 の根によって異なります[44、45]。ζ1 および ζ2 は、複素平面からデカルト座標系に応力フィールドをマップする複素関数です。これらの関数は方程式 20 および 21 で求められ、符号は ζ1 および ζ2 の大きさが両方とも 1 以上になるように選択されます。
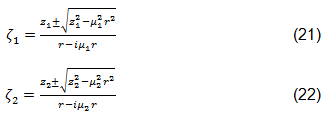
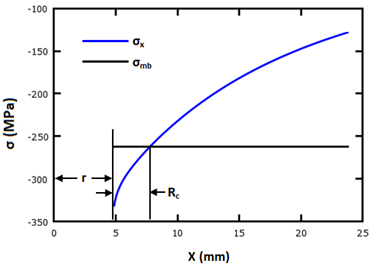
Rc の位置は、支圧応力分布 σx と平均支圧応力 σmb (方程式 23 で定義)の交差点として計算されます(任意の点荷重 Pc の影響下に含めることで試験用断片によって示されます)。

この方式の適用方法を以下に図で示します。