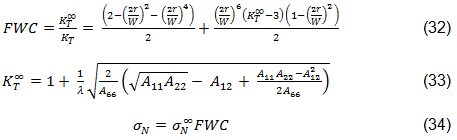特性長が決定されているので、特性カーブは方程式 24 を使用して構成されます。Chang によって提唱されたこの特性カーブを以下に示します[46]。示されているように、d は穴の直径で、θ は 0 から π の間で変動し、rc(θ)が特性カーブを定義します。このカーブは、面内積層応力が評価され、破損基準が適用されるプレート内の位置を定義します[44]。
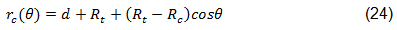
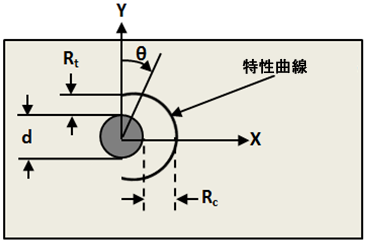
無限遠で適用される集中支持荷重 Pc および分散バイパス荷重 P の複合効果によるボルト周辺の全体の 2D 応力フィールドを予測するために重ね合わせが使用されます。これらを組み合わせた結果が Chang の特性カーブに沿って評価されます[46]。
この重ね合わせ方式で使用される複素応力関数は Lekhnitskii および Aluko によるものに基づき、方程式25 ~ 31 に示されます[45、44]。下付き文字 b および t は、それぞれ穴の埋められた解析と穴の空いた解析を示します。
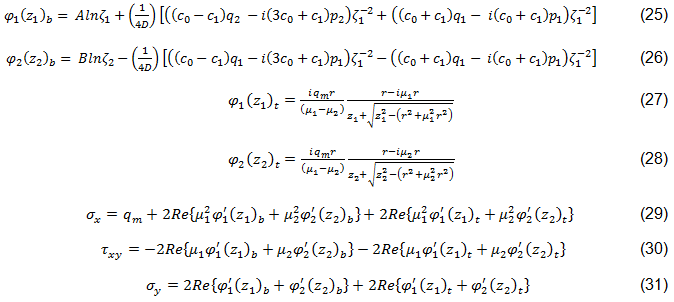
方程式 25 および 26 で、c0 および c1 は材料定数、荷重、接点境界条件によって決定されます[44]。
特性カーブに沿って予測された応力フィールドを使用して、有限幅補正係数(FWC)が方程式 32 および 33 を使用して計算されます[47、44]。KT および KT∞ は、有限幅プレートと無限幅プレートの応力集中係数を表します。A11、A12、A66 は面内積層剛性マトリックスの成分、r はプレートの穴の半径、W はプレートの幅です[44、47]。
FWC 係数は方程式 34 に示されているように適用され、ここで σN および σN∞ は有限および無限幅積層プレートの切り欠き強度です[44]。