Puck 基準(参考文献 6 と 7)は、一方向複合材料における繊維破損と繊維間破損を特定します。Puck 基準は、繊維間破損をさらに 3 つの異なる物理的モードに分離し、繊維破損をさらに 2 つの異なる物理的モードに分離します。Puck 基準の一般的なフォームは、完全な 3D 状態の応力とひずみを使用しますが、Helius Composite の実装では、古典積層理論と同様に面内応力とひずみのみを考慮します。
- 複合材料タイプ: 炭素繊維強化樹脂(CFRP)、またはガラス繊維強化樹脂(GFRP)を指定する必要があります。
- 繊維材料タイプ: マイクロメカニックス モジュール(「マイクロメカニックスで新しい積層特性を計算する」を参照)を使用して定義されていない単層材料の場合、複合材料積層で使用される繊維材料を特定する必要があります。
繊維破損
Puck 基準は、繊維破損の 2 つの異なるモードを認識します。1 つ目は引張破損で、2 つ目は圧縮「繊維よじれ」破損です。繊維の引張破損基準は、次の方程式で示します。
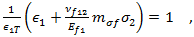
圧縮「繊維よじれ」破損は、次の方程式で示します。
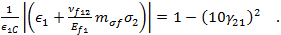
上記の繊維破損基準において、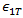
および 
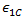は複合材料の縦方向引張および圧縮破損のそれぞれに対応する複合材料のひずみ、
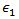は複合材料の一軸ひずみ、
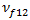は繊維の縦方向ポアソン比、
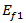は繊維の縦方向引張係数、
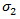は複合材料の横方向応力、
は複合材料の縦方向せん断ひずみ、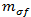
は繊維および母材における横方向応力の違いを捉えることを目的とします。炭素繊維に対しては 
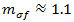で、ガラス繊維に対しては 
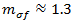です。上記の方程式において、
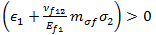の場合は引張方程式が評価され、
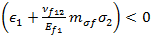の場合は圧縮基準が評価されます。
繊維間破損(母材亀裂)
Puck 基準では、繊維間破損は母材亀裂または繊維/母材はく離を含みます。Puck 基準は、モード A、B、C と呼ばれる 3 つの異なる繊維間破損モードを認識します。これらの繊維間破損モードは、強化繊維に対する破断面の方向によって識別されます。
- 繊維間破損モード A
- モード A は、0° の破断角度に対応します。この基準は、複合材料の横方向応力がゼロ(横方向荷重に対して垂直な横方向亀裂を示す)よりも大きい場合に呼び出されます。
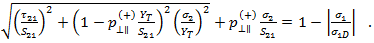
- 繊維間破損モード B
- モード B は、破断抵抗(実験定数と結合)よりも低い縦方向せん断応力を持つ横方向圧縮応力(亀裂形成を抑制)に対応します。
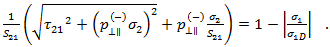
- 上記の基準は、次の場合に評価されます。
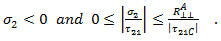
- 繊維間破損モード C
- モード C は、繊維軸に対して傾斜した面に破断を発生させるのに十分に大きな縦方向せん断応力を持つ横方向圧縮応力(亀裂形成を抑制)に対応します。古典積層理論のコンテキストにおいて、面内応力とひずみのみを含む破損の予測に対してこれは無関係であるため(また、材料特性の劣化がないため)、破断角度を定義する必要はありません。モード C の破損基準は、次のとおりです。
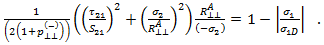
- 上記の基準は、次の場合に評価されます。
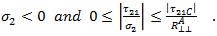
繊維間破損基準で使用される係数と用語の説明
ここでは、一般的に承認されている表記法を使用します。たとえば、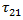
は複合材料の縦方向せん断応力、
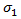は複合材料の縦方向垂直応力、 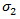は複合材料の横方向垂直応力、
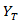は複合材料の横方向引張強度、
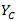は横方向圧縮強度です。
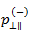と 
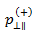は、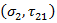
破損エンベロープの勾配です。
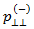と 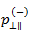間の接続を確立するには、Puck は次の関係が保持されると仮定します。
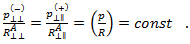
したがって、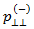 は次の方程式で求められます。
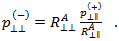
古典積層理論の面内応力とひずみのコンテキストにおいては、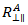
を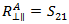 
として定義することが可能で、これにより Puck が 
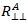を次のように表現することができます。
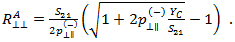
ここで、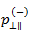 および 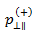の値を定義する必要があります。Puck と Mannigal (2007)は、 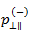と 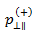に対して次の推奨値を提供しています。
また、Puck は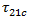 
を次のように定義しています。
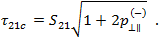
最後に、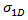
を定義する必要があります。これは、個別の繊維の繊維破損前破断を可能にする複合材料内の「劣化した」応力です。これにより、これらの領域に微小亀裂およびはく離の形でローカルの損傷が発生します。この軟化の影響を考慮するために、Puck は軟化係数 
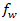によって破断抵抗(R)を劣化します。Puck はこれに対して 2 つの方程式を定義します。1 つ目の方程式は、一般化された軟化係数です。
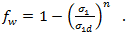
2 つ目の方程式は、破断条件を均一に維持するための軟化係数の別の式を指定するもので、応力に対して最初の次数になります。
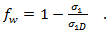
Helius Composite によって考慮される面内応力状態の場合、破断面には実行される反復計算がないため、これらの 2 つの式は同等である必要があります。したがって 、次のようになります。
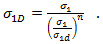
Puck の推奨事項に基づいて、Helius Composite は指数に n=6 を使用し、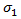 の記号に応じて 
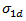を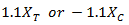 
として経験的に計算します。