このセクションでは、シェイプ ジェネレータの一連の検証に関する問題について説明します。可能な限り、シェイプ ジェネレータと既知の解または理論上の解とを照合して、どの点が確実に活用できるかを把握することが重要です。Inventor 2016 R2 - Subscription をご契約のお客様のみが使用できます。
引張立方体
この問題では、立方体の上面に張力がかかっています。立方体の底面では、4 つのコーナーが荷重の方向に拘束されています。ただし、これらのコーナーは平面で自由にスライドできます。
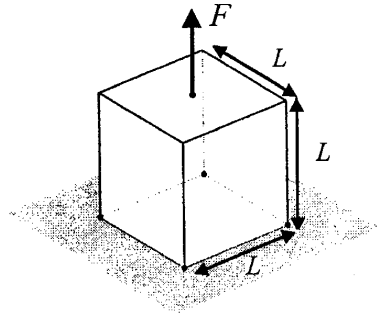

シェイプ ジェネレータを使用すると、想定される結果を再現することができます。スライド境界条件を適用した場合、立方体の底面にある水平バーは、パブリッシュされた結果と一致しています[1]。

ここで、境界条件を修正して、立方体の底面にある 4 つのコーナーで、変位をすべて固定します(均質な Dirichlet 境界条件)。次の図に示すように、形状は 4 つの対角線部材のみで構成される形状になります[1]。

片持ち梁
この問題では、梁の自由な端点上で作用する点荷重が片持ち梁(L = 40、H = 25、W = 1)にかかっています。点荷重は、梁の自由な端点の上側中央に適用されています。梁は、等方性材料で構成されており、縦弾性係数は 106、ポアソン比は 0.25 です。
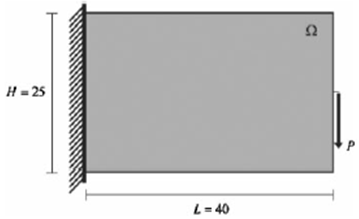
下図のパブリッシュされた結果では、最適な梁ジオメトリは、設計領域の量が元の 50% になっており、部材の最小許容直径は変動しています[2]。
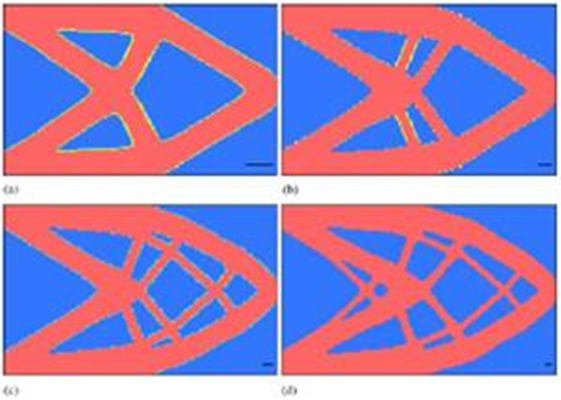
シェイプ ジェネレータを使用すると、部材の最小直径が 2 の場合(b)と非常に似た結果を再現できます。現在、シェイプ ジェネレータでは、部材の最小サイズが強制されていません。薄い部材のパーツを生成するには、下図に示すように、さらに高い解像度のメッシュを使用する必要があります。
シェイプ ジェネレータの結果と明らかな違いは、梁の固定された端部(左)に材料が残っている点です。この位置には境界条件が適用されているため、この面に沿った材料は自動的に保持されます。シェイプ ジェネレータを実行する場合、荷重および拘束を適用した面が自動的に維持されます。

ブリッジ
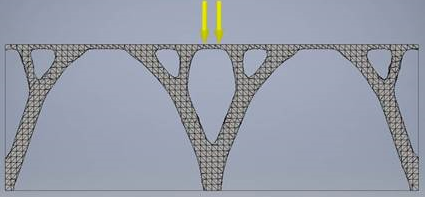
この問題の目標は、領域上で作用する均一分散荷重を支持するのに必要な支持構造物を特定することです。下図に示すように、構造物の下部には 3 つの固定拘束があります[1]。
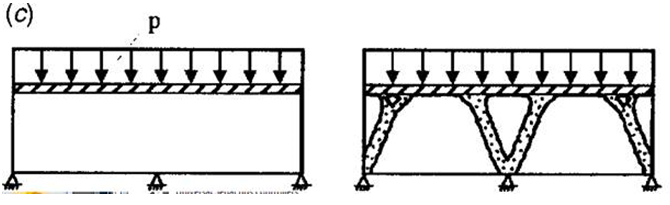
シェイプ ジェネレータを使用する場合、均一分散荷重が上面に適用されている梁として、この構造物のモデルを作成します。3 つの固定拘束は、梁の下部に適用されています。つまり、各端部の固定拘束、および中間部の固定拘束です。下図に示す結果は、パブリッシュされた解と良好に適合しています。生成された形状では、2 つの支持アーチ上に構築されたブリッジ デッキを形成しています。2 つの支持アーチにより、圧縮圧力荷重を固定拘束に伝達できます。
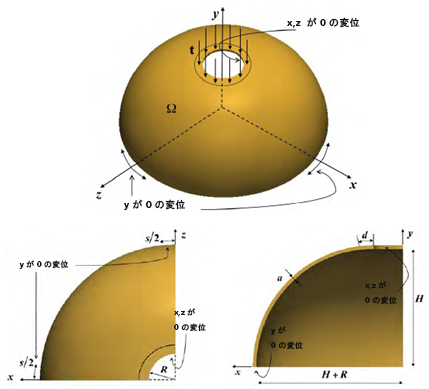
半球シェル
この問題では、薄い半球シェルを調査します。シェルの上部に開口部の穴があります。この開口部の周囲に圧力荷重が適用されています。Y 変位は、半球の下部のエッジで固定されています。X 変位と Z 変位は、半球の上部にある開口部の穴の周囲で固定されています[3]。
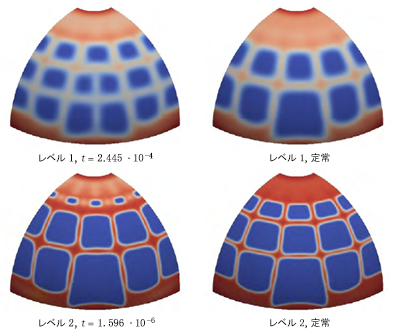

シェイプ ジェネレータを使用すると、パブリッシュされた結果を再現することができます。生成された結果のほとんどはパブリッシュされた結果に合致していますが、半球の下部のエッジに明らかな違いがあります。シェイプ ジェネレータの結果では、境界条件が適用されている箇所に材料の薄い層のみが残っています。一方、パブリッシュされた結果では、半球の下部のエッジ周辺に、厚い材料の帯が表示されています。また、パブリッシュされた結果には、対称境界条件が使用されているため、厚さが一定でない材料の帯も表示されています。
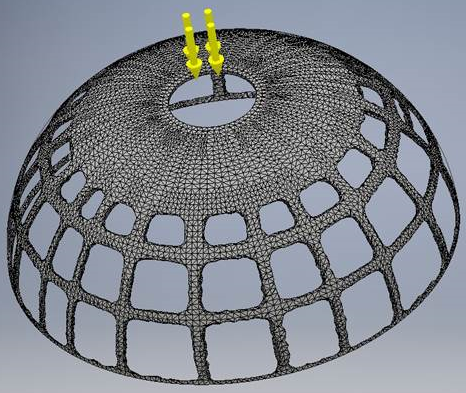
参考資料
- Eschenauer, H.A., and Olhoff, N. (2001) "Topology Optimization of Continuum Structures," Journal of Applied Mechanics Reviews. 54(4): 372.
- Guest, J.K., Prevost, J.H., and Belytschko, T. (2004) "Achieving Minimum Length Scale in Topology Optimization Using Nodal Design Variables and Projection Functions," International Journal for Numerical Methods in Engineering. 61(2): 238-254.
- Dede, L., Borden, M.J., and Hughes, T.J.R. (2012) "Isogeometric Analysis for Topology Optimization with a Phase Field Model," Archives of Computational Methods in Engineering. 19(3): 427-465.