イベント シミュレーションは、仮想研究室で物理イベントをシミュレーションするエンジニアリングです。イベント シミュレーションでエンジニアリング解析を行う場合は、古典的な応力解析とは異なる視点が必要となります。
工学の授業で、応力は力の関数 
σ= f(力)であると教わります。変形(変位)は別の力の関数 d = g(力)です。しかし、イベント シミュレーションの場合、設計における力は不確定であり、ある種の作用または運動から生じると仮定します。このシナリオにおける力および応力は、変位または変形の関数、力 = f(d)および σ = g(d)となります。変形または変位は、支配物理方程式から直接計算されます。
メカニカル イベント シミュレーションと古典的方法との対比
簡単な片持ちビームを使って、古典的な応力解析とイベント シミュレーションとの違いについて説明します。
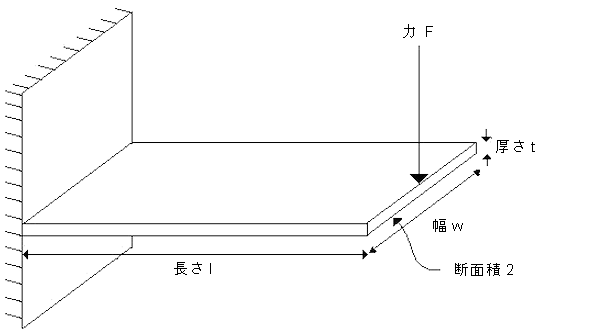
工学のハンドブックでは、片持ちビームが固定端の反対側の端部で力を受ける場合、A における最大応力は次の方程式で求められると説明されます。
|
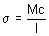
[1] |
ここで、M は力 F (M = Fl)により発生するモーメント、c は中立軸からビームの端までの距離(c = t/2)、I は領域慣性モーメント(I = wt 3 /12)です。この結果は、ビームの曲げがフックの法則(|F| = k|d|)に基づいていると考慮することで得られます。フックの法則では、力は変位の線形関数であると主張しています。この理論は、古典的な応力解析および現代の有限要素応力解析の基礎をなしています。
有限要素解析では、力のベクトル {F} の変位ベクトル {d} および剛性行列[K]について、行列方程式 {F} = [K]{d} の解が求められます。次に、方程式{σ} = E{ε} ({ε} はひずみ係数、つまり正規化された変位ベクトル)から応力を計算します。E はヤング率であり、フックの法則の定数 k に相当します。
ビームが常に静止している条件では、何の問題もありません。方程式[1]は、こうした条件でのみ有効に適用できます。しかし、機械工学の現場において、静止状態のケースを想定して設計が行われることはありません。設計では、最悪のケースのシナリオを考慮する必要があります。こうしたケースは、ビームが運動しており、力(応力)が静止状態の力よりも大きくなった場合に一般的に発生します。
ここで、イベント シミュレーションを設計プロセスに導入します。 静止状態の解を得るだけでなく、イベント全体をシミュレーションできます。イベントのシミュレーションの有益な副産物として、運動により生じる力を得ることができます。ニュートンの第二法則によると、
F=ma [2]
つまり、力は質量と加速度の積に等しくなります。質量は物体固有の特性であり、加速度は速度の変化率です。この法則では、質量が物体の動かし難さを表す物体固有の物理量であることを数値化しています。重力の影響下では、静止状態にある質量 m の物体は力 mg を生み出します(g は重力による加速度です)。等加速度(本の表紙付近の重力場)と短時間(長さ Δt)のイベントという特殊な条件の場合、方程式[2]は次のように書き換えることができます。
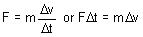
[3]
ここで、Δv は時間 Δt における速度の変化量です。0.000001 秒間に作用する 1,000,000 lb の力が生み出す力積(運動量の変化)は、1 秒間に作用する 1 lb の力と同じになります。
イベント シミュレーションは、次に示すようにニュートンの第二法則とフックの法則の組み合わせに基づいています。
F = ma = -kd または
ma + kd = 0
[4]
k の前にマイナス記号があるのは、力の方向が変位の方向と反対になるためです。また、不明瞭な量の力を排除できる点、および加速度により時間の概念が導入されている点に注目してください。現実の問題をシミュレーションするには、減衰または摩擦も考慮する必要があります。このような散逸力は次のようにモデル化できます。
F=-cv [5]
ここで、v は速度、c は定数です。散逸がどのように運動に抵抗しているかも注目してください。方程式[4]と[5]を組み合わせると、次の方程式を導出できます。
ma+cv+kd = 0 [6]
行列形式では次のようになります。
[M]{a} + [C]{v}+[K]{d} =0 [7]
これは、仮想エンジニアリングの基本方程式です。運動、減衰、および機械的変形の組み合わせがどのようにモデル化されているかに注目してください。応力に引き続き関心がある場合は、解析時に公式 {σ} = E{ε} を適用していつでも計算してみてください。公式の {ε} (ひずみ係数)は、変位ベクトル {d} から簡単に得られます。仮想エンジニアリングでは、最悪のケースのシナリオに対応した設計を行うことができます。簡単な片持ちビームの例でも、方程式[7]を解くのは手計算ではとても無理です。しかし、現代のコンピュータ テクノロジを活用することで、より複雑な問題の解を実用レベルに還元できます。
数値例
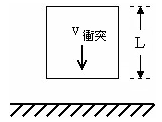
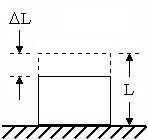
ここでは、数値例を挙げて、仮想エンジニアリングの能力を例示します。質量 m の立方体が剛体面の面上に衝突するとします。関心の対象は、この立方体で発生する最大変形です。最初に、手計算で最大圧縮長さを求めます。次に、仮想エンジニアリングで同じ問題を解き、結果を比較します。
|
接触前の立方体 |
最大変形が発生したときの立方体 |
ニュートンの第二法則により、方程式[1]で慣性前進力を求めます。古典物理学の原理に従って、立方体の質量全体は図心にあると仮定します。また、立方体の特定位置の加速度は衝突全体を通じて一定であると仮定すると、方程式[1]は次のようになります。
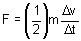
[8]
ここで、Δv は衝突期間 Δt における立方体上面の速度の変化です。方程式[8]の係数 1/2 は、方程式[1]を図心に適用するために必要となります。この場合、立方体の中程あたりに上面の半分の加速度がかかると想定します。つまり、接触の発生時に、立方体の上面が図心の 2 倍移動すると想定します。等加速度の仮定と基本運動を組み合わせることにより、衝突時における立方体の変形量を求める式が得られます。
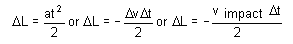
[9]
ここで、v impact は接触が発生したモーメントにおける立方体上面の速度です。方程式[9]のマイナス記号は、Δv が負の値であり、ΔL の正の値を求めているため必要になります。最大変形時に立方体の上面が移動していないため、どのように Δv を v impact に置き換えているかに注目してください。
フックの法則により、立方体の力は次の方程式で得られます。
[F=-kDL] [10]
方程式[8]～[10]を組み合わせると、次の方程式を導出できます。
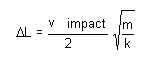
[11]
E の項に k を配置すると(面に垂直な軸に沿って立方体の長さ L が変形する場合、k = ELとなります)、次の方程式を導出できます。
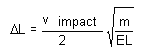
[12]
ソフトウェアを使用して、同じ衝突の問題をシミュレーションします。長さ(L) 1.0 インチ、質量(m) 0.000253 lbm の立方体をモデリングします。立方体は、ヤング率 E が 107lb/in2 の材料で構成されます。高さ 100 インチから実際に立方体が落下するイベントをシミュレーションします。その結果、衝撃速度は 278 in/sec の(vimpact)となります(強度 386.4 in/sec2 の重力場の影響がある場合)。ソフトウェアでは、最大変形を 0.000694 インチの(ΔL)と予測します。これを好意的に値 0.000699 インチ(方程式[6]により得られた値)と比較します。
この例では、簡単な衝突の問題でもデジタル プロトタイプ ソフトウェアを使用しないと、解析がいかに困難になるかを示しています。ジオメトリがさらに複雑になると、手計算がどれだけ厄介になるか、場合によっては不可能になるかを想像してみてください。従来の古典的な有限要素解析(FEA)は最終手段として使用できます。このような解析は、(全体の)運動が無視されますが、慣性前進力の知識がある場合は適切な場合もあります。不適当な側面が生じるのは、主に衝突時に力の波動により発生する振動が解析で無視されることによります。
力推定法
古典的な FEA 向けに力の値を推定する一般的な方法として、経験、剛体力学、物理的な実験の 3 つを取り上げます。
-
経験
一部のエンジニアは、類似する問題に関する過去の経験に基づいて、力を推定します。通常、安全率を基準にします。破壊の発生を防止するのに十分な安全率を設定します。ただし、慎重になりすぎて、パーツの設計が過度になる場合があります。
-
剛体力学
剛体力学のプログラムでは、パーツのモデルを使用して、運動により発生する力を計算します。力の数値を得るために、このプログラムでは曖昧に定義された剛性を使用する場合があります。このプログラムは剛体の仮定で制限されているため、剛性に基づいた力の計算は信頼できません。
-
実験
パーツのプロトタイプによる実験は、力の値を得る場合の精度の高い方法です。しかし、こうした手法は、コストの低いコンピュータ解析に完全に駆逐されています。
まとめ
イベント シミュレーションは、最小限の仮定で物理イベント全体をモデリングできます。特に、静止状態を仮定したり、運動により発生する力の値を仮定する必要がありません。さらに、イベント シミュレーションは、終了時のスナップショットだけでなく、イベントのフレームごとの記録も作成できる点でも有用性があります。