基礎励振 - 支持構造物の振動

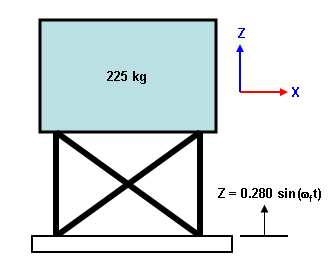
前提:基礎が運動する多自由度振動系において、物体の質量が 225 kg、支持構造物の剛性が 35000 N/m、減衰率が 0.188 であるとします。基礎は正弦振動するものとし、その振幅は 0.28 cm、振動数は系の固有振動数であるとします。

実際の構造

基礎部分はこの構造物の固有振動数で振動します。

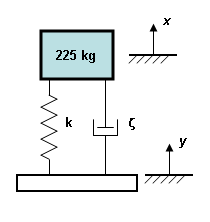
等価な模式図

k = 35000 N/m

ζ = 0.188

振動解析に関する書籍での慣例にならって、質量および基礎の絶対運動を x および y で表します。位置を時間の関数として表す場合は、斜体の x および y を使用します。

値を特定する対象:

支持構造物は、その全体を詳細にモデル化する代わりに、トラス要素で表すことができます(トラス要素の剛性 k は A*E/L で与えられることに注意)。質量は、トラスの端部に作用する集中質量として表されます。運動する基礎は固定境界条件として表され、基礎の振動は擬似的に基礎励振または基礎の加速度で表されます。質量が作用するトラス要素の端部に境界条件を与えることにより、その質量の振動を軸方向に限定します。

[ステップ]

  1. 固有値解析を実行し、固有振動数を特定します。モード解析の結果は、(問題文の指示に従って)振動数を特定することのほか、これ以降に行う 2 つのタイプの解析にも利用します。
  2. 基礎の加速度に基づく周波数応答解析を実行し、準定常状態における質量の振幅を特定します。周波数応答解析では、モデルに適用される正弦荷重がシミュレーションされます。
  3. 初速度が 0 の場合にこの系がどのような挙動を示すかを確認するため、基礎の加速度に基づく過渡応答解析(モード法)解析を実行します。過渡応答解析では、ユーザ定義の荷重曲線に基づいて、一般的な荷重に対するモデルの応答が計算されます。過渡状態において、より大きなたわみが生じるかどうかに注目します。

モデルを作成する:

  1. FEA モデルを新規に作成します。
    1. 解析タイプを[線形]: [固有値解析 (モーダル)]に設定します。
    2. 振動を記述する単位にセンチメートルが使用されている場合は、モデルに対する単位として、ニュートン、センチメートル、および秒を選択します。[既定の単位をオーバーライド]をクリックし、[単位系]ドロップダウンを[カスタマイズ]に設定した後、[力]、[長さ]、および[時間]のそれぞれに対応する単位を、[N]、[センチメートル(cm)]、および[秒]に設定します。[OK]をクリックして単位を設定します。
    3. [新規]をクリックし、モデルの名前を入力します。
  2. [作成][作成][ライン]を使用して、支持構造物を表すラインを追加します。[構造体として使用]チェック ボックスがオフになっていることを確認します。トラス要素は 3D であるため描画の向きは任意ですが、整合性を保つためにも、既存イメージの向きに合わせることをお勧めします。剛性の値 A*E/L が適切である限り、要素の長さは任意ですが、ここでは長さとして 2 cm を選択することをお勧めします。始点を(0,0,0)、次の端点を(0,0,2)としてラインを描画します。ダイアログ ボックスを閉じます。
  3. [表示][ナビゲーション][全体表示]を使用してモデル全体を全体表示します。
  4. 要素タイプをトラスに設定します。ツリー表示で、[要素タイプ]をクリックし、[トラス]を選択します。
  5. [要素定義]を使用してトラスのプロパティを設定します。[要素定義]を右クリックし、[要素定義を編集]を選択します。断面積の値は任意に設定できます。ここでは 1 cm 2 と入力し、[OK]をクリックします。
  6. 特に質量に関する項についての入力をより簡単にするため、[表示単位系]に質量の単位として kg を指定します。
    1. ツリー表示の上部にある[単位系]を右クリックし、[新規]を選択します。
    2. [単位系]ドロップダウン メニューを[カスタマイズ]に設定し、[力]、[長さ]、[時間]、および[質量]のそれぞれに対応する単位を、[N]、[センチメートル(cm)]、[秒]、および[キログラム(kg)]に設定します。
    3. [説明]には、簡単に「N cm kg」と入力します。
    4. [OK]をクリックして、[表示単位系]の設定内容をアクティブにします。
  7. 材料特性を入力します。ツリー表示で、[材料]を右クリックし、[材料を編集]コマンドを選択します。要素の長さおよび断面積は既に設定されているため、材料特性を無作為に選択することはできません。適切な剛性を設定するためには、ヤング率を 700 N/cm 2 にする必要があります。[k = 35000 N/m = 350 N/cm = A*E/L = (1 cm 2 )*(700 N/cm 2 )/(2 cm)] [ユーザ定義]というエントリを選択し、[プロパティを編集]をクリックします。[ヤング率]に 700N/cm 2 と入力します。また、要素内の質量が 0 になり解を求める際に問題が生じないようにするため、質量密度として 0.05 kg/cm 3 と入力します。この値と、既に選択した長さおよび断面積から、要素の合計質量は 1 kg となります。これは、適用されている質量 225 kg に比べると、非常に小さな値です。[OK]を 2 回クリックし、特性を設定します。
  8. モデルに境界条件を追加します。バネ下部の頂点を選択し([選択][形状][点または長方形]および[選択][選択][頂点])、右クリックして、[追加][節点境界条件]を選択します。[ピン拘束]をクリックして、節点を X、Y、および Z の並進移動(Tx, Ty, Tz)に固定します。[OK]をクリックして、境界条件を適用します。(トラス要素には回転の自由度がないため、この状況では[固定]という境界条件でも適用することができます)。
  9. バネ上部の頂点を選択し([選択][形状][点または長方形]および[選択][選択][頂点])、右クリックして、[追加][節点境界条件]を選択します。バネは、軸(Z)方向には自由に移動できる必要がありますが、転倒はしないようにする必要があります。[Tx]チェック ボックスおよび[Ty]チェック ボックスをオンにします。[OK]をクリックして、境界条件を適用します。
  10. 上部の頂点を選択した状態で、構造の質量を追加します。右クリックして、[追加][節点集中質量]を選択します。[質量単位]オプションが選択されていることを確認した上で、[X方向]の質量(キログラム単位)として 225 を入力します。(質量が 3 つの方向すべてに対して一様に作用するよう、[一様]チェック ボックスはオンしておく必要があります)。[OK]をクリックして、集中質量を適用します。
  11. 図に示されているように、このモデルには節点が 1 つしかなく、しかもその節点は 1 方向にしか移動できません(Z 移動)。つまり、自由度は 1 です。ここでは詳しい理由を説明することはできませんが、このモデルは小さ過ぎるため、FEA で解を求めることはできません。解を求めるためには、このモデルにさらにいくつかの自由度(または方程式)が必要です。そこで、ラインを選択し([選択][形状] [点または長方形]および[選択][選択][ライン])、それを 4 つに分割します([作成][修正][分割][4][OK])。これにより、使用するソルバーに対して 3 つの節点が新たに作成されます。このとき、これらの節点が移動できる方向を軸方向に限定する必要があります。節点の周囲にあるボックスをドラッグして頂点を選択し([選択][形状][長方形]および[選択][選択][頂点])、右クリックして、[追加][節点境界条件]を選択します。ダイアログ ウィンドウのタイトル バーに、節点境界条件オブジェクトを作成中であるという内容のメッセージが表示されます。[Tx]チェック ボックスおよび[Ty]チェック ボックスをオンにします。[OK]をクリックして、境界条件を適用します。
  1. モード解析の実行前に行う最後の作業として、モードおよび周波数の個数を表す解析パラメータを設定します。[設定][モデル設定][パラメータ]を選択し、[計算する周波数の数]/[計算するモードの数]に 1 を入力します。[OK]をクリックします。(作成したモデルは自由度が 1 であるため、計算する周波数はただ 1 つです。)

手順 1: 固有値解析を実行する

  1. [解析][解析][シミュレーションを実行]コマンドを使用して解析を実行します。解析が完了すると、結果環境にモデルが表示されます。固有振動数 1.985 cycles/sec を記録しておきます。

手順 2: 周波数応答解析を実行する

  1. [FEA エディタ]タブに戻ります。
  2. 基礎の振動に伴う定常たわみを計算するため、解析タイプを[周波数応答解析]に設定します([解析][変更][タイプ][線形][周波数応答解析])。新しい設計シナリオにモデルをコピーするかどうかを確認するプロンプトが表示されたら、[はい]をクリックします。固有値解析の結果は[設計シナリオ 1]に、周波数応答解析の結果は[設計シナリオ 2]にそれぞれ表示されます。また[設計シナリオ]を選択すれば、どちらの結果にも瞬時にアクセスできます。
  3. この解析タイプの場合、入力値はすべて[解析パラメーター]を介して入力されます。[設定][モデル設定][パラメータ]を選択し、[解析設定]をクリックします。([出力コントロール]にある各オプションは、テキストベースの出力を追加的に取得する場合にのみ使用するためのものです。通常はアクティブにしておく必要はありません。)4 つのタブで、荷重の定義をすべて入力します。これら複数のタブで入力する内容をまとめると次のようになります。
    1. [励振される節点]タブでは、荷重位置を指定します。ただし荷重の周波数および振幅は、このタブでは指定しません。その代わり、[励振周波数定義のインデックス]を指定することにより、荷重位置を強制周波数に関連付けることができます。(ただし、他のタブでの入力を先に行い、[励振される節点]タブへの入力を最後に行った方がよい場合もあります。)
    2. [励振周波数]タブでは、励振の周波数を指定します。ただし荷重の振幅は、このタブでは指定しません。そのため、正弦波スイープ試験を近似的に実行する場合は、このタブで複数の行に強制周波数を最小値から最大値まで f 間隔で入力します。
    3. [減衰率]タブでは、モデルの減衰について入力します。このテーブルを各励振周波数で補間することにより、各強制周波数での減衰率が特定されます。そのためこのテーブル内の周波数は、励振周波数テーブルの内容と一致する必要はありませんが、励振周波数の全範囲を網羅していることが必要です。
    4. [振幅]タブでは、適用されている荷重の振幅を入力します。このテーブルを各励振周波数で補間することにより、各強制周波数での正弦荷重の大きさが特定されます。そのためこのテーブル内の周波数は、励振周波数テーブルの内容と一致する必要はありませんが、励振周波数の全範囲を網羅していることが必要です。
  4. 周波数応答解析にはモード解析の結果が使用されるため、[設計シナリオの固有値解析結果を使用]フィールドに 1 を入力します。
  5. [励振される節点]タブで、モデル内での正弦荷重の位置を定義します。この例題では次のように設定します。
    1. 基礎の支持構造物が振動することを指定するため、[節点番号]領域で[基礎励振]オプションを選択します。
    2. 荷重は基礎の加速度であるため、[励振のタイプ]は[力入力]ではなく[加速度の入力]であることが必要です。
    3. [励起の方向]領域で、基礎が振動する方向として[Z 方向]オプションを選択します。モデル内で移動が Z 方向に限定されている節点はいずれも、基礎に取り付けられているとみなされるため、振動することになります。
    4. [振幅スケール係数]に 1 と入力します。この値により、適用される荷重が増減します。
  6. [励振周波数]タブで、モデルが振動する際の周波数を定義します。この例題では、テーブルに入力する必要がある周波数は 1.985 Hz のみです。
  7. [減衰率]タブで、減衰率を周波数の関数として定義します。テーブルに入力されている行が 1 つだけの場合は、すべての強制周波数に対して減衰が一定となります。そのため、周波数 1 Hz、減衰率 0.188(問題文に記されている値)を入力します。
  8. [振幅]タブで、適用されている荷重の大きさ(加速度または力)を、周波数の関数として定義します。このモデルでは基礎の加速度が使用されますが、問題文では基礎運動の振幅が与えられています。加速度を求めるためには、変位(y = 0.280*sin(ωt))の 2 次導関数を求め、加速度の式(ay = -0.280*ω2*sin(ωt))を導きます。ここから計算される加速度振幅は、(0.280 cm)*[(1.985 cycles/sec)*(2*pi radian/cycle)]2 = 43.55 cm/sec2 となります。インタフェースでは、重力加速度 G を単位とした加速度が使用されるため、加速度振幅を重力定数で割って (43.55 cm/sec2)/(981 cm/sec2) = 0.0444 G を求める必要があります。適用されているすべての周波数に対して荷重が一定の場合、入力する行は 1 つのみです。[周波数]に 1、[加速度]に 0.0444 と入力します。(モデルに力が適用されていなければ、[力]列は空欄のままで構いません。)
  9. [OK]を 2 回クリックし、解析パラメータを適用します。
  10. [解析][解析][シミュレーションを実行]コマンドを使用して解析を実行します。解析が完了すると、結果環境にモデルが表示されます。
  11. 結果として表示される変位は相対変位です。(基礎の変位は、入力した振幅 0.280 cm ではなく 0 として表示されることに注意してください。)このモデルは移動が Z 方向に限定されているため、変位の大きさの結果は Z 変位の結果と同じ値ですが、プレゼンテーション用としては Z 変位の結果を使用した方が良い場合もあります。その時は、[結果コンター][変位][Z]コマンドを使用します。
  12. 周波数応答解析に対しては、同相、異相、および SRSS での結果がそれぞれ得られます。[結果オプション][解析指定][応答タイプ]ドロップダウン メニューを使用して、それぞれのタイプを表示します。この例題では、同相成分は実質的に 0 であるため、異相での結果と SRSS での結果は同じです。質量は、基礎を基準として最大で 0.745 cm 移動します。
  13. 質量の絶対変位は、次のように計算することができます。(使用する記号については、図 1 を参照してください。時刻 t における絶対位置は x、y、z で表し、1 周期における最大値または最大振幅は X、Y、Z で表します。) 
    Relative displacement z               =  x - y
Absolute displacement x               =  z + y
The motion of the base is given as y  =  Y*sin(ωt)
and the relative displacement z       =  Z*sin(ωt-φ), where φ is the phase angle.

Thus, x                               =  Z*sin(ωt-φ) + Y*sin(ωt)

    周波数応答解析の要約ファイル(レポート環境からアクセス可能)から、計算された位相角は元々 90 度(下記参照)なので、 

    x  =   Z*sin(ωt-φ) + Y*sin(ωt)
   =   Z*sin(ωt-90) + Y*sin(ωt)
   =  -Z*cos(ωt) + Y*sin(ωt)

位相が異なるため、x の最大変位 X は Y+Z にはなりません。最後の式は x = X*sin(ωt + φ)と書き換えることができます。ただし、X = sqrt(Z2 + Y2)は最大変位、φ は位相角です。よって、Z = 0.745 cm、Y = 0.280 cm で、質量の絶対変位は 0.796 cm となります。

周波数応答解析の概要ファイルから抜粋: 

 START OF LOAD 1
 Applied frequency case #  1  (Applied frequency = 1.985E+00 Hx)
 Mode No.                  Phase Angel (Deg.)     Amplitude
 1                         8.9934E+01             1.1172E+00

手順 3: 時間履歴解析を実行する

  1. [FEA エディタ]タブに戻ります([ツール][環境][FEA エディタ])。
  2. 基礎の振動による過渡たわみを計算するため、解析タイプを過渡応答解析に設定します([解析][変更][タイプ][線形][過渡応答解析(モード法)])。新しい設計シナリオにモデルをコピーするかどうかを確認するプロンプトが表示されたら、[はい]をクリックします。過渡応答の結果は[設計シナリオ 3]に表示されます。
  3. これまでと同様に、[解析パラメーター]で基礎励振を定義します( [設定][モデル設定][パラメータ] )。
  4. 運動していない状態から準定常状態に至るまでに何周期を要するかは分かっていません。仮に 10 周期必要だとすると、時間は 5 秒あれば十分です(= (10 cycles)/(2 cycles/sec))。1 周期における結果を正確に捉えるため、その周期を 50 個のステップに分割します。この場合、各時間ステップのサイズは 1/[(2 cycles/sec)*(50 steps/cycle)] = 0.01 秒となります。[時間ステップ数]に 500、[時間ステップサイズ]に 0.01 と入力します。
  5. 基礎運動に対する荷重曲線を定義します。[荷重曲線]をクリックします。[時間]および[係数]から成る荷重曲線テーブルに値を入力する必要があります。ただし係数は、基礎の加速度(単位は cm/sec2)です。既に計算したとおり、基礎の加速度の大きさは 43.55 cm/sec2 であるので、基礎の加速度を表す式は (43.55 cm/sec2)*sin(1.985 Hz * (2pi radian/cycle) * 時間) となります。個々の時間ステップに対して値を入力する代わりに、スプレッドシートを使用して計算を行い、その結果をカンマ区切り(CSV)ファイルとして保存し、それを荷重曲線にインポートすることができます。この方法を使用すると、Autodesk Simulation インストール フォルダの Models サブフォルダ内にファイルが作成されます。そのためには、[荷重曲線入力]ダイアログで[インポート]をクリックします。[閲覧]をクリックし、43.55sine.csv というファイルを選択して、[開く]をクリックします。ファイルの内容が画面に表示されます。最初の行はデータを識別する指標となるため、[最初の行を省略]の値として 1 を入力します。[インポート]をクリックして、処理を完了します。正弦関数で表される荷重曲線が表示されます。[OK]をクリックして、[荷重曲線入力]ダイアログ ボックスを閉じます。
  6. [減衰係数(臨界値の割合)]には、問題文にあるとおり 0.188 と入力します。
  7. この例題では基礎の加速度を使用するため、節点荷重を適用する場合に使用する[荷重]タブは必要ありません。[オプション]タブで、[基礎励振タイプ]を[並進運動]に設定します。
  8. [設定]をクリックして、基礎励振に関するパラメータを指定します。具体的には、[Z 方向]に対する[荷重曲線]を[荷重曲線 1]に設定し、[加速度の大きさ]を 1 cm/s2 に設定します(加速度の大きさを 1 に設定するのは、荷重曲線により最大値が与えられるためです)。[OK]をクリックして、[基礎励振の設定]ダイアログを閉じます。
  9. 過渡応答解析には、モード解析の結果が使用されるため、[設計シナリオの固有値解析結果を使用]フィールドに 1 を入力します。
  10. [OK]をクリックして、[解析パラメーター]を閉じます。モデルの準備が完了し、いつでも解析を開始できます。[解析][解析][シミュレーションを実行]をクリックします。
  11. 解析が完了すると、結果環境にモデルが表示されます。結果には500 個の時間ステップがあり、時間ステップごとに計算を行うことで、結果を確認できます。ただし、時間ステップを 1 つずつ追いながら結果を確認するよりも、結果全体をプロットする方が重要です。
  12. 結果のタイプを Z 変位に設定します([結果コンター][変位][Z])。
  13. 集中質量が作用する節点を選択します([選択][形状][点または長方形]および[選択][選択][節点]を選択後、モデルの上部にある節点をクリックします)。右クリックして、[グラフの値]を選択します。これにより、第 2 のプレゼンテーション ウィンドウが作成され、そこにグラフが表示されます。結果は図 2 のように表示されます。準定常状態には、約 5 周期で達します。目視で確認すると、支持構造物を基準とした質量の予想変位は 0.75 cm 前後と判断できます。
  14. ツリー表示でのクリック操作により、コンター ウィンドウ[プレゼンテーション 1 <未指定>]に戻ります。4 秒付近の時間ステップで変位が最大になっていると考えられるため、そこで変位の実際の値を確認します。[結果コンター][荷重ケース オプション][荷重ケース][設定]を選択した後、値として 400 を入力し、[OK]をクリックします。前後いくつかの時間ステップを移動しながら([結果コンター][荷重ケース オプション][次へ]または[戻る])、変位が最大であるステップを特定します。ステップ 403 で、変位の値 0.742 cm が確認できます。

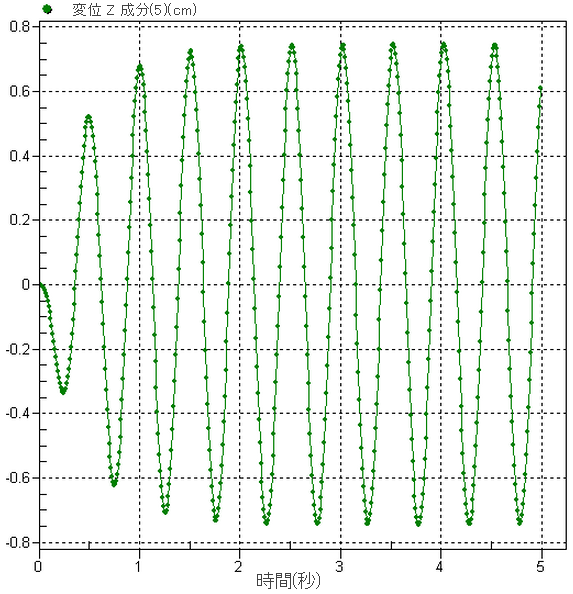
図 2: 質量の変位のプロット

モデルおよび結果のアーカイブ(ground motion.ach)は、Autodesk Simulation インストール ディレクトリの Models サブフォルダに保存されます。

この例題については、振動解析に関する数多くの書籍に記載されている方法を用いて解を求めることができます。この例題は、『Vibration Analysis 第 2 版』(著者 Robert K. Vierck、発行者 Harper & Row)の「例 4-9」(129～130 ページ)を参考にしたものです。

親トピック: 線形静解析と応答解析