すべてのモデル対して正しい解法を提供する接触パラメータの値の組み合わせは 1 つではないため、ユーザは、それぞれのパラメータの機能を十分に理解して、所定の問題に対する適切な値のセットを判別する必要があります。
接触パラメータは、ペアごとに個別にカスタマイズできます。ツリービューで接触ペアを選択し、右クックから[設定]を選択してください。 または、メインの[MES: サーフェス間接触]ダイアログ ボックス(スプレッドシート)から、目的のペアの[パラメータ]列をクリックしてください。 いずれの方法でも、[接触ペアのコントロールとパラメータ]ダイアログ ボックスに移動します(パラメータが変更されているペアは、[パラメータ]列の[カスタム]に表示されます。それ以外は、[パラメータ]に既定が表示されます)。
[接触ペアのコントロールとパラメータ]ダイアログ ボックス
接触問題タイプ
[接触問題タイプ]ドロップダウン ボックスで、解析中に常に生じる可能性のある接触の一般的なタイプを選択してください。 この選択により、接触剛性の自動計算の動作がコントロールされます。選択対象が明らかな場合もありますが、状況が低速であるか高速であるかが明確でないこともあります。 その違いは、解法の効率の問題です。 いずれの選択でも、正しい結果が得られます。使用可能なオプションは次のとおりです。
- [低速接触(圧着)]: ペア間の接触の特徴は、パーツがゆっくと接触にいたる(低速)場合と、パーツが連続的に接触している状態(プレスフィット)があります。適用される接触剛性のルーチンは使用できますが、既定では使用されません。
- [高速接触(衝突)]: ペア間の接触の特徴は、衝撃試験や落下試験など、急激な変化が生じることです。適用される接触剛性のルーチンは、既定では使用されません。
接触法
[接触法]ドロップダウン ボックスで、選択した接触ペアに使用する接触方式を選択してください。オプションは次のとおりです。
- [摩擦なしの接触]: この接触方式では、接触サーフェスにおいて、パーツが相互の間で大きな相対運動を受けることができます。 パーツは、その事象の期間を通じて接触状態に移行することや、接触状態から離れることができます。サーフェス間の運動に抵抗する摩擦はありません。これが最も一般的な接触方式です。
- [摩擦のある接触]: この接触方式は、サーフェス間のすべり運動に抵抗する摩擦を定義することができる以外、摩擦のない接触と同じです。定義する必要のある係数は、[摩擦のモデル化]セクションで指定した[摩擦則]設定に応じて変化します。
- [摩擦のないすべり/はね上がりのない接触]: この接触方式では、接触が起こるまで 2 つのサーフェスが自由に移動できます。また、引張りを受けても、節点は分離しません。接線の方向は、独立して拘束できます。接触中のパーツのすべりを停止する場合は、[すべり無し]チェック ボックス([スライド/バウンド無し 接触オプション]セクション)を使用してください。その場合、接触しているパーツは連結されます。一方、[すべりなし]チェック ボックスがアクティブ化されていない場合、サーフェスは互いに自由にすべることができます。[すべりなし]オプションがアクティブ化されていない場合、サーフェスは別々にすべることができる点に注意してください。
- [摩擦のないすべり/はね上がりのない接触]: この接触タイプは、上述の「すべりあり / バウンスなし」とよく似ています。違いは、サーフェスが接触状態になった後に、摩擦が含まれる点です。静摩擦係数およびすべり摩擦係数は、[摩擦のモデル化]セクションで定義することができます。上述の「摩擦のある接触」の説明を参照してください。 注: [スライド/バウンド無し 接触オプション]セクションの[はね上がりなし]チェックボックスは常にオンになっていて、変更することはできません。[はね上がりなし]の制限は、[接触法]ドロップダウン ボックスで、2 つの[はね上がりのない接触]のオプションのうちの 1 つが選択されている場合にのみ適用されます。このチェック ボックスは、その他の接触法では無視されます。
- [結合接触]: この方法は、不一致の節点を含むサーフェス間の接着接触をシミュレーションするために使用されます。この接触方式を選択し、サーフェスの初期状態が指定距離以内の場合、これらのサーフェスは永続的に結合されているとみなされ、引張りを受けても、事象の間に分離することやすべることはありません。サーフェス間の距離が指定距離より大きい場合には、接触とみなされません。指定距離は、[結合接触オプション]セクションを使用してコントロールできます。 [タイドコンタクトの初期干渉]チェック ボックスがオンになっていない場合、サーフェス間の初期距離が接触距離として使用されます。 このチェック ボックスがオンになっている場合は、距離を[タイドコンタクトの距離]フィールドに入力する必要があります。この接触方式を使用する解析は、サーフェス上の節点が一致する解析より低速になります。 注: サーフェス上の節点の 3 つの並進(Tx, Ty, Tz)のみが連結され、回転は連結されません。したがって、ブリック パーツの面からシェル要素が突き出た構成(シェルで作られた片持ちビームなど)においては、シェルとブリックの間で結合接続のみが使用される場合、シェル パーツはブリックの支持部で自由に回転することができます。
接触タイプ
[接触タイプ]ドロップダウン ボックスで、選択した接触ペアに使用する接触のタイプを選択します。
接触をサーフェス間であると説明するのは、誤解を招く恐れがあります。実際には、2 番目のパーツ/サーフェス上の節点が、1 番目のパーツ/サーフェス上の節点と連結されるため、節点がサーフェスを通過することはありません。 必要に応じて、逆は真になります。1 番目のパーツ/サーフェス上の節点を、2 番目のパーツ/サーフェスのサーフェスに連結することができます。どのような場合にも、1 つのパーツのサーフェスが 2 番目のパーツのサーフェスを通過するのを妨げられることはありません。
[接触タイプ]のオプションは次のとおりです。
- 自動: 既定の方式では、関連する接触サーフェス(メッシュ)と材料モデルに基づいて、[点サーフェス間]と[サーフェス間]の接触タイプから自動的に選択されます。また、プライマリ サーフェスとして機能するサーフェスも自動的に決定されます(解析の開始前に、1 番目と 2 番目のパーツ/サーフェスが交換されることもあります)。 ただし、[自動]オプションでは、解析中に大きな変形を生ずる場合には、最適な接触タイプが選択されないことがあります。 その場合には、[自動]オプションで実行された設定の妥当性を確認してください。選択された接触のタイプは、ログ ファイルに一覧表示されています(各パーツ内の要素数の一覧も含まれます)。
- サーフェス間: このオプションは、セカンダリ パーツ上の節点が、プライマリ パーツのサーフェスを通過しようとするときや、その逆のときに接触が生じることを示しています。プライマリ パーツ上の節点は、セカンダリ パーツのサーフェスに接触することができます。
- 点サーフェス間: このオプションは、2 次パーツ上の節点が、1 次パーツのサーフェスを通過しようとするときに接触が生じることを示しています。プライマリ パーツ/サーフェス上の節点は、セカンダリ サーフェスを通過することができます。
- 点間: この方式は、2 つのサーフェスが、相互に比較して無視できるようなすべりを受ける状況に最適です。 このオプションは、セカンダリ パーツ上の節点が、プライマリ パーツ上の節点を通過しようとするときに接触が生じることを示しています。プライマリ パーツの節点とサーフェスとの間の接触は検出されません。パーツがどのように移動するかには無関係に、常に接触力は連結された節点の元のペアの間にあります。 点間接触が作成されると、[結果]環境には、モデルの余分なパーツ(点間接触の各ペアに対する接触要素の一部)が表示されます。
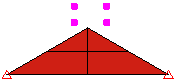
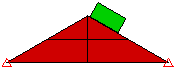
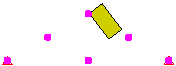
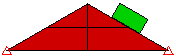
点サーフェス間の接触方式は高速ですが、1 次パーツの点は、2 次パーツのサーフェスを通過する可能性があることを理解しておく必要があります。この接触は検出されません。 サーフェス間接触は、接触の検出性に優れていますが、その代償として、より多くの接触要素が生成されます。すなわち、ターゲット パーツ/サーフェス上の節点は、マスター パーツ/サーフェス上の節点によって定義されるサーフェスを通過できず(点とサーフェス間の接触とまったく同様)、マスター パーツ/サーフェス上の節点は、ターゲット パーツ/サーフェス上のサーフェスを通過できないことを示しています。図 2 を参照してください。
|
サーフェス間接触
|
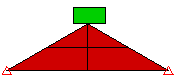
点とサーフェス間の接触 (くさび上の点)
|
点とサーフェス間の接触 (ブロック上の点)
|
|
Time = 0 |
||
|
等価なシステム。 両方のパーツのサーフェスは、接触を介して連結されています。 |
等価なシステム。 接触が連結されている限り、くさび上の節点のみが存在します。 |
等価なシステム。 接触が連結されている限り、ブロック上の節点のみが存在します。 |
| Time = 0.024 秒 | ||
|
ブロック上のサーフェスが、くさびのサーフェス/節点に接触します。 |
ブロック上のサーフェスが、くさびの節点に接触します。 |
ブロックの節点がくさびのサーフェスに接触するまで、接触は起こりません。くさびは、ブロックを通過します。 |
| Time = 0.12 秒 | ||
|
ブロック上のサーフェスが、くさびのサーフェスをすべり落ちます。 |
ブロックは、くさびの節点の間を通過します。 |
ブロックは、くさびに突き刺さります。 |
| Time = 0.15 秒 | ||
|
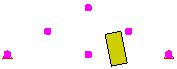
|
|
|
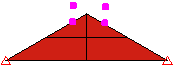
図 1: 接触タイプの比較 くさび上にブロックを落下させる 3 種類のモデル。それぞれのモデルでは、接触タイプが異なります。 |
||
接触ペアのサーフェスの 1 つがシェル要素のパーツ上にある場合、接触ペアに関連するシェルの側面を選択してください(上面は、[要素定義]ダイアログ ボックスで定義された要素の垂直点の逆側です)。2 つの物体が指定方向から接近する場合にのみ接触は起こります。たとえば、シェルのトップで接触が起こるように指定する場合、2 番目の物体がトップからボトムの方向に移動するときに接触が起こります。2 番目の物体がボトムからトップ方向に移動する場合には、接触は起こりません。これの可視化方法がもう 1 つあります。2 番目のオブジェクトは、シェルの外側から接近するときにのみ、選択された側面(トップまたはボトムのいずれか)と接触します。このオブジェクトは、選択された側面に到達するためにシェルを通過する場合、接触を検出しません。図 3 を参照してください。
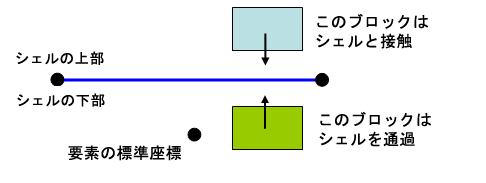
図 2: シェルのトップと接触するように定義された 2 つのブロック
ライン要素(ビーム、トラス)との接触では、ライン要素上の節点が最初のパーツ/サーフェスと接触している場合にのみ、接触が検出されます。また、線要素上のすべての節点を接触に考慮するか([すべて線要素上])、または端部の節点のみを考慮するか([要素の終端のみ])を、[接触している節点]ドロップダウン ボックスで指定してください。 たとえば、歯ブラシの毛はビーム要素で構成されており、毛の先端の節点と歯の接触のみが必要とされます。要素の先端の節点のみが使用されます。しかし、トラス要素で構成される安全防止ネットは、ネット上のすべての節点と落下物との間の接触を検出する必要があります。ライン要素上のすべての節点が使用されます。
[摩擦のモデル化]セクション
摩擦のない接触の場合、要素剛性マトリックスは対称です。 摩擦が含められると、マトリックスは非対称になります。非対称のソルバを使用すると、通常の対称ソルバーを使用する場合よりも計算コストが高くなります。効率を考慮して、MES では強制的に要素剛性を対称とし、摩擦のある接触に対称ソルバーを使用できるようになっています。
解析で摩擦のある接触を考慮する場合、解法プロセスは、すべりのプロセスからの影響を非常に受けやすくなります。 接触サーフェスがすべりを開始すると、すべり前の平衡状態は有効でなくなり、プロセッサでは、解法プロセス中に新しい平衡状態を探す必要があります。さらに、対称の近似により、収束性に乏しい可能性があります。使用可能な摩擦則の各オプションは、ソリューションが不安定になることをさまざまな方法でコントロールしようとします。
Simulation Mechanical には、非線形のサーフェス間接触に対して 3 つの摩擦則の選択肢があります。
- 修正されたクーロン摩擦
- 粘性摩擦のあるクーロン
- クーロン摩擦を平滑化
これらの摩擦則のそれぞれとそれに適用されるパラメータは、以下のサブセクションで説明しています。
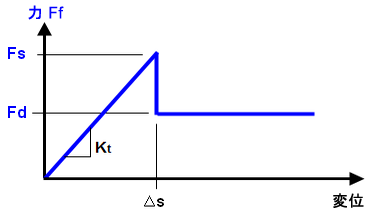
修正されたクーロン摩擦
この摩擦則は、古典的な摩擦アルゴリズム「クーロン摩擦」を使用します。基本的なクーロン摩擦モデルにおいては、2 つの接触サーフェスが所定の大きさまでのせん断応力に抵抗することができます。この大きさは、摩擦係数と、相対すべり運動を受ける前の垂線方向の接触圧から決定されます。クローン摩擦モデルは、τ = μP と定義されます。ここで、μ は摩擦係数、P は法線方向の接触圧です。サーフェス間接触では、静摩擦係数(μs)と動摩擦係数(μd)を定義することができます。理想状態では、静摩擦係数から得られた μsP をせん断応力が超えた後、2 つのサーフェスがすべりを開始します。さらに、せん断応力は動摩擦係数を使用した μdP になります。
理想状態(せん断応力が静的な値を超えるまで運動なし)を数値的に達成するのは、図 3 に示すように困難です。そのため、この摩擦則の使用時に[接線の剛性比率]が定義されます。接線方向の剛性比とは、法線方向の接触剛性(K)に対する、接線方向の接触剛性(Kt)の比のことです(接触剛性(K)は[高度]ボタンで設定します。)「サーフェス間接触の高度なコントロール」のページを参照してください)。 接線方向の剛性が大きいほど、結果の精度が向上しますが、その代償として、より多くの反復が必要になります。 接線方向の剛性が小さいほど、収束性に優れます(実行時間が短縮されます)が、精度が低下する可能性をともないます。推奨される値は、0.01 ~ 1 の範囲で、既定は 0.01 です。静摩擦係数を大きくするほど、接線方向の剛性比を小さくすることをお勧めします。
|
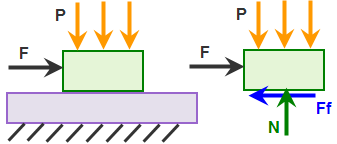
(a) トップ ブロックのモデルと自由物体図(Free body diagram)。加えられた力 F は、静摩擦力を超えるまで、時間とともに徐々に増加します。 |
|
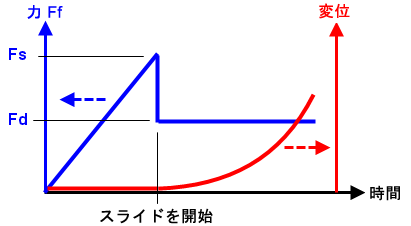
(b) 摩擦力 Ff の時間変化(青色の曲線)と変位の時間変化(赤色の曲線)。 摩擦力 Ff が静摩擦の限界(Fs = μs * N)を超えるまで、パーツの運動はありません。静摩擦を超えると、摩擦力 Ff は Fs から Fd (= μd * N) にまで低下し、パーツは加速を開始します。 |
|
(c) (b)のグラフは摩擦力と変位の関係を示すように組み合わされています。理想状態では、摩擦力が Fs に達するまで変位はゼロであり、その後にすべりが開始します。数値上でこれを実現するのは困難です。変位がゼロでない場合はすべて摩擦力が Fd であること意味するためです。 |
|
(d) (c)における数値的な不安定さを回避するために、摩擦力が静的限界(Fs)未満のときに、パーツが少し(Δs)だけ変位できるようになっています。運動の大きさは、接線方向の剛性(Kt = Fs/Δs)によってコントロールされます。Kt の値が小さいほど、パーツはすべりを開始する前に大きく変位することがで、収束が容易になります。一方、Kt の値が大きい(勾配が急である)ほど、すべりを開始する前の変位は小さくなり、収束が困難になります。 接線方向の剛性は、(接線方向の剛性比) x (垂線方向の剛性)によって計算されます。 |
| 図 3: 修正クーロン摩擦に対する接線方向の剛性 |
粘性摩擦のあるクーロン
修正されたクーロン摩擦則とは異なり、静摩擦および動摩擦の摩擦係数はともに粘性摩擦のあるクーロンを考慮しません。修正されたクーロン摩擦則では、静摩擦および開始モーションを解決するために、比較的高い力が必要です。スライドを開始すると、スライド摩擦係数が静止係数より小さくなっているため、摩擦力が 減少 します。したがって、摩擦力の急激な変化により、力の不連続が発生します。粘性摩擦のあるクーロン則では、スライドが始まっても、摩擦力の不連続は発生しません。代わりに、スライドの速度が高まると、摩擦力が徐々に 増加 します。
[粘性摩擦のあるクーロン]オプションでは、2 つのパラメータを定義する必要があります。
- スライド摩擦係数(Fd): これは動摩擦係数とも呼ばれます。接触パーツ間の相対モーションと垂直力を維持するために必要な接線力の比率です。たとえば、1 つのブロックを隣接するパーツに沿ってスライドを続けさせるために 15N の接線力が必要で、それらの間の法線接触力が 100N である場合、この場合のスライド摩擦係数は 15N / 100N = 0.15 となります。この摩擦則の目的は、スライド摩擦係数を相対的な低速度のスライドをベースにすることです。
- 粘性摩擦係数(νf): これは、摩擦力対スライド速度の曲線の勾配です。すべての粘性効果で同様ですが、粘性効果を克服するために必要な力は、速度に比例します。
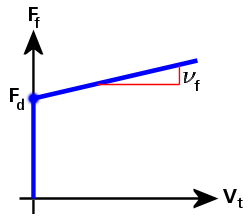
図 4: 摩擦力対スライド速度(粘性摩擦のあるクーロン)
図 4 における摩擦力(Ff)曲線は次のように定義されます。
Ff = Fd + νf · Vt
ここで
Fd は動(スライド)摩擦力、
νf は粘性摩擦係数、
Vt は、2 つのパーツ間の接線(スライド)速度です。
νf = 0 の場合は、Ff = Fd です。
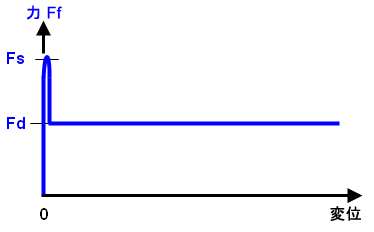
クーロン摩擦を平滑化
粘性摩擦のあるクーロン則と同様に、クーロン摩擦を平滑化則もスライド摩擦係数のみを考慮します。これよにり、修正されたクーロン摩擦則を使用した場合に発生する静止状態とスライド状態の摩擦力の連続性が中断されます。静止状態とスライド状態間の遷移が、よりスムーズな遷移係数(Φ)の包含によって安定化されます。
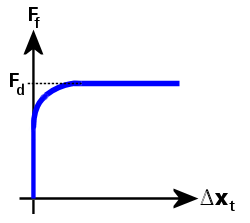
図 5: 摩擦力対接線相対変位(クーロン摩擦を平滑化)
図 5 で、摩擦力(Ff)曲線は次のように定義されます。
Ff = Fd · Φ、および
Φ = tanh(3 · Δxt / δ)
ここで
Fd は動(スライド)摩擦力です。
Φ は遷移係数であり、接線の相対変位がゼロに近づくにつれて摩擦力をスムーズにゼロへアプローチさせることができます。同様に、接線の相対変位が増えるにつれて摩擦力をスムーズに動摩擦力へアプローチさせることができます。
Δxt は接線の相対変位であり、
δ は接触剛性および動的摩擦力に基づいて計算される許容値です。