유도 가열의 전자기 현상은 맥스웰 방정식에 의해 수학적으로 설명됩니다.
미분 형식의 맥스웰 방정식은 다음과 같이 작성할 수 있습니다.
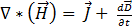 (암페어 법칙)[1]
(암페어 법칙)[1]
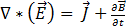 (패러데이 법칙)[2]
(패러데이 법칙)[2]
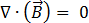 (가우스 법칙)[3]
(가우스 법칙)[3]
 (가우스 법칙)[4]
(가우스 법칙)[4]
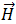 : 자기장 밀도,
: 자기장 밀도, 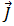 : 유도 전류 밀도,
: 유도 전류 밀도, 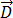 : 전기 플럭스 밀도,
: 전기 플럭스 밀도, 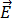 : 전기장,
: 전기장, 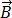 : 자속 밀도,
: 자속 밀도, 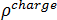 : 전기 충전 밀도 및
: 전기 충전 밀도 및 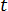 : 시간.
: 시간.
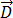 및
및 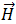 는 다음 방정식에 따라 유전율
는 다음 방정식에 따라 유전율  및 자기 투과율
및 자기 투과율 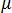 의 전자기 재료 속성을 통해
의 전자기 재료 속성을 통해 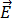 및
및 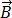 에 관련될 수 있습니다.
에 관련될 수 있습니다.
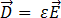 [5]
[5]
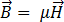 [6]
[6]
옴 법칙을 사용하여 맥스웰 방정식을 더욱 줄일 수 있습니다.
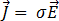 [7]
[7]
방정식 [5]와 [7]을 방정식 [1]에 대체할 경우 10mHz 미만의 전기 주파수에서 유도 전류 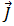 가 변위된 전류 밀도
가 변위된 전류 밀도 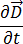 보다 크기 때문에 이 항을 무시할 수 있으므로 방정식 [1]을 다음과 같이 작성할 수 있습니다.
보다 크기 때문에 이 항을 무시할 수 있으므로 방정식 [1]을 다음과 같이 작성할 수 있습니다.
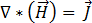 [8]
[8]
자속 밀도 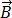 가 방정식 [3]의 0 발산을 충족하기 때문에 다음과 같이 자기 벡터 포텐셜
가 방정식 [3]의 0 발산을 충족하기 때문에 다음과 같이 자기 벡터 포텐셜 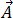 로 표시할 수 있습니다.
로 표시할 수 있습니다.
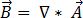 [9]
[9]
방정식 [9]를 방정식 [2]에 대체하면 다음과 같이 됩니다.
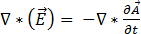 [10]
[10]
따라서 다음과 같습니다.
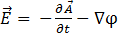 [11]
[11]
여기서 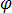 는 전기 스칼라 포텐셜입니다. 이제 방정식 [7]은 다음과 같이 됩니다.
는 전기 스칼라 포텐셜입니다. 이제 방정식 [7]은 다음과 같이 됩니다.
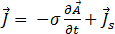 [12]
[12]
여기서 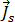 는 코일의 소스 전류 밀도 진폭이며 다음에 의해 제공됩니다.
는 코일의 소스 전류 밀도 진폭이며 다음에 의해 제공됩니다.
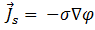 [13]
[13]
방정식 [6], [9] 및 [12]를 방정식 [8]에 대체하면 다음과 같이 됩니다.
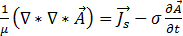 [14]
[14]
이제 방정식 [14]에 삼중적 벡터 ID 방정식 [15]를 사용합니다.
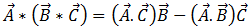 [15]
[15]
그러면 다음과 같이 됩니다.
 [16]
[16]
이제 하나의 구성요소 벡터 포텐셜 장에 대해 다음과 같습니다.
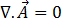 [17]
[17]
이 경우 방정식 [16]은 다음과 같이 정리됩니다.
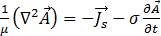 [18]
[18]
사인 안정 상태 각주파수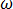 = 2
= 2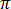 f이고 단위가 (rad/s)인 사인곡선적 안정 상태에서 방정식 [18]은 다음과 같이 됩니다.
f이고 단위가 (rad/s)인 사인곡선적 안정 상태에서 방정식 [18]은 다음과 같이 됩니다.
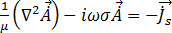 [19]
[19]
시간 고조파 자기 벡터 포텐셜 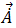 이 해결되면 방정식 [9]에서 자기장 플럭스 밀도를 구할 수 있습니다. 도체의 시간 고조파 유도 와전류
이 해결되면 방정식 [9]에서 자기장 플럭스 밀도를 구할 수 있습니다. 도체의 시간 고조파 유도 와전류 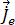 는 방정식 [20]에 의해 제공됩니다.
는 방정식 [20]에 의해 제공됩니다.
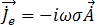 [20]
[20]
여기서 도체의 줄 열 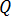 을 구할 수 있습니다.
을 구할 수 있습니다.
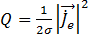 [21]
[21]
줄 열은 도체의 와전류에 의해 유도된 체적 열 소스이며 단위는 (W/m3)입니다.
유도 가열에서 발생하는 열전달 현상은 도체 내의 열 전도이며 모든 시뮬레이션에서 사용되는 천이 열 전도 방정식으로 설명됩니다.
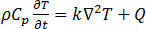 [22]
[22]
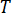 : 온도,
: 온도, 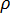 : 밀도,
: 밀도, 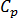 : 비열 용량,
: 비열 용량, 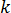 : 재료의 열전도 계수 및
: 재료의 열전도 계수 및 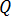 : 방정식 [21]의 줄 열.
: 방정식 [21]의 줄 열.