잔류 응력 수축 예측 모델은 선형 열점탄성 재료 동작을 가정하여 공식화되었습니다. 이 모델은 재료가 금형의 압력을 받아 냉각되는 동안 생긴 응력을 고려합니다. 이 방법에서는 수축 변형을 계산하는 대신 각 요소에 대한 잔류 응력 분포를 직접 계산합니다.
잔류 응력 분포는 유동에 평행 및 수직인 방향으로 각 요소의 두께에 응력을 제공합니다. 이 응력 분포는 응력 해석 프로그램의 입력이 되어 제품의 변형된 형상을 얻습니다. 또한 재료에 실험 수축 데이터를 사용할 수 있는 경우 잔류 변형 방법을 사용할 때보다 더 정확하게 수축을 예측하므로 제품 변형을 얻을 수 있습니다.
방법에 대한 일반적인 설명
모델은 선형 열점탄성 재료 동작을 가정하여 공식화되었습니다. 이 모델은 재료가 금형의 압력을 받아 냉각되는 동안 생긴 응력을 고려합니다. 특히 이 모델은 압력 유도 응력뿐만 아니라 재료의 고화 및 후속 수축으로 발생되는 열 유도 응력을 고려합니다. 압력 유도 응력은 고화층을 형성하는 고화된 재료에서 용융 압력의 동작에 의해 발생됩니다. 이론상 이 모델은 재료에 수축 데이터를 사용할 수 없는 경우에도 사용할 수 있다는 이점이 있습니다. 그러나 수축 데이터를 사용할 수 있는 경우 성능이 현저하게 향상됩니다.
수축 및 변형 예측은 계산된 열 및 압력 유도 잔류 응력 분포를 기반으로 합니다. 현재 개발의 계산 절차는 아래에 나열되어 있으며, 섬유 충전 재료에 대한 절차입니다. 충전되지 않은 재료의 경우 절차는 비슷하지만 기계적 속성 계산이 필요하지 않습니다.
각 시간 단계의 경우:
- 유체 역학 계산:
- 압력 p, 유량 Q...
- 섬유 배향
- 열전달 계산:
- 온도 T
- 고화층
- 열역학 계산:
- f (p, v, T)=0
- 점도 업데이트
- 솔루션이 수렴됩니까?
- 아니오일 경우 1단계를 반복하십시오.
- 예일 경우 6단계로 이동하십시오.
- 마이크로공학 계산:
-
열기계 속성:
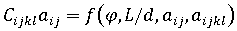
-
- 열점탄성 계산:
- 열 및 압력 유도 응력
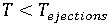 일 경우 다음 시간 단계로 이동하십시오(1단계에서 반복).
일 경우 다음 시간 단계로 이동하십시오(1단계에서 반복).
참고: 잔류 열 응력 수축 모델을 선택하면 변형 해석에서 비대칭 충전+보압 해석에 의해 생성된 비대칭 정보를 사용합니다. 이 비대칭은 금형의 두 면 간 온도 차이 또는/및 분기 지오메트리에 의해 발생될 수 있습니다. 따라서 냉각 해석 결과가 없는 경우에도 제품에 분기 지오메트리가 있으면 변형 결과에 몇 가지 비대칭 효과가 표시될 수 있습니다. 그러나 충전+보압 해석이 대칭이면 변형 해석이 대칭이 되므로 냉각 효과를 무시합니다.
수축 데이터를 사용할 수 없는 때 이 방법 적용
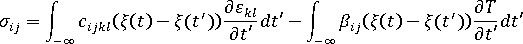
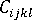 그리고
그리고 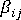 는 각각 재료의 기계 및 열 특성을 정의하는 텐서입니다.
는 각각 재료의 기계 및 열 특성을 정의하는 텐서입니다. 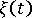 는 재료의 온도 종속성을 고려하는 유사 시간 배율이며 다음 방정식으로 정의됩니다. 여기서
는 재료의 온도 종속성을 고려하는 유사 시간 배율이며 다음 방정식으로 정의됩니다. 여기서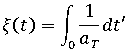
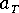 는 재료 및 온도 범위에 따라 WLF 방정식이나 아레니우스 방정식으로 특징지어진 시간-온도 시프트 계수입니다.
는 재료 및 온도 범위에 따라 WLF 방정식이나 아레니우스 방정식으로 특징지어진 시간-온도 시프트 계수입니다.
- 비섬유 충전 재료의 경우 모델이 등방성이어서 기계 속성 텐서
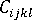 이 Autodesk Moldflow 재료 데이터베이스에 저장된 재료의 계수 및 푸아송 비에 따라 정의되고 열 속성 텐서
이 Autodesk Moldflow 재료 데이터베이스에 저장된 재료의 계수 및 푸아송 비에 따라 정의되고 열 속성 텐서 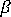 를 정의하는 데 사용된 열 팽창 계수는 재료에 대한 pvT 데이터에서 얻습니다.
를 정의하는 데 사용된 열 팽창 계수는 재료에 대한 pvT 데이터에서 얻습니다. - 섬유 충전 재료의 경우 이러한 텐서가 컴포지트 재료에 대한 이방성 기계 및 열 속성을 사용하여 정의되며, 충전+보압 해석에서 얻은 섬유 배향 분포에서 계산됩니다. 이 경우 모델은 섬유 배향 방향을 따라 횡적으로 응력을 예측합니다.
- 재료가 천이 온도보다 낮아질 때까지 재료에 응력이 생성되지 않습니다.
- x3 방향이 지역 미드플레인에 대한 법선인 지역 요소 좌표를 기준으로 할 때 전단 응력 =
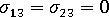 입니다.
입니다. - 법선 응력
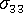 은 두께 전체에서 일정합니다.
은 두께 전체에서 일정합니다. -
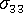 < 0인 한 재료가 금형 벽에 부착됩니다.
< 0인 한 재료가 금형 벽에 부착됩니다. - 재료가 금형에 있는 한 구속된 급랭 조건이 모든 사례에서 규정됩니다.
- 금형 탄성이 무시됩니다. 금형 코어의 탄성이 코어 시프트 해석에서 고려됩니다.
- 제품이 취출된 후 재료가 탄성 솔리드처럼 동작합니다.
이 모델은 수축 특성화를 수행했는지 여부에 관계없이 Autodesk Moldflow 재료 데이터베이스의 모든 재료에 사용할 수 있습니다. 섬유 충전 재료의 경우 모델을 사용하려면 공정 설정 마법사-충전+보압 설정 대화상자에서 섬유 재료인 경우 섬유 배향 해석을 수행하는 옵션을 선택해야 합니다.
이 모델은 수축 추세를 예측할 수 있지만 절대값과 관련하여 본질적인 오류가 있을 수 있습니다. 이 모델은 변형을 줄이기 위한 설계에 유용하지만 수축 데이터를 사용할 수 있을 때보다 절대값이 덜 정확합니다. 충전되지 않은 재료의 경우 유동 해석 소프트웨어에서 분자 배향 또는 결정화도의 효과를 계산하는 기능이 없으므로 모델이 등방성입니다.
수축 데이터를 사용할 수 있을 때 이 방법 적용
- 현재 측정 방법을 사용하여 실제 사출 성형 조건에서 동작을 나타낼 수 없는 pvT 데이터 및 천이 온도에서 수축의 종속성이 민감합니다.
- 분자 배향을 결정하는 규정이 없으므로 충전되지 않은 재료의 경우 모델에서 이방성을 예측하지 못합니다.
- 결정화도 효과에 대한 규정이 부족합니다.
- 점탄성 계산을 위한 이완 스펙트럼 데이터가 부족합니다.
재료가 Autodesk Moldflow에서 수축 특성화된 경우 측정된 수축 결과를 고려하여 열점탄성 모델을 현저하게 향상시킬 수 있습니다. 이 작업은 측정된 수축과 예측된 수축 사이의 차이를 줄이기 위해 측정된 수축 데이터와 관련된 하이브리드 모델의 독립 변수 중 하나로 이론 모델을 사용하여 수행합니다. 결과 모델을 수정된 잔류 인-몰드 응력(CRIMS: Corrected Residual In-Mold Stress) 모델이라고 합니다.
이 아이디어는 아래 그림과 같이 표시됩니다.
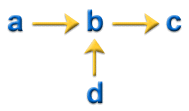
수정된 잔류 인-몰드 응력(CRIMS: Corrected Residual In-Mold Stress) 모델
. (a) 예측된 등방성 잔류 응력 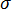 , (b) 오류 수정, (c) 수정된 이방성 잔류 응력
, (b) 오류 수정, (c) 수정된 이방성 잔류 응력 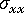 그리고
그리고  , (d) 측정된 수축.
, (d) 측정된 수축.
이 효과를 설명하려면 다음 그래프를 참조하십시오.
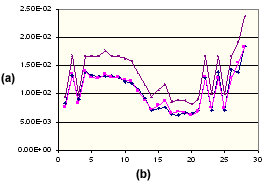
폴리프로필렌의 평행 수축
. (a) 수축 %, (b) 성형 조건 세트 번호, ![]() 측정된 평행,
측정된 평행, ![]() 수정된 평행,
수정된 평행, ![]() 계산된 중요(등방성).
계산된 중요(등방성).
다음 그래프는 폴리프로필렌의 유동 방향에 대해 평행으로 측정된 실험 수축을 보여줍니다. 또한 열점탄성 모델을 사용하여 이론적으로 계산된 평행 수축 값 및 수정된 평행 수축 값도 보여줍니다. 수정된 값이 측정된 값과 정확히 일치하는 것을 확인할 수 있습니다. 아래 표시된 대로 동일한 폴리프로필렌의 수직 방향도 유사하게 개선된 것을 확인할 수 있습니다.
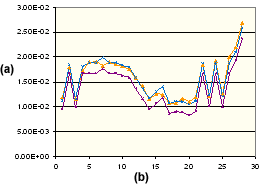
폴리프로필렌의 수직 수축
. (a) 수축 %, (b) 성형 조건 세트 번호, ![]() 측정된 수직,
측정된 수직, ![]() 수정된 수직,
수정된 수직, ![]() 계산된 중요(등방성).
계산된 중요(등방성).
수정 개념은 섬유 충전 재료에도 적용할 수 있으며 뛰어난 결과를 제공합니다. 다음은 중량이 유리섬유 보강재의 15%인 PA66에 대한 몇 가지 결과입니다.
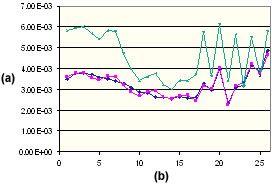
PA66 15% GF의 평행 수축
. (a) 수축 %, (b) 성형 조건 세트 번호, ![]() 측정된 평행,
측정된 평행, ![]() 수정된 평행,
수정된 평행, ![]() 이론적 평행.
이론적 평행.
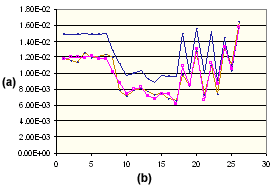
PA66 15% GF의 수직 수축
. (a) 수축 %, (b) 성형 조건 세트 번호, ![]() 측정된 수직,
측정된 수직, ![]() 이론적 수직,
이론적 수직, ![]() 수정된 수직
수정된 수직
단일 변량 해석에 사용되었을 때 이 방법 적용
단일 변량 해석은 Autodesk Moldflow 변형 해석 제품에서 변형의 주요 원인을 분리하기 위해 제공되는 기술로, 대상 측정을 사용하여 제품 변형을 줄일 수 있도록 합니다. 이 기술은 단일 변량 해석 항목에서 자세히 설명합니다. 여기서는 단일 변량 해석 컨텍스트에서 잔류 응력 방법이 적용되는 방식을 살펴봅니다.
충전 및 보압 단계의 충전+보압 해석은 잔류 응력 계산에서 입력으로 사용되는 다음과 같은 정보를 출력합니다.
- 일반화된 힘 데이터, 즉 지역 요소 축 시스템의 각 요소에 대한 멤브레인 힘(
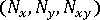 ) 및 벤딩 모멘트(
) 및 벤딩 모멘트(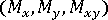 )
) - 각 요소에 대한 재료 배향 각도
- 각 요소에 대한 기계 속성(세로 탄성계수, 가로 탄성계수 및 푸아송 비)
단일 변량 해석은 변형의 원인이 다음 세 범주에 해당한다는 개념을 기반으로 합니다.
- 냉각 효과
- 수축 효과
- 배향 효과
이 개념은 응력이 아닌 수축과 관련이 있습니다. 따라서 잔류 응력 모델을 사용할 때 위의 세 가지 효과 측면에서 변형의 원인을 분리하려면 지정된 일반화된 힘에서 일반화된 변형을 계산한 다음 냉각 효과, 수축 효과 및 배향 효과로 인해 변형을 성분으로 해석하고 마지막으로 수정된 변형을 해당 일반화된 힘으로 다시 변환해야 합니다. 그런 다음 별도의 응력 해석을 수행하여 각 효과에 대한 변형 결과를 얻습니다. 계산과 관련된 방정식은 아래에 요약되어 있습니다.
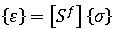
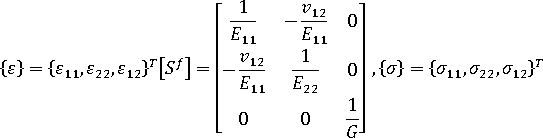
또는 훅의 법칙은 강성 매트릭스 측면에서 다음과 같이 기록할 수 있습니다.
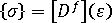
그리고
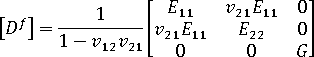
재료 배향 각도 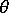 이(가) 지정된 경우 컴플라이언스 매트릭스 및 강성 매트릭스를 배향된 시스템에서 지역 요소 시스템으로 변환합니다.
이(가) 지정된 경우 컴플라이언스 매트릭스 및 강성 매트릭스를 배향된 시스템에서 지역 요소 시스템으로 변환합니다.
일반화된 변형이 다음과 같이 지정됨
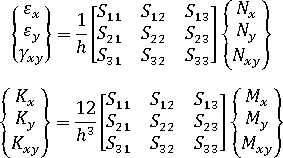
여기서 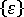 는 및
는 및 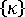 는 각각 변형 및 곡률 벡터입니다.
는 각각 변형 및 곡률 벡터입니다.
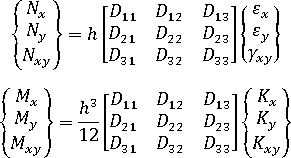
변형의 효과를 분리하기 위해 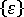 및
및 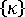 를 해석된 성분으로 바꾼 다음 멤브레인 힘과 벤딩 모멘트를 다시 계산하고 구조 해석에서 새 값을 사용합니다.
를 해석된 성분으로 바꾼 다음 멤브레인 힘과 벤딩 모멘트를 다시 계산하고 구조 해석에서 새 값을 사용합니다.