긴 섬유 컴포지트에 대한 섬유 절단 모델

긴 섬유 컴포지트 재료를 사용하여 섬유 배향 해석을 수행할 때 섬유 절단을 계산하는 옵션이 구현되었습니다.

구현된 섬유 절단 모델은 유동 필드에서 좌굴 및 전단력으로 인한 섬유 절단 확률을 설명하는 통계 모델로 Phelps 및 Tucker[1]가 처음 제안했습니다.

단일 섬유의 경우 유체 역학 힘에 의한 절단 확률은 다음과 같이 표현할 수 있습니다.

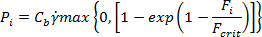
여기서 힘 비율은 Dinh 및 Armstrong[2]이 설명한 유체 역학 압축력 대 중요 좌굴 힘으로, 다음과 같습니다.

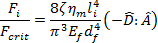
여기에서 각 항목은 다음과 같습니다. 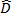및 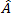는 각각 변형률 텐서 및 섬유 배향 텐서입니다. 다른 변수는 드래그 계수인 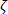을 제외하고 섬유 및 매트릭스의 속성입니다.

절단 여부에 관계없이 섬유는 유동 필드에서 사라지거나 증가할 수 없기 때문에 보존 법칙을 따라야 합니다. 이 보존 법칙은 다음과 같이 표현할 수 있습니다.

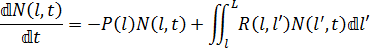
여기서 L은 초기 섬유 길이이고, N(l,t)는 t 시간에 길이가 l인 섬유 수, P(l)는 섬유 길이 l의 스칼라 확률 함수, R(l,l')는 절단되어 길이가 l'인 섬유를 형성하는 섬유 길이 l의 확률 함수(여기서 l'<l)입니다. 다음과 같이 가우스 절단 프로파일로 표현할 수 있습니다.

여기에서 각 항목은 다음과 같습니다. 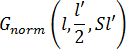는 평균이 l'/2이고 표준 편차가 Sl'인 변수 l에 대한 가우스 법선 확률 밀도 함수입니다. S는 가우스 절단 프로파일의 형상을 제어하는 데 사용할 수 있는 무차원 피팅 변수입니다.

참조 문헌

1. Phelps, J.H., Processing-microstructure Models for Short- and Long-fiber Thermoplastic Composites. Ph.D. thesis, University of Illinois at Urbana-Champaign (2009).
2. Dinh, S.M. and Armstrong, R.C., A Rheological Equation of State for Semi-Concentrated Fiber Suspensions. J. Rheol., 28(3):207-227 (1984).