Os fenómenos eletromagnéticos do aquecimento por indução são descritos matematicamente pelas equações Maxwell.
As equações Maxwell, em formato diferencial, podem ser escritas como:
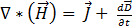(a partir da lei de Ampere) [1]
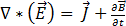(a partir da lei de Faraday) [2]
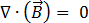(a partir da lei de Gauss) [3]
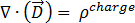(a partir da lei de Gauss) [4]
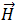é a intensidade do campo magnético, 
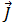é a densidade da corrente de condução, 
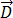é a densidade do fluxo elétrico, 
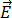é o campo elétrico, 
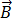é a densidade do fluxo magnético, 
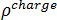é a densidade da carga elétrica e 
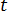é o período de tempo.
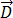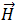e podem estar relacionados com 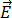e 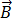através das propriedades de constante dielétrica do material eletromagnético, de 
e da permeabilidade magnética, e de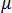 
de acordo com as seguintes equações:
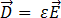[5]
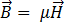[6]
As equações Maxwell podem ser ainda mais reduzidas através da utilização da lei de Ohm:
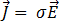[7]
Substituindo as equações [5] e [7] pela equação [1], e sabendo que, para as frequências de corrente menores que 10 MHz, a corrente induzida, 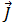, é maior que a densidade da corrente de deslocamento, 
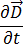, permitindo ignorar este termo, então a equação [1] pode ser escrita:
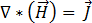[8]
Como a densidade do fluxo magnético, 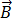, cumpre a divergência zero da equação [3], pode ser expressa como um potencial do vetor magnético, 
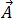, para que:
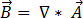[9]
Substituindo a equação [9] pela equação [2] resulta em:
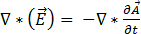[10]
Assim,
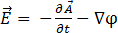[11]
em que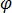 
é o potencial de escala elétrico. A equação [7] torna-se:
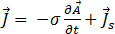[12]
em que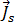 
é a amplitude da densidade da corrente de origem na bobina, sendo especificada por:
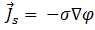[13]
Substituindo as equações [6], [9] e [12] pela equação [8] resulta em:
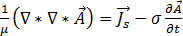[14]
Agora, a utilização da equação de identidade de produto de vetor triplo 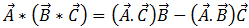[15]
[15]
na equação [14] resulta em:
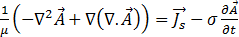[16]
Agora, sabendo que para os campos de potencial de vetor de uma componente
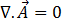[17]
a equação [16] é então reduzida para
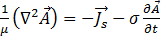[18]
Para o estado sinusoidal estacionário com a frequência angular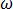 
= 2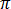
f, e as unidades (rad/s), a equação [18] torna-se:
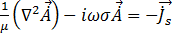[19]
Assim que o potencial de vetor magnético harmónico,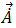 
, for resolvido, será possível calcular a densidade do fluxo do campo magnético através da equação [9]. As correntes Eddy induzidas pela harmónica de tempo, 
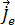, nos condutores é calculada pela equação 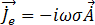[20]:
[20]
A partir da qual é possível calcular o aquecimento de Joule,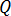 
, nos condutores:
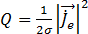[21]
O aquecimento de Joule é a fonte de calor volumétrico, com as unidades (W/m3), que é induzida pelas correntes Eddy no condutor.
O fenómeno de transferência de calor ocorrido no aquecimento por indução corresponde à condução de calor no condutor, sendo descrito pela equação de condução de calor transiente utilizada em todas as simulações.
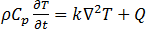[22]
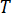é a temperatura, 
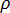é a densidade, 
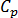é a capacidade de calor específico, 
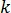é a condutividade térmica do material e 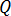- é o aquecimento de Joule calculado pela equação [21].