Выпадающий список содержит следующие типы геометрии плиты и ее параметры:
|
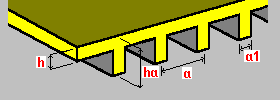
Односторонние ребра одного направления: h — толщина плиты ha - высота ребра a - шаг ребер a1 - ширина ребер |
|
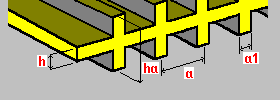
Двусторонние ребра одного направления: h — толщина плиты ha - высота ребра a - шаг ребер a1 - ширина ребер |
|
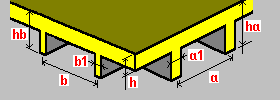
Односторонние двунаправленные ребра: h — толщина плиты ha - высота ребра hb - высота ребра a - шаг ребер a1 - ширина ребра b - шаг ребер b — ширина ребра |
|
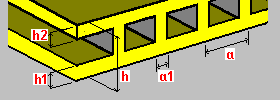
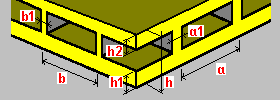
Однонаправленный коробчатый пол: h — толщина перекрытия h1 - толщина нижней плиты h2 - толщина верхней плиты a - шаг ребер a1 - ширина ребер |
|
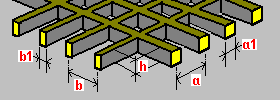
Двунаправленный коробчатый пол: h — толщина перекрытия h1 - толщина нижней плиты h2 - толщина верхней плиты a - шаг ребер a1 - ширина ребра b - шаг ребер b1 - ширина ребер |
|
Балочная клетка: h - высота ребра a - шаг ребер a1 - ширина ребра b - шаг ребер b1 - ширина ребер |
|
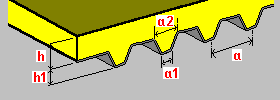
Плита на профнастиле: h — толщина плиты h1 – высота плиты a – шаг ребер a1 – ширина ребра у основания a2 – ширина волны профнастила в широкой части. |
|
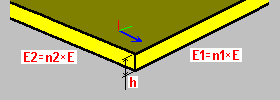
Ортотропный материал: h — толщина плиты n1 - коэффициент податливости n2 - коэффициент податливости |
|
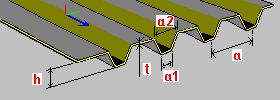
Gрофнастил: h — высота плиты t — толщина плиты a, a1, a2 – размеры сегмента одиночной плиты/волны профнастила (шаг, ширина) |
|
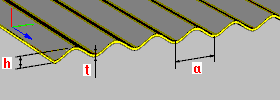
Волнистая плита (волнистый профнастил): h — высота плиты t — толщина плиты a1 — толщина ребра |
|
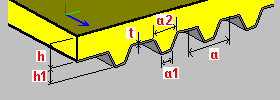
Перекрытие из трапецеидальной плиты h - толщина плиты h1 - высота профнастила t — толщина плиты a, a1, a2 - размеры единичного сегмента (расстановка, ширина) Es - Модуль Юнга (для стали трапеции) vs - Коэффициент Пуассона (для стали трапеции) Eb - Модуль Юнга (для бетона; значение принимается на основе выбранного материала) vb — Коэффициент Пуассона (для бетона; значение принимается на основе выбранного материала) |
|
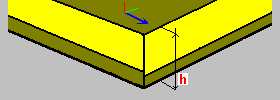
Постоянная толщина с приведенной жесткостью: h - толщина плиты Переводные коэффициенты матрицы элементов: мембранная жесткость D, жесткость на изгиб K и жесткость на поперечную силу H; кроме того, можно определить коэффициент уменьшения веса учитываются во время формирования из нагрузки от собственного веса; значения этих коэффициенты определяются в коэффициенты жесткость, вес, диалоговое окно, которое открывается после нажатия кнопки Коэффициенты. |

|
Пустотелая плита (с круглыми или овальными проемами) h - толщина плиты a - расстояния между ребрами, интервалы a1 - ширина проема / диаметр отверстия ho - высота отверстиия (плита с овальными отверстиями) hc - расстояние между центром отверстия и краем плиты h1 - высота нижней кромки перекрытия h2 — высота верхней кромки плиты (h2 = h - hc - c/2 - a1/2) c = ho - a1 (для перекрытия с овальными отверстиями) Опция Игнорировать поперечную изгибную жесткость позволяет опустить или рассматривать при изгибе жесткость K_YYYY в вычислениях. Игнорирование поперечной изгибной жесткости (в направлении Y) позволяют лучше моделировать работу сборных пустотных железобетонных плит. |
Ортотропный материал порождает различную жесткость плиты в перпендикулярных направлениях из-за различных физических свойств. Различие в жесткости вызывается различными модулями Юнга E1 и E2, соответственно, в направлениях ортотропии x, y. Модули E1, E2 вместе с коэффициентами n1, n2 задаются пользователем. Коэффициент Пуассона для обоих направлений сохраняется равным исходному. Такой тип ортотропии может быть полезным, например, в моделировании плит с усилениями в обоих направлениях.
Жесткость таких плит в обоих направлениях может быть вычислена на основе приведенной ниже формулы. Предположим, что материал линейно упругий, тогда коэффициент упругости для направления, параллельного направлению усиления, равен:
n = 1+ 12/(h*h) * e*e * m * u / (1+ m*u)
где
h – высота сечения плиты
m = Ez/Eb – отношение модулей Юнга стали и бетона.
e – расстояние между центром тяжести усилений и срединной плоскостью плиты
u — усиление (выраженное десятичной дробью), т. е. площадь сечения усиливающего стержня, отнесенная к соответствующей части сечения плиты.
См. также: