Теоретическая база методов динамического расчета конструкций

Введение

Этот документ содержит описание методов динамического расчета, которые применяются в Robot. В приложениях приведены подробности по теоретическим основам и примеры. Данный раздел не является руководством пользователя и не ставит целью ознакомить пользователя с деталями интерфейса программы Robot. Его целью является только объяснить основные идеи, которые реализованы в этой программе.

Большинство динамических методов в Robot основано на использовании результатов модального расчета. Необходимо иметь в виду, что методы модального расчета зависят от типа выбранного решателя. Прямой решатель систем с матрицами профильного хранения используется для реализации следующих методов: метода блочных итераций в подпространствах (BLSI), метода итераций в подпространствах (SI), метода Ланцоша и основного метода редукции. Прямой решатель систем с разреженными матрицами применяется при использовании метода блочных итераций в подпространствах(BLSI), метода Ланцоша и основного метода редукции. В то время, как для итерационного решателя доступны следующие методы: модифицированный метод Ланцоша (метод псевдомод – см. п. 3.5 и приложения 3А, 3В), градиентный метод Ритца (PCG_Ritz) и метод сопряженных градиентов с предобусловливателем (PCG).

Прямой решатель для разреженных матриц (SPDS) – это особая форма метода исключения по Гауссу. Он настоятельно рекомендуется для расчета пространственных конструкций и решения задач высокого порядка (10 000 – 200 000 уравнений) и является хорошей альтернативой итерационному решению.

3.1. Методы определения собственных форм

Модальный расчет включает два основных подхода. Расчет собственных значений

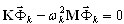k = 1; 2; ..., N (3.1)

проводится путем определения собственных значений wk и собственных векторов 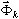. Этот первый подход инженерам знаком. Второй подход состоит в построении базисных векторос

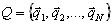(3.2)

и поиске апроксимаций по Ритцу , (k=1; 2; ..., N). Он основан на идее, аналогичной методу "Векторов Ритца, зависящих от нагрузки", предложенной в работах - E.L. Wilson [1, 3] и реализованной в SAP2000. Этот подход был применен к решению сейсмической задачи и является мощным средством в случае, когда существуют большие трудности с получением удовлетворительного вклада масс (см. раздел 3.5).

Если выбран прямой решатель (решатель систем с матрицами профильного хранения или SPDS), то могут использоваться следующие методы: блочных итераций в подпространствах (BLSI), итераций в подпространствах (SI), ортогонализации Ланцоша и основной метод редукции (см. приложение 3А). Метод итерации в подпространствах обычно медленный. Поэтому при решении пространственных и задач высокого порядка, когда требуется определить большое число собственных чисел и собственных векторов рекомендуется использовать метод (BLSI) или метод Ланцоша. Метод основной редукции может быть эффективно использован инженерами-экспериментаторами, однако он требует достаточной информации о базисных узлах и соответствующих базисных направлениях.

Метод сопряженных градиентов с предобусловливателем (PCG)

Этот метод используется при решении первой задачи, когда выбран итерационное решение. Такой подход может быть очень эффективным, когда задача собственных значений имеет невысокий порядок (не выше 5). Этот метод имеет смысл использовать скорее при расчете на ветровые нагрузки, нежели при сейсмическом расчете. Метод PCG можно использовать и для оценки первой собственной частоты в задаче высокого порядка.

Второй подход (который реализуется методом Псевдомод) представлен в разделе 3.5.

Метод блочных итераций в подпространствах (BLSI)

Этотм метод [1; 3] является более общим по сравнению с методом Ланцоша, поскольку он допускает любые типы матриц масс (см. раздел 3.2) и пригоден для расчета отдельных конструкций. Более быстрые вычисления по сравнению с обычным итерационным методом в подпространствах [1-3] обеспечивают итерации в блоке постоянного размера с немедленным исключением сходящихся векторов, за которым следует новый старт. Как и метод Ланцоша, метод BLSI может использоваться для решения задачи собственных значений высокого порядка (до 100 – 200).

Метод итераций в подпространствах (SI)

Этот метод может использоваться для расчета всех типов матриц масс [4] и для расчета отдельных конструкций, однако при необходимости определения большого числа мод - примерно N > 10 этот метод требует большой затраты времени, особенно при решении задач высокого порядка.

Метод Ланцоша [12; 16; 17] – очень эффективный метод, позволяющий получить большое число собственных значений (N ~ 20 – 500 и более). Хотя метод предпочтителен при решении задач высокого порядка, его использование имеет ряд ограничений:

• метод не пригоден при расчете отдельных конструкций;
• матрица масс должна быть "сосредоточенная с вращениями" или "совместимая";
• нельзя пренебрегать плотностью материала (чтобы обойти это ограничение, достаточно ввести малую фиктивную плотность).

Основной метод редукции

Этот метод [5] известен как усовершенствованный метод Релея-Ритца [4] или как метод Бубнова-Галеркина для дискретных систем. Этот алгоритм используется для получения приближенных значений для нескольких первых собственных пар, если имеется какая-либо информация о них. Для получения редуцированной системы метод требует задания основных степеней свободы (MDOF). То есть, можно контролировать процесс создания редуцированной модели. Это является мощным средством для того, кто имеет опыт динамического расчета конструкций и рассчитывает конструкцию такого типа, свойства которого уже известны. Этот метод позволяет исключить ненужные степени свободы (DOF) из редуцированной модели и преобразовать первоначально сложную исходную задачу с большим числом степеней свободы к редуцированному виду со сравнительно малым числом степеней свободы Это достигается со значительно меньшим числом степеней свободы. Опыт проведения динамического расчета показывает, что этим методом можно решить некоторые задачи, которые при использовании автоматических методов редукции (методов BLSI, SI и метод Ланцоша) требуют очень сложных вычислительных процессов. Например, отыскание местных форм колебаний отдельных стержней приводит при использовании этих методов к серьезным проблемам, поскольку в процессе расчета все собственные частоты и формы разыскиваются автоматически без какого-либо выбора. Это нужно принять во внимание в большинстве нагружений в реальных конструкциях. Следует заметить, что в большинстве случаев в реальных конструкциях эти местные вибрации ограничены связями, которые не принимаются в расчет в модели МКЭ, и их вклад в общее движение системы будет несущественным. Как правило, вклад масс таких местных вибраций очень мал. Использование точных методов в этом случае приведет немыслимым трудностям. Однако как приближенный основной метод редукции может значительно упростить вычислительный процесс.

Метод сопряженных градиентов с предобусловливателем (PCG)

Этот метод [9-13] пригоден для итерационных решателей. Применение этого метода рекомендуется для нахождения небольшого числа собственных частот и форм в многомерной задаче. Применение расчета псевдоформ (см. раздел 3.5) в сочетании с модифицированным методом Ланцоша или методом PCG_Ritz рекомендуется, если необходимо определить большое количество собственных форм и частот, например, в процессе сейсмического или спектрального расчета, и выбран итерационное решение.

Градиентный метод Ритца (PCG_Ritz)

Этот метод [8] доступен для итерационного решателя в при расчете в псевдо режиме. Это позволяет получить приближенное решение в виде векторов Ритца. Этот очень быстрый метод используется для сейсмического и спектрального расчета при решении пространственных задач (10 000 – 100 000 уравнений).

Модифицированный метод Ланцоша

Этот метод является дополнением к методу Ланцоша, расширяет его и применяется при использовании терационного решателя. Он работает также, как и метод Ланцоша в псевдорежиме. Однако отличается от метода Ланцоша, предназначенного для прямого решателя тем, что не требует факторизации матрицы жесткости. Вместо этого применяется основной градиентный метод с предобусловливателем. Такая процедура требует наибольшей затраты сил по сравнению с другими методами итерационного решателя, хотя часто оказывается и не самой быстрой.

Все динамические методы детально обсуждаются приложении 3A.

3.2. Типы матрицы масс

В процессе динамического расчета пользователь имеет дело с такими типами матрицами масс, как сосредоточенная без учета вращения, сосредоточенная с учетом вращения и Совместимая матрицы масс.

Сосредоточенная без учета вращения и сосредоточенная с учетом вращения – это диагональные матрицы масс. Эти матрицы требуют минимума вычислительных усилий.

Совместимая матрица масс - это заполненная матрица, которая появляется, когда пользователь рассматривает систему с распределенными параметрами. Принято считать, что распределенная матрица масс описывает инерционные свойства конструкции более точно, чем сосредоточенная матрица. В большинстве случаев сосредоточенная матрица масс требует хорошей аппроксимации, поскольку очевидно, что инерционные параметры могут быть представлены менее точно, чем параметры жесткости. Фактически, потенциальная энергия выражается через перемещения, в то время как кинетическая энергия есть функция производных от перемещений. Хорошо известно, что ошибка аппроксимации увеличивается при каждом дифференцировании [4]. Таким образом, для непрерывных объектов (твердое тело, плита, оболочка) при той же сетке можно аппроксимировать параметры масс менее точно, чем параметры жесткости.

Обычно в качестве функций формы для стержней используются полиномы Эрмита. Это точное решение для большинства статических и динамических задач, если рассматриваются сосредоточенные матрицы масс. Однако, точные решения динамических задач для стержня относятся к классу функций Крылова (специальные комбинации тригонометрических и гиперболических функций). В этом случае параметры жесткости представляются полиномами Эрмита с одновременным использованием совместимой матрицы масс. Следует заметить, что не существует ограничений на использование различных типов функций для статической и динамической задач. Поэтому в большинстве случаев нет преимущества в усложнении динамической модели путем использования распределенных масс по сравнению с точным решением для приближенной модели (сосредоточенные массы).

Кроме того, обычно собственные массы элементов стержневой конструкции (решетки, колонны и т. д.) пренебрежимо малы по сравнению с массами стен и кровли (постоянная нагрузка), которые учитываются в процессе приведения постоянных нагрузок к массам. Такие приведенные массы обычно и порождают эффект распределенных масс.

Все сказанное выше приводит к выводу, что для большинства встречающихся на практике случаев сосредоточенная матрица масс обеспечивает достаточную точность аппроксимации инерционных свойств конструкции. Следует запомнить, что совместимая матрица масс требует при решении задач относительно больших затрат времени вычислений, особенно, если решается задача высокого порядка. Перед выбором модели с распределенными массами нужно быть уверенным, что реализация такой модели действительно необходима.

Предполагается, что использование распределенной матрицы необходимо при расчете модели с жесткими связями.

Если используется прямой решатель "sparse" или итерационное решение, для вычисления произведения матрицы на вектор используется техника "элемент-за-элементом" (EBE). Это означает, что совместимая матрица масс никогда не собирается в ансамбль, а все операции осуществляются только на уровне элемента. Если используется решатель систем с профильным хранением матриц, то совместимая матрица масс собирается в ансамбль и хранится так же, как и матрица жесткости. Для небольших задач (самое большее ~3000 уравнений) техника "профильных матриц" оказывается более быстрой, хотя с увеличением размера задачи необходимое для расчета время растет чрезмерно.

Имеется возможность использовать дополнительные сосредоточенные массы и заменять массами статические нагрузки.

Если используются метод Ланцоша, модифицированный метод Ланцоша (итерационное решение) или метод PCG_Ritz , то могут решаться только задачи с заполненными матрицами масс.

3.3. Верхние пределы

Существует возможность определить все собственные числа и собственные формы, которые не превосходят заданного пользователем значения. Это значение рассматривается как верхний предел. Когда этот инструмент активен, то программа Robot ищет ω₁, ω₂, …, ω_n ≤ ω^*, где ω^* - верхний предел. Алгоритм решает задачу в два этапа. На первом этапе выполняется проверка условия Штурма: существует ли число "n" собственных значений, меньших, чем верхний предел. На следующем этапе алгоритм генерирует n собственных значений, каждое из которых не превышает значение верхнего предела.

Для тех вариантов расчета, которые используют значение верхнего предела, рекомендуются метод Ланцоша и метод BLSI, поскольку это необходимо для получения большого числа собственных значений.

Если активизирован верхний предел, то игнорируется критерий процента участия масс (см. раздел 3.4).

Например, такая проблема может появиться при работе с французскими сейсмическими нормами PS-92, в которых требуется, чтобы были учтены все частоты, меньшие, чем 33Гц.

3.4. Процент участия масс

Вклад массы в процентах для каждой формы (k=1; 2; …; N) определяется как

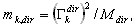
где 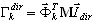, 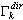— коэффициент участия масс для k-той собственной формы, I_dir является вектором единичной трансляции по направлению dir (напр: X, Y, Z), 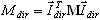- общая масса в направлении dir , 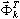является k-той собственной формой, .

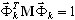Процент участия масс в направлении dir равен M%dir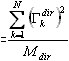. Коэффициент определяет вклад всех форм в движение конструкции в рассматриваемом направлении.

При выборе модального расчета и процент участия масс для заданного максимального числа узлов меньше, чем требуется, пользователь получает сообщение о неудовлетворительности процента участия масс, в то время как вычисления заканчиваются без внесения исправлений.

Для обеспечения автоматического поиска требуемых приведенных масс нужно использовать один из вариантов расчета - Сейсмический расчет или расчет Псевдоформы. Подробности представлены в разделе 3.5.

3.5. Определение собственных частот и форм

В данном разделе рассматриваются следующие варианты (режимы) динамического расчета: Модальный расчет, Сейсмический расчет и расчет Псевдоформы.

Некоторые сейсмические нормы (UBC-97, французские PS-92) требуют, чтобы сумма участия масс по каждому направлению (или только по горизонтальным направлениям) составляла не менее чем 90%. Может возникнуть несколько проблем, когда очень трудно достичь требуемой суммы участия масс за счет большого числа малых вкладов низших частот. Как правило, такая проблема возникает при местном характере низших частот. Для исправления ситуации при решении таких трудных задач предлагаются режимы сейсмического расчета и расчета псевдоформ. Неэффективность такого расчета иллюстрируется в приложении 3С. Для этих двух режимов расчета можно использовать метод Ланцоша для прямого решателя. Модифицированный метод Ланцоша и метод PCG_Ritz пригодны для решения задачи псевдоформ, когда выбран итерационное решение.

Модальный расчет

Этот тип динамического расчета составляет хорошо известный подход, представленный в предыдущих версиях программы Robot.

Доступные методы: BLSI, SI, Ланцоша и Основной метод редукции для прямого решателя и метод PCG для итерационного решателя.

Критерий сходимости для прямого решателя: итерации будут остановлены при 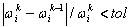, где i = 1, 2,..., N; k - номер итерации, n - число форм (задается пользователем). Основной метод редукции не осуществляет проверку сходимости, поскольку это не итерационный метод, хотя и представляет собой разновидность метода Ритца. Для достижения точности результата он требует увеличения числа степеней свободы.

Критерий сходимости для метода PCG (итерационное решение) включает:

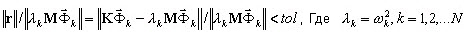
Подробности описаны в приложении 3A.

Верхний предел – это нижняя граница значения за период, частота и пульсация. Если этот параметр отличен от нуля, то будут рассчитаны все последовательные собственные пары - частота-форма от нуля до верхнего предела.

Масса % - процент участия масс (сумма вкладов масс для всех рассчитанных мод по каждому направлению).

Проверка по Штурму - это проверка пропущенных масс между 0 и параметром перемены знака и состоит в подсчете отрицательных элементов по главной диагонали разложенной матрицы жесткости .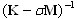

Для решения задачи высокого порядка эта процедура очень дорогая. Следует заметить, что при сейсмическом и спектральном расчете нет необходимости определять бесконечный спектр собственных значений. Важно только обеспечить достаточный процент вклада модальных масс по каждому направлению. Если это условие выполняется, то полнота базиса обеспечена. Заметим, что применение метода BLSI позволяет получить частичную проверку непрерывности спектра собственных значений без привлечения проверки по Штурму. Для дополнительной информации см. описание метода BLSI.

Число форм	Верхние пределы	Масса %	Действия программы
N	0 неактивно	0 неактивно	Проверка по Штурму проводилась. Отсутствуют пропущенные частоты для первых форм N. Она доступна для прямых решателей при использовании методов BLSI, SI или метода Ланцоша. Не доступна для основного метода редукции и для всех итерационных решателей. Определяет N первых последовательных собственных частот. Выполняется проверка по Штурму. Если определены пропущенные частоты, то пользователь получает сообщение о числе пропущенных частот. Возможны следующие варианты ответа на сообщение: Да - тогда итерационный процесс продолжается после того, как определены пропущенные собственные частоты; после этого снова проводится проверка по Штурму; Нет - тогда уже найденные частоты сохраняются в качестве окончательного результата, затем рассчитывается следующее нагружение; Отмена - тогда итерации будут продолжены до тех пор, пока не будут найдены все пропущенные частоты; предупреждение игнорируется. проверка по Штурму не выполнялась. проверка по Штурму не выполняется.
N	ω *	Неактивно (из-за активного верхнего предела)	Это возможно только при использовании прямых решателей и методов BLSI, SI, метода Ланцоша. Это недоступно при использовании основного метода редукции и всех итерационных решателей. Проверка по Штурму проводится в начале вычислений числа частот N1, между нулем и верхним пределом: 0 < ω1 < ω2 < … < ωN1 < ω* Если (N1 > N), то программа предупреждает о числе частот N1. Возможны следующие варианты ответа: да, что означает 0 < ω1 < ω2 < … < ωN1 < ω*; нет, что будет говорить о желании остановить вычисления. Если (N1 <= N), означает 0 < ω1 < ω2 < … < ωN1 < ω* без каких-либо замечаний. В обоих случаях можно получить число собственных пар, большее, чем N1, однако они будут сохранены как окончательный результат только в том случае, если выполняется условие: 0 < ω1 < ω2 < … < ωN1 < ω*. Все найденные частоты, большие ,чем ω*, будут потеряны.
N	Не активно (из-за активной из массы %)	Активно: 0 < масса % < =100%	Это доступно для всех прямых решателей. Не доступно для итерационных решателей. Если масса % неудовлетворительна, то появляется соответствующее предупреждение. Корректировка не проводится. Наоборот, вычисления продолжаются так же, как и в первом случае.

сейсмический;

Этот вариант расчета осуществляется только с помощью прямых решателей - решателz систем с матрицами профильного хранения либо разреженного решателя.

При сейсмическом и спектральном расчете наличие последовательно расположенных собственных частот не является важным, поскольку будут учитываться только те частоты и формы, которые вносят значительный вклад в сейсмический отклик, то есть имеют значительный коэффициент участия масс. Проверка по Штурму не выполняется.

Вообще, метод Ланцоша обычно обеспечивает сходимость большего числа собственных частот по сравнению с количеством N частот в порядке их последовательного увеличения. Если пользователь хочет восстановить пропущенные собственные значения, необходимо, чтобы число рассчитанных частот было значительно больше по сравнению с числом N нужных первых собственных частот. Например, обычно метод Ланцоша дает следующие сходящиеся частоты.

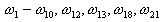
Если пользователю нужны частоты, расположенные в последовательном порядке, он получит только первые 10 частот. Последние 4 будут просто отброшены, как и соответствующие вклады масс. Основная задача сейсмического расчета - учесть все сходящиеся собственные значения, а не только последовательно идущие первые. Это обеспечивает большую сумму вклада масс по сравнению с модальным расчетом.

Доступные методы: метод Ланцоша.

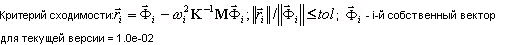
Верхние пределы игнорируются.

Вклад текущей массы определяется как среднее значение от вкладов M%x, M%y, M%z для пространственной задачи и как минимальное значение вкладов M%x, M%z для двумерной задачи (M%x, M%y, M%z - текущие суммы вклада масс по направлениям x, y, z соответственно). Эту стратегию можно объяснить тем, что обычно очень сложно задать достаточное процентное значение массы для вертикального направления. В окончательных результатах можно проверить вклад массы по каждому направлению.

Число форм	Верхние пределы	Масса %	Действия программы
N	Не активно	Не активно (0)	Вычисляется N непоследовательно расположенных частот. Проверка по Штурму не выполняется. Число полученных собственных частот всегда равно N.
N	Не активно	Активно 0 < масса % < = 100%	Показатель N игнорируется. Вычисления продолжаются, пока процент участия масс не станет меньше, чем требуемое значение процента участия масс - масса %, или если пользователь предупрежден соответствующим требованием прекратить вычисления, или если число найденных собственных чисел достигло максимального заданного значения. Это значение в данной версии программы принято равным 100. После каждых 20 шагов метода Ланцоша программа пересчитывает число полученных решений и изменяет текущий процент вклада масс. Пользователь получает сообщение о достигнутом значении вклада масс и может дать один из следующих ответов на это сообщение: да - продолжается вычисления для следующих 20 шагов метода Ланцоша и снова появляется сообщение, а если требуемое значение вклада масс вновь не достигнуто и число полученных решений не превосходит назначенного значения; нет - полученные решения сохраняются, как окончательный результат, и программа переходит к следующему варианту расчета; отмена - в будущем игнорируются все предупреждения и вычисления продолжаются.

Псевдоформы

В данном виде динамического расчета можно использовать как прямые, так итерационные решатели. Тип динамического расчета - расчет псевдоформ рекомендуется как для сейсмического, так и для спектрального расчета лишь в случае, когда модальный и сейсмический расчеты требуют слишком больших затрат времени. Модальный и сейсмический типы расчета используют собственные формы и частоты как базисные векторы для представления сейсмического отклика. Для обеспечения удовлетворительной суммы вклада масс в таких трудных задачах приходится определять большое число собственных частот и форм. Расчет Псевдоформ бракует эту идею и создает аппроксимацию Ритца для низших собственных частот с использованием векторов Ланцоша для прямого решателя или градиентного метода Ритца [8] и модифицированного метода Ланцоша для итерационного решателя. В большинстве случаев такой подход оказывается более эффективным, поскольку требуется меньшее число базисных векторов, чем в случае с модальным расчетом. Это было показано в работе E.L.Wilson [1-3]. Псевдоформы подобны векторам Ритца с весом, предложенным в работах [1-3] и реализованным в SAP2000. Следует заметить, что французские нормы PS-92 признают применение этого научно обоснованного метода для того, чтобы добавить несколько систем базисных векторов к существующим собственным формам для увеличения суммы вклада масс. Детали расчета псевдоформ и эффективность их использования показаны в приложениях 3B и 3C соответственно.

Верхние пределы игнорируются.

Вклад текущей массы определяется как среднее значение от вкладов M%x, M%y, M%z для пространственной задачи и как минимальное значение вкладов M%x, M%z для двумерной задачи (M%x, M%y, M%z - текущие суммы вклада масс по направлениям x, y, z соответственно). Эту стратегию можно объяснить тем, что обычно очень сложно задать достаточное процентное значение массы для вертикального направления. В окончательных результатах можно проверить вклад массы по каждому направлению.

Число форм	Верхние пределы	Масса %	Действия программы
N	не активно	не активно (0)	Возможно использование обоих прямых решателей и итерационного решателя. Генерируется N базисных векторов для определения рабочего подпространства. Сохраняется N базисных векторов для использования их в сейсмическом и спектральном расчетах. Этот режим рекомендуется.
N	Не активно	Активно 0 < масса % < = 100%	Доступно использование только прямых решателей. Генерируется N базисных векторов для определения рабочего подпространства. Сохраняются те базисные векторы, которые обеспечивают заданное значение процента участия масс - масса %. Число сохраненных базисных векторов меньше N, если масса % < 100%

3.6. Спектральный расчет

Спектральный метод отклика используется для сейсмических и спектральных расчетов. Главная идея этого метода состоит в декомпозиции конструкции с большим числом степеней свободы (MDOF) в систему осцилляторов с одной степенью свободы (SDOF). Затем программа рассчитывает отклик для каждого из этих независимых осцилляторов и осуществляет статистическое суммирование экстремальных откликов для каждого осциллятора с использованием методов SRSS, CQC, метода десяти процентов и метода двойных сумм [3, 21].

При применении модального или сейсмического расчета, эту систему SDOF осцилляторов определяют собственные формы и частоты. Когда используется расчет псевдоформ, то систему SDOF осцилляторов определяет набор базисных векторов псевдоформ (раздел 3.5).

Введение псевдоформ требует нового подхода к определению отклика для каждой формы. Классический подход состоит в следующем:

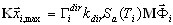( 3.1.1 )

где K, M - матрица жесткости и матрица масс, Γ - коэффициент участия масс, S_а - спектральное ускорение, T - период, I - номер формы, k - коэффициент шкалы спектра, dir - индекс направления сейсмического движения (dir = X, Y, Z), x - вектор перемещения для максимальной реакции i-ой формы.

Справедливо следующее отношение (см. приложение B):

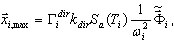( 3.1.2 )

где 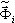обозначает базисный вектор ( 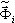не обязательно должно быть точной апроксимацией 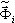- точного собственного вектора 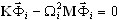, ω_i - апроксимация точного собственного значения Ωi. Можно показать, что (3.1.1) дает точно такое же решение 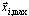, что и (3.1.2), если 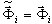(Ωi = Ωi). Однако, (3.1.2) применимо не только для прямых решателей, но и для итерационных решателей, поскольку этот метод не требует процедуры расщепления по отношению к матрице жесткости. Метод более быстрый, чем (3.1.1) и позволяет более надежно контролировать результаты (сумму сил - сумму реакций).

Приведенная ниже формула получается из (3.1.1)

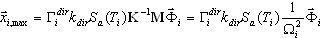( 3.1.3 )

Модальный вектор отклика 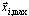описывает экстремальный отклик соответствующего осциллятора SDOF. Следующий шаг должен состоять в определении окончательного отклика MDOF конструкции с учетом статистического усреднения между формами и между направлениями сейсмических воздействий.

Программа Robot (более ранних версий) позволяет связать различные направления статистически независимых сейсмических воздействий с их собственной шкалой множителей для каждого варианта нагрузки. Статистическое усреднение направлений реализуется с использованием комбинаций опций "сумма абсолютных значений" и "квадратный корень из суммы квадратов" для каждой формы. Соответствующие опции определены в "Рабочих настройках".

Опция "сумма абсолютных значений" дает следующее:

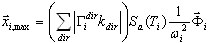( 3.1.4 )

Квадратный корень из сумма квадратов "делает усредняя части 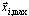соответствующих Сейсмическая ввода направления движения, как .

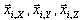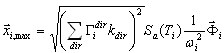( 3.1.5 )

Можно показать, что каждый компонент 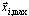представляет собой комбинациюs SRSS соответствующих компонентов ,

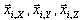где i =1,2,..., Н где i =1,2,…,N – номер формы или псевдоформы.

Комбинации SRSS или CQC мод или псевдо мод используются для получения окончательного отклика рассматриваемой MDOF конструкции после усреднения полученных модальных векторов отклика 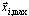i =1,2,…,N.

Модальные векторы усредненного отклика 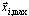, i =1,2,…,N это те же комбинации опций "сумма абсолютных значений" и "квадратный корень из суммы квадратов", как и в случае, когда отдельные направления сейсмических вкладов были определены для текущего варианта нагрузки (например, Kx=Kz=0, Ky=1).

Программа Robot (версия 12.2 и более поздние) сохраняют описанные выше процедуры усреднения модальных откликов по различным направлениям сейсмических вкладов, однако это не исключает использования более эффективных средств. Рекомендуется определять отдельные направления сейсмических вкладов для каждого варианта нагрузки, затем применять либо комбинации направлений SRSS (это соответствует Американскому сборнику правил), либо так называемые комбинации Ньюмарка(в соответствии с французскими сейсмическими нормами PS-92 с нормами Еврокод-8).

Проиллюстрируем новые возможности на следующем примере.

В этом случае (отдельное движение от сейсмического толчка для каждого варианта нагрузки) типичные значения коэффициентов шкалы равны:

Kx=1; Ky=Kz=0 для dir = X (нагружение S_X)

Kx=0; Ky=1; Kz=0 для dir = Y (нагружение S_Y)

Kx=Ky=0; Kz=0.7 для dir = Z (нагружение S_Z; интенсивность вертикального движения предполагается равной 2/3 интенсивности горизонтального)

Для каждого статистически независимого вклада в сейсмическое движение определяются три варианта нагружения. Модальные отклики для каждой формы будут теми же, что и в (3.1.2) (i = 1,2,…,N; dir = X,Y,Z ).

Далее необходимо определить среднее значение фактора по всем модам каждого направления сейсмического воздействия:

где 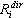- некоторый фактор (перемещение, усилие, напряжение для i-той формы, возникающее из-за движения от сейсмического толчка в направлении dir, которое соответствует модальному отклику 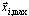(полученному из (3.1.2));

Rdir - результат SRSS или CQC комбинации рассматриваемых форм или псевдоформ.

Затем осуществляется усреднение всех активных направлений сейсмического толчка в соответствии с выбранными опциями.

комбинация SRSS:

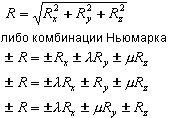
Опции спектрального расчета могут определить произвольный спектр движений от сейсмического толчка.

3.7. Сейсмический расчет

Спектральный метод отклика используется для сейсмических и спектральных расчетов. Сейсмический расчет осуществляется на основе Спектрального расчета (раздел 3.6), однако спектральные ускорения Sa = Sa(Ti) рассчитываются в соответствии с выбранным сейсмическим кодом, а не определяются пользователем, как это делается в Спектральном расчете.

В программе Robot (версии 12.0 и более поздние) доступны сейсмические нормы UBC-97. Спектральный расчет отклика осуществляется в соответствии с разделами 1631.5.1 – 1631.5.3 бельгийских норм UBC-97. Используя средства программы Robot, можно удовлетворить и требованиям раздела 1631.5.4 ("Упругие параметры отклика"). Основные компоненты сдвига Vx, Vy, Vz, компоненты изгибающих Mx и My и крутящего Mz моментов (ось OZ предполагается вертикальной) представлены в таблице "Реакции" в строке сумма сил, как для каждого модального отклика, так и для комбинаций мод по SRSS и CQC.

В программе доступны следующие сейсмические нормы:

• UBC97;
• PS 69 R. 82;
• AFPS;
• PS 92;
• RPA 88;
• DM 16.1.96;
• ЕС 8;
• IBC 2000;
• P100 92;
• турецкие нормы;
• китайский нормы;
• аргентинские нормы;
• EAK 2000.

3.8. Выборочные фильтры

Только те формы, которые имеют относительно большой процент участия масс, вносят заметный вклад в сейсмический отклик конструкции. Поэтому имеет смысл учитывать только такие формы. Остальные формы с малым процентом участия масс в процессе сейсмического расчета игнорируются. Число не учитываемых форм обычно значительно больше, чем число форм с большим процентом участия масс. Поэтому пространство жесткого диска и время вычислений существенно экономятся, если выбрать только формы с заметным фактором участия масс.

Используются два способа.

• Первый способ состоит в следующем. На основе результатов, полученных при проведении предварительного модального расчета, определяется предел массы - граничное значение вклада модальных масс.
• Все формы с вкладом модальных масс ниже, чем этот предел, игнорируются, и составляется список принятых форм по каждому направлению сейсмического воздействия (сейсмического нагружения).

Этот способ наиболее эффективен, хотя требует предварительного проведения модального расчета. Второй способ позволяет использовать фильтры в рамках программ спектрального и сейсмического расчета, однако эти фильтры занимают много места на диске и требуют больших вычислительных затрат.

Рассмотрим другой пример. Ниже представлены результаты модального расчета. Сейсмические варианты определены следующим способом: Dir_X (Kx=1; Ky=Kz=0), Dir_Y (Kx=0; Ky=1; Kz=0) и Dir_Z (Kx=Ky=0; Kz=1)

Таблица 1

Номер формы	участие масс UX (%)	участие масс UY (%)	участие масс UZ (%)	Точка
1	0,05	12,01	0,004	0,803
2	67,43	0,06	0,005	0,705
3	0,002	0,08	0,07	0,686
4	0,001	0,008	0,009	0,650
5	25,4	0,07	2,06	0,590
6	0,09	68,5	5,05	0,540
7	0,08	10,3	0,06	0,490
8	0,07	0,06	0,56	0,460
9	0,05	0,07	30,56	0,420
10	0,08	0,06	0,25	0,380
11	0,06	0,01	26,7	0,270

Предположим, что мы получаем все формы с процентом участия масс, большим, чем принятый предельный процент. Соответствующие значения участия масс даны в таблице. Заметим, что если направление сейсмического воздействия в варианте Seism_X принято равным ( 1 0 0), формы со значениями участия масс по направлениям UY и UZ вообще не дают вклада в сейсмический отклик (см. раздел 3.6):

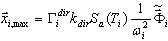
где dir = X, Y, Z - направление сейсмического воздействия; 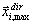- максимальный отклик для i -той формы; 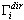- коэффициент участия масс; Sa(Ti) - спектральное ускорение; 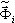- i-тый собственный вектор или в случае псевдоформы базисный вектор. Скалярный множитель в правой части приведенной выше формулы 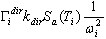определяет вклад i-той формы в сейсмический отклик по направлению dir. В этом случае, когда Ky = Kz = 0, значительные вклады дают формы 2 и 5. Остальные формы не дают вклада в сейсмический отклик из-за равенства нулю множителя Kdir (dir = Y, Z) и малого участия остальных масс по направлению dir=X. Можно показать таким же образом, что для варианта Dir_Y достаточно учесть формы 1, 6, 7, а для варианта Dir_Z – формы 5, 6, 9, 11.

Итак, при использовании фильтра программа учтет только форму 2 в случае воздействия по направлению Dir_X , форму 3 для варианта Dir_Y и форму 4 для варианта воздействия Dir_Z без существенной потери участия масс. Заметим, что если не использовать эти фильтры, можно будет достичь применения 11 форм по каждому нагружению.

Этот прием позволяет сократить время вычислений в случае решения задач большого порядка, а также уменьшить требования к свободному месту на диске и сократить количество данных, обрабатываемых постпроцессором. При этом потеря точности будет сравнима с потерей точности при использовании традиционных методов, которые не используют фильтров.

Например, задача большого порядка PJG203 содержит 34 266 уравнений с шириной ленты после оптимизации равной 990. Соответствующая модель МКЭ представлена в приложении 3D – см. рис. A1. Было получено 25 собственных пар для распределенной матрицы масс и рассчитано 3 варианта сейсмической нагрузки. Время расчета на Pentium PRO (64 МБ оперативной памяти, 200МГц) составило приблизительно 50 часов. Потребовалось более 1ГБ памяти на жестком диске. Более того, возникла проблема с модулем проектирования стальных конструкций, вызванная недостаточным свободным местом на диске. (для расчета сочетаний SRSS и CQC пришлось иметь дело с определением 25 форм при трех вариантах сейсмического нагружения для задачи с большим числом степеней свободы и соответственно с большим числом значений перемещений, внутренних усилий и напряжений). Применение фильтров позволило успешно решить эту задачу.

3.9. Гармонический расчет

Вводится следующее определение реакции конструкции на гармоническую нагрузку:

F(t) = F sin( ωt) ,

где w - пульсация возмущающей нагрузки. Поведение конструкции описывается как

(K - ω² M) X = F,

где X - амплитуда вектора перемещения.

3.10. Расчет колебаний

В программе Robot реализован метод модальной декомпозиции (суперпозиции). Он основан на представлении движения конструкции в виде суперпозиции движений не связанных форм. Поэтому метод требует предварительного определения собственных значений и собственных частот. Для этой цели рекомендуется метод Ланцоша. Метод разложения по формам использует разделенные сокращенные уравнения. Метод модальной декомпозиции использует преимущество несвязанных уравнений. Этот подход удобен при расчете динамического отклика конструкции, подверженной долговременному воздействию динамической нагрузки (например, нестационарное нагружение, вызванное действием оборудования или сейсмическим воздействием). Математические основы и подробности приложения представлены в работах [3; 4; 6].

Уравнение без учета затухания принимает следующую форму:

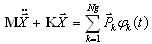(3.11.1)

где Ng - число "групп нагрузок", φ_k(t) - отдельная временная фаза для k-ой группы нагрузок.

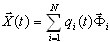(3.11.2)

где 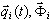- соответственно i-тая нормальная координата и форма (собственный вектор Ритца). Подставляя (3.11.2) в (3.11.1) и добавляя слагаемые демпфирования, получаем следующие несвязанные модальные уравнения [3; 4; 6]

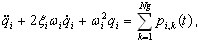(3.11.3)

где 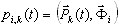, ξi - модальный параметр демпфирования (обычно ξi = 0,05 – 0,2; при ξi = 1, означает критическое демпфирование – границу между колебательным движением и непериодическим процессом), ωi - круговая частота вибраций (пульсация), i = 1; 2; ...; N

Каждое уравнение решается численно. Применяется метод второго порядка с автоматическим выбором шага интегрирования. Результирующий вектор перемещений для определенных моментов времени t = t1, t2, …, t5 получается при подстановке qi(t5) в (3.11.2).

Для расчета сейсмического отклика можно применить метод модальной декомпозиции. В этом случае уравнения движения принимают следующую форму

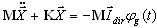
и соответственно несвязанные уравнения форм принимают вид

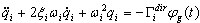(3.11.5)

где 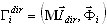- коэффициент участия масс для i-той формы и направление dir сейсмического воздействия. Каждая форма должна быть нормализована таким образом: 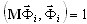. В заключение все результаты (перемещения, скорости, ускорения, внутренние силы, реакции и т. д.) сохраняются только для определенных моментов времени t = t1, t2, ..., t5. Быстродействующий постпроцессор позволяет получить результаты динамического процесса как в виде графика, так и в табличной форме. На графиках представляются выбранные факторы (перемещение, скорость, ускорение, реакции, поперечные силы, изгибающие моменты и т. д.) для выбранных степеней свободы и представляется вид деформированной конструкции в отдельные моменты времени. Таблицы позволяют не только видеть соответствующие значения, но и сохранять автоматически максимальное и минимальное значения факторов отклика среди полученных для всех моментов времени.

3.11. Модальный расчет, учитывающий статические нагрузки

В данном разделе рассматриваются малые линейные вибрации относительно статического положения равновесия, вызванные приложенной статической нагрузкой. Известно, что статические силы влияют на частоты свободных колебаний. Обычный модальный расчет не учитывает это влияние, однако существует вариант модального расчета, учитывающий статические силы.

Полные нелинейные уравнения движения относительно положения статического равновесия системы при действии статических нагрузок имеют вид:

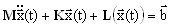(3.12.1)

where M, K - матрица масс и матрица жесткости, L(x(t)) - нелинейный оператор, x(t), b - вектор перемещения и вектор нагрузки. Процедура линеаризации уравнений состоит в следующем

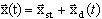(3.12.2)

where x_st является частью общего решения, которое описывает положение статического равновесия и x_d (t) - вектором малых динамических перемещений. Нелинейный оператор может быть представлен в виде разложения в ряд Тейлора

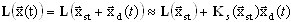(3.12.3)

где 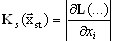матрица напряжение-жесткость, которая представляет собой Якобиан и учитывает действие статических сил. Таким образом, получаем:

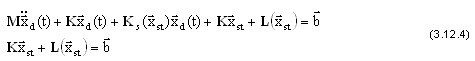
Первое выражение есть результат линеаризации малого динамического перемещения (заметим, что если 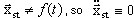), а второе выражение описывает положение нелинейного статического равновесия. Поэтому малое динамическое движение относительно положения статического равновесия запишется так:

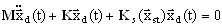(3.12.5)

Подставим x_d (t) = Φ e^{i ω t}. Задача собственных значений взята из (3.12.5)

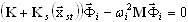(3.12.6)

где ω_i - собственное значение; Φ_i - собственный вектор.

Расчет выполняется в два этапа:

1. Линейный (3.12.7) или нелинейный (3.12.8) расчет статического напряженно-деформированного состояния, возникающего при действии статической нагрузки:

   K x_st = b (3.12.7)

   K x_st + L(x_st ) = b, (3.11.8)

   где x_st - неизвестный вектор статического состояния, b - вектор приложенных статических сил (вектор статической нагрузки), K - матрица жесткости, L (x_st , b) - нелинейный оператор. Вектор статической нагрузки b может быть результатом сочетания нескольких статических нагрузок. Следует заметить, что линейное решение не удовлетворяет точно нелинейным уравнениям равновесия (3.11.8). Так, вектор x_st состояния статического равновесия является результатом приближенного решения, и матрица жесткости-напряжения K_s(x_st) содержит ошибку. Если рассматриваемая конструкция является достаточно жесткой, то нелинейные эффекты в ней проявляются незначительно и такая аппроксимация представляется корректной. В противном случае необходимо решить нелинейную статическую задачу (3.11.8) (которую технически невозможно осуществить вручную). Очевидно, линейное решение (3.2.17) является более быстрым по сравнению с нелинейным (3.11.8). При нелинейном решении имеет место K_s(x_st ) = G (x_st )= G, где Gгеометрическая матрица жесткости.

2. Расчет собственных значений (3.12.6)

   Положительные значения ωi (ωi > 0), как известно, представляют положение устойчивого равновесия, отрицательные значения (ωi < 0) - положение неустойчивого равновесия, значение (ωi =0) соответствует потере устойчивости (продольному изгибу).

   Отсутствие положительной определенности матрицы K + K_s(x_st ) означает, что статическая нагрузка достигает критического значения. Появляется предупреждающее сообщение о том, что в процессе решения нелинейной статической задачи отсутствует сходимость(3.11.8). Рекомендуется прервать вычисления, поскольку дальнейшие вычисления бессмысленны.

   Для конструкций, содержащих канаты и элементы, работающие на растяжение-сжатие, имеет смысл только нелинейный расчет.

Рассмотрим пример, показанный на приведенном ниже рисунке.

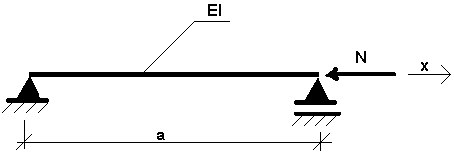
Рис. 3.11.1

Пусть N - статическая нагрузка. Поведение такой конструкции описывает следующее уравнение:

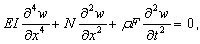( 3.11.9 )

где: w - перемещение при изгибе, ρ - плотность материала, F - площадь поперечного сечения.

Решение разыскивается в форме

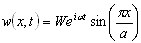( 3.11.10 )

После подстановки (3.11.10) в (3.11.9) получаем:

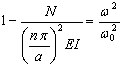, ( 3.11.11 )

где 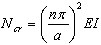- критическая нагрузка, ω₀ - собственное значение при n = 0 (результат при обычном модальном расчете). И в заключение получаем

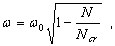( 3.11.12 )

где ω - собственное значение для конструкции, подверженной воздействию статической нагрузки . Результат представлен графически на рис. 3.11.2:

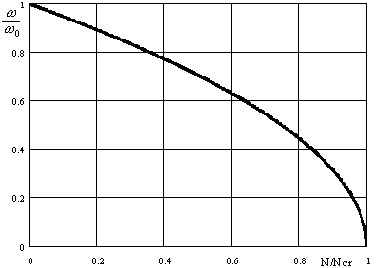
Рис. 3.11.2

Зависимость ω = ω (λ), где λ - параметр нагружения, в случае реальной конструкции оказывается более сложной по сравнению с представленной выражением ( 3.11.12 ) [ 1,22 ].

Приложение 3A

Методы решения задачи собственных значений

Следует понимать, что не существует "лучшего универсального метода" решения задачи собственных значений

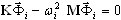, i =1; 2; …; n ( A1 )

где K - матрица жесткости, M - матрица масс, собственная форма и ω_i - пульсация. Для большинства задач такой метод требует меньших ресурсов (времени вычислений и свободной памяти на жестком диске) по сравнению с другими методами. Однако это не исключает иной ситуации при решении других задач. Тогда рекомендуется использование иного метода. Существующая версия Robot поддерживает различные методы решения обобщенной задачи собственных значений (A1). Каждый из методов имеет свои преимущества и недостатки. Ниже мы даем несколько рекомендаций по выбору метода расчета. Надеемся, что в большинстве случаев они наилучшим способом приведут к требуемым результатам.

Метод итераций в подпространствах (SI) реализуется точно так, как описано в [4], поэтому описание этого метода здесь не приведено.

По Ланцошу

Метод Ланцоша [12;16;17] - мощный трудоемкий метод, используемый для решения задач собственных значений высокого порядка (A1). Его можно применять, когда для решения задачи выбраны прямые решатели (решатель систем с матрицами профильного хранения или разреженный).

Этот подход позволяет определять n-ое количество требуемых собственных значений и форм с заданной точностью. Чем большее количество собственных пар нужно определить, тем более заметными оказываются преимущества метода Ланцоша. Однако применение метода имеет некоторые ограничения.

Трехдиагональная матрица T не подлежит декомпозиции. Это означает, что невозможно будет рассчитать конструкцию, которая состоит из двух или трех несвязанных подконструкций. В таком случае либо каждую конструкцию следует рассматривать отдельно, либо нужно применить другой метод расчета, например, метод блочной итерации в подпространствах (BLSI) или основной метод редукции.

Матрица масс М должна иметь быть либо сосредоточенной с вращениями, либо совместимой.

Недопустима нулевая плотность.

Метод Ланцоша использует приведение к трехдиагональной матрице T .

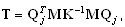, ( A2 )

где Q_j = {q1, q2, …, qj} - прямоугольная матрица с элементами Neq x j, и Neq - число уравнений, j - номер шага по Ланцошу, qj - j-ый вектор Ланцоша. Выражение

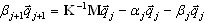( A3 )

генерирует следующий вектор Ланцоша qj+1 и определяет текущую строку матрицы T

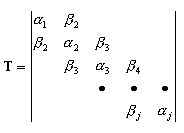
Таким образом, получаем задачу собственных значений:

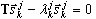, k = 1; 2; …; j ( A4 )

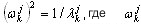- j-ая апроксимация круговой частоты ω_k, k = 1; 2; …; n, где n — требуемое число собственных пар. Алгоритм продолжает вычисления (при увеличении j - номера шага процедуры Ланцоша) до тех пор, пока не будет достигнута требуемая точность по всем требуемым собственным значениям.

Процедура выборочной ортогонализации поддерживает требуемый уровень ортогонализации векторов Ланцоша qj, что обеспечивает надежность и устойчивость численного процесса расчета. Мы используем экономичные методы для реализации процедуры выборочной ортогонализации и для решения редуцированной задачи собственных значений (A4) путем применения двойных QR-итераций со сдвигами.

Исходные собственные векторы определяются по формуле

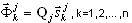( A5 )

Подробности по методу можно найти в работах [12,16,17].

Основной метод редукции

Основной метод редукции [4; 5] известен как модифицированный метод Рэлея-Ритца [4]. В работе [5] этот метод представлен как дискретный вариант метода Бубнова-Галеркина. Этот алгоритм используется для получения приближенных значений для нескольких первых собственных пар, если имеется какая-либо информация о них. Для получения редуцированной системы метод требует задания основных степеней свободы (MDOF). То есть, можно контролировать процесс создания редуцированной модели. Это является мощным средством для того, кто имеет опыт динамического расчета конструкций и рассчитывает конструкцию такого типа, свойства которого уже известны. Этот метод позволяет исключить ненужные степени свободы (DOF) из редуцированной модели и преобразовать первоначально сложную исходную задачу с большим числом степеней свободы к редуцированному виду со сравнительно малым числом степеней свободы Это достигается со значительно меньшим числом степеней свободы. Опыт проведения динамического расчета показывает, что этим методом можно решить некоторые задачи, которые при использовании автоматических методов редукции (методов BLSI, SI и метод Ланцоша) требуют очень сложных вычислительных процессов. Например, отыскание местных форм колебаний отдельных стержней приводит при использовании этих методов к серьезным проблемам, поскольку в процессе расчета все собственные частоты и формы разыскиваются автоматически без какого-либо выбора. Это нужно принять во внимание в большинстве нагружений в реальных конструкциях. Следует заметить, что в большинстве случаев в реальных конструкциях эти местные вибрации ограничены связями, которые не принимаются в расчет в модели МКЭ, и их вклад в общее движение системы будет несущественным. Как правило, вклад масс таких местных вибраций очень мал. Использование точных методов в этом случае приведет немыслимым трудностям. в то время как использование приближенного основного метода редукции может значительно упростить вычислительный процесс.

Метод имеет следующие ограничения.

Пользователь должен сам определить основные степени свободы: основные узлы и основные направления. Предполагается, что в качестве основных степеней свооды можно определять только перемещения, но не углы поворота.

Алгоритм пригоден для любых типов матриц масс, однако в отношении времени вычислений наиболее предпочтительны сосредоточенные без вращений, чем матрицы масс.

• Последовательная проверка по Штурма недоступна. Существует единственный метод проверки сходимости. Увеличивается число основных степеней свободы (путем введения дополнительных основных узлов и основных направлений), повторно решается задача и сравниваются величины собственных значений с величинами, полученными ранее.

Такой метод преобразует задачу собственных значений по МКЭ, имеющую первоначально высокий порядок

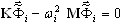(A6)

модель (A1) в задачу собственных значений для преобразованной модели

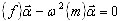(A7)

где {f} - матрица влияния, {m} - обобщенная матрица масс для преобразованной модели

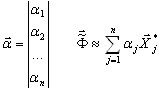(A8)

где n - число степеней свободы преобразованной модели. Основой этого преобразования является статическое решение, зависящее от соответствующих единичных состояний: узловые единичные силы прикладываются соответственно в каждой основной точке в выбранном основном направлении. Статическая задача высокого порядка решается для n правых частей:

i = 1, 2, …, n (A9)

где Ti - вектор нагрузки, который соответствует i - той единичной силе Пользователь может определить основные узлы и основные направления. Все требуемые операции осуществляются программой

Редуцированная задача собственных значений решается методом Якоби, который приводит к приближенным значениям частот ω_i, и форм 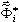, i =1; 2; …; n. Подробности по данному методу представлены в работе [5].

Блочный метод итераций в подпространствах

Блочный метод итераций в подпространствах (BLSI) предназначен для решения обобщенной задачи собственных значений (A1). Он доступен для прямых решателей: решателя систем с матрицами профильного хранения либо разреженного решателя. Это мощный трудоемкий подход. Его использование настоятельно рекомендуется при решении задач высокого порядка, когда нужно получить большое число собственных значений (более 10). Метод BLSI можно использовать при расчеты отдельных конструкций. При модальном расчете доступны матрицы всех типов (сосредоточенная без вращений, сорсредоточенная с вращением и совместимая). Область применения этого подхода ограничена модальным расчетом. Сейсмический расчет и расчет псевдоформ доступны лишь тогда, когда выбран метод Ланцоша.

Последовательная проверка по Штурму используется для обнаружения пропущенных степеней свободы. Метод BLSI контролирует непрерывную сходимость собственных значений. Отсутствие непрерывной сходимости собственных значений свидетельствует о наличии пропущенных частот. Однако непрерывная сходимость собственных значений не обеспечивает абсолютную уверенность в том, что нет пропущенных собственных частот. Тем не менее, опыт численных расчетов показывает, что в большинстве случаев последовательная проверка по Штурму не обнаруживает пропущенные частоты, если метод BLSI обеспечивает непрерывную сходимость решения. Итак, большим преимуществом этого метода состоит в возможности обойти требующую больших затрат процедуру проверки Штурма, если нет необходимости полной гарантии отсутствия пропущенных собственных частот. Если непрерывность сходимости собственных значений отсутствует, то появляется следующее сообщение (Рис.А1).

Основная идея метода BLSI [1-3] состоит в проведении итераций совместного вектора в подпространстве фиксированного размера. Каждый сходящийся вектор перемещается из рабочего подпространства (блока) и вместо него добавляется новый исходный вектор. Ортогональность сходящихся векторов обеспечивается на каждом шаге итерации.

Если в процессе модального расчета наблюдается медленная сходимость, то рекомендуется применять процедуры ускорения сдвига [1; 4].

, ( A10 )

где K_σ= K - σ M, σ - величина сдвига. В начале расчета полагается, что σ = 0. Обновление величины параметра сдвига делается автоматически, если после определенного числа контрольных шагов итерации не появляются новые сходящиеся собственные значения. Например, пусть контрольное число шагов итерации назначено равным пяти. Затем после четырех итераций появляется пять новых сходящихся собственных значений. Значение смещения σ = 0. После следующей итерации появилось три новых сходящихся собственных числа. Значение смещения σ = 0. Затем после пяти итераций не появились новые сходящиеся собственные значения. Алгоритм обнаруживает слабую сходимость, принимает σ = ω₈ ², обновляет K_σ = K - σ M и факторизует обновленную и смещенную матрицу K_σ. Затем после двух итераций появляются два новых сходящихся собственных значения. Величина сдвига остается равной ω₈ ². Затем после пяти итераций новые собственные значения не появляются. алгоритм фиксирует "слабую сходимость" и принимает ω₁₀ ², обновляет K_σ = K - σ M и факторизует обновленную и смещенную матрицу K_σ.

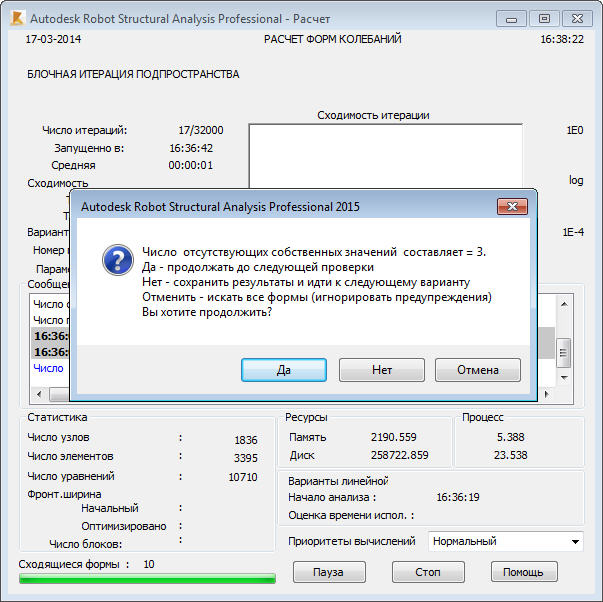
Рис. A1. В процессе работы метода BLSI программа обнаруживает отсутствие непрерывной сходимости собственных значений.

Возможные варианты ответа на предупреждение:

• Да - вычисления будут продолжены, пока не появится следующее сходящееся собственное значение; после этого будет сделана следующая проверка;
• Нет - результаты будут сохранены и начнется расчет следующего нагружения;
• Отмена - вычисления продолжаются, пока не обеспечивается полностью непрерывная сходимость собственных значений. Предупреждение игнорируется.

Здесь представлены не все рекомендации. Можно применять, а можно и не применять ускорения сходимости. Следует помнить, что применение соответствующего сдвига - наиболее сильное средство ускорения сходимости. С другой стороны, факторизация измененной матрицы K_σможет потребовать большой затраты времени, особенно для задачи высокого порядка. Таким образом, окончательное решение о применении ускорения сдвига пользователь принимает на основании опыта и интуиции.

Пользу ускорения сдвига иллюстрирует следующий пример. На рис. А2 показана расчетная схема. Имеется 50 собственных форм, полученных методом BLSI. Выбран прямой решатель систем с профильным хранением матриц (skyline). Принимается точность 1,0e – 09. Сходимость, начиная с 38 формы, оказалась настолько медленной, что за 20 минут не появилось никакого результата. Когда была активизирована процедура ускорения сдвига (изменение сдвига было назначено через каждые 5 неуспешных шагов итерации), то время вычислений для всего расчета сократилось до 50 секунд. Хотя можно привести примеры вычислений, при которых применение сдвига понижает число итераций, но увеличивает время вычислений. Мы рекомендуем активизацию процедуры ускорения сдвига, когда обыкновенный расчет (процедура сдвига выключена) на некоторых этапах работы BLSI приводит к большому числу итераций.

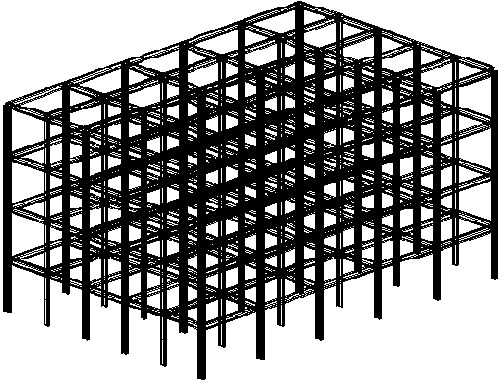
Рис.A2. Пространственная рама

Модифицированный метод Ланцоша

Этот метод представляет собой видоизменение метода Ланцоша в расчете псевдоформ для итерационного решателя. Обычный метод Ланцоша требует факторизации матрицы жесткости (см. приложение A3). Когда встречается задача высокого порядка, то факторизация матрицы жесткости требует большой затраты времени.матрицей. В случае задач высокого порядка (свыше 100 000 уравнений) обычно значительных вычислительных усилий требует не только факторизация матрицы жесткости, но и решение системы уравнений с факторизованной матрицей.

Модифицированный метод Ланцоша базируется на итерационной процедуре. Он позволяет избежать хранения, составления и факторизации матрицы жесткости высокого порядка. Оценка каждого вектора Ланцоша требует приблизительно таких же вычислительных затрат, как при решении статической задачи с одной правой частью. Что касается расчета псевдоформ, то он понижает требуемое число векторов Ланцоша по сравнению с модальным расчетом, который применяется при использовании модифицированного метода Ланцоша.

Для генерирования векторов Ланцоша применяется итерационное решение AEBEIS [7; 8]. Рекомендуется использование технологии ICCF (неполная факторизация Холецкого) для обоих уровней агрегационного предусловливания [7,8,18-20] и для обычного предусловливания (не многоуровневого). Это обеспечивает быстрые операции при определении произведения матрица-вектор и быстрое решение соответствующего предусловливания. Заметим, что допуск, принятый для итерационного решателя (Рабочие настройки / Расчет конструкций / Параметры), определяет точность получения векторов Ланцоша. Обычно достаточно принять ее равной 1,0e – 04. Можно учесть тем большее количество форм, чем меньшее число векторов Ритца будет в соответствующих собственных формах и чем полнее представлена сумма модальных масс.

Метод сопряженных градиентов с предобусловливателем (PCG)

Метод PCG [9-13] рекомендуется для определения малого числа собственных форм в модальном расчете при использовании итерационного решателя. Он может быть с успехом применен при расчете на ветровую нагрузку и для проверки нескольких низших форм, полученных методом PCG_Ritz. Доступны все виды предобусловливания (Инструменты / Рабочие настройки / Итерационные / Параметры), определенные для статического расчета. Могут использовать все типы масс (

Метод сопряженных градиентов с предобусловливателем основан на прямой минимизации отношения Рэлея

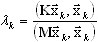(A11)

с использованием градиентного метода, где: k - число итерации λ_k - соответствующая апроксимация собственных значений. Градиентный метод разыскивает такое значение параметра α_k, которое обеспечивает минимальное значение для λk (A11):

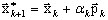(A12)

где p_k - вектор сопряженного направления. Поиск соответствующего значения α_k [см. 9-13] приводит к соотношению:

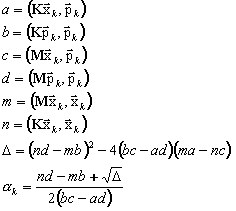
Предобусловивание B применяется для ускорения сходимости

B z_k+1 = r_k+1 -> z_k+1 (A13)

Направление градиента определяется как

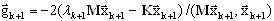(A14)

Новое сопряженное направление определяется таким образом

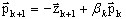(A15)

где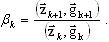

Итерации выполняются до тех пор, пока

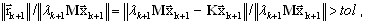(A16)

где tol - принятая точность. Обычно tol = 1,0e – 02 обеспечивает достаточную в инженерных целях точность. Нужно помнить, что отношение сходимости (A16) вычисляется по очень строгой норме (раздел, касающийся точности вычислений). Точность, принятая выше, предусматривает точность собственных значений не хуже, чем 1,0e – 04.

Если достигнута сходимость первой собственной пары, то эта пара сохраняется как окончательный результат и итерации начинают разыскивать следующую собственную пару. Для исключения дублирования собственных пар на каждом шаге итерации применяется процедура ортогонализации предварительно определенных собственных векторов. Этот процесс повторяется, пока не будут определены все желаемые собственные пары.

Наиболее эффективный путь ускорения сходимости по методу PCG - это реализация хорошего предобусловливания. Все типы предобусловливания, имеющиеся для итерационного решателя, доступны для метода PCG. Настоятельно рекомендуется применять многоуровневое предобусловливание [18-20] или не многоуровневое предобусловливание со сглаживанием ICCF [9-12] из решателя AEBEIS [7,8].

Градиентный метод Ритца (PCG_Ritz)

Метод PCG_Ritz [8] - это быстрый метод определения системы векторов Ритца при расчете псевдоформ с использованием итерационного решателя. Такой подход может быть очень эффективным при сейсмическом и спектральном расчете пространственных конструкций с 10 000 – 60 000 уравнений.

Метод основан на построении ортогональной системы базисных векторов. Для минимизации отношения Рэлея на каждом шаге подготовки базисного вектора применяется градиентный метод с многоуровневым агрегированным предобусловливанием на базе техники "элемент-за-элементом". Он обеспечивает сходимость базисного вектора к наименьшему собственному значению без агрегации и декомпозиции матрицы жесткости большого размера. Этот метод зачастую более эффективен для расчета динамического отклика по сравнению с классическим модальным методом суперпозиции, это особенно касается расчета сейсмического отклика. Предлагаемый метод позволяет использовать произвольный тип конечных элементов благодаря агрегационному подходу и обеспечивает быстрое решение и невысокие требования к памяти на жестком диске благодаря использованию техники EBE. Этот метод очень эффективен при решении задач с совместимыми матрицами жесткости.

Задача собственных значений формулируется так:

Kφ - λM φ = 0 (A17)

где K, M - соответственно матрица жесткости и матрица масс, φ - собственный вектор и λ - собственное значение. Будет показана процедура развития системы базисных векторов x0, x1, …, xn к самой низкой собственной форме. Для минимизации отношения Рэлея используется градиентный метод с предобусловливанием

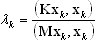(A18)

где 0 ≤ k ≤ n, k - это номер шага развития; n+1 - количество базисных векторов, которое определяет размер подпространства, принадлежащего (x0, x1, …, xn); n+1 << N, где N - это количество степеней свободы в рассматриваемой задаче (A17). Очень часто рассматриваемая задача собственных значений оказывается плохо обусловленной. Этом случае сходимость базисного вектора xk к нижнему значению очень медленная. Для исправления этой ситуации применяется оператор предобусловливания B. Выражение B z_k = r_k -> z_k означает решение данной системы уравнений соответствующего вектора zk, где B - оператор предобусловливания и r_k = Kx _k - λ_k M x_k - соответствующий остаточный вектор.

Базисные векторы удовлетворяют следующим условиям ортогональности:

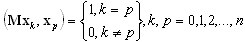(A19)

Задача собственных значений, имевшая первоначально высокий порядок (A17), преобразована к собственной задаче подпространства меньшего порядка.

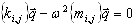(A20)

Матрицы проекции подпространства определяются как {k_ij} = {Kx_i, x_j} и {m_ij} = {Mx_i, x_j} = U, где U - единичная матрица.

Векторы Ритца v₁, v₂, …, v_n+1 для производных базисных векторов x0, x1, …, xn и соответствующие аппроксимации частот ω₁, ω₂, …, ω_n+1 используются для суперпозиции динамического отклика конструкции.

Процедура развития базисных векторов x_k, k = 0, 1, …, n к низшей собственной форме ограничена соответствующим шагом градиентного итерационного метода с предобусловливанием при решении задачи собственных значений. Хорошо известно, что сходимость итерационного метода с предобусловливанием существенно зависит от свойств оператора предобусловливания B. Этот оператор должен быть положительно определен, что допускает экономное решение B z_k+1 = r_k+1 позволяет лучшим образом удовлетворить ряду условий C ( B^-1 K) -> 1.

Последнее требование в случае градиентного метода Ритца обеспечивает хорошее приближение для нижних собственных частот и форм.

Этот метод доступен только для многоуровневого итерационного расчета, который обеспечивает хорошее качество предобусловливания. Используются обе технологии - технология предобусловливания EBE ("элемент-за-элементом") и технология ICCF. Качество полученных таким образом векторов Ритца существенно зависит от свойств оператора предобусловливания B (см. A13 и [8]). Если модель крупного уровня хорошо аппроксимирует собственные частоты, то векторы Ритца на тонком уровне дают хорошую аппроксимацию соответствующих собственных векторов [8]. Таким образом, качество результата, полученного таким методом, существенно зависит от способности модели крупного уровня обеспечить подобие заданной модели МКЭ (так называемый тонкий уровень). Обычно один уровень агрегации обеспечивает хорошую аппроксимацию. Если число уровней агрегации более одного, то качество результата не гарантируется. Это основное ограничение применения метода для решения задач высокого порядка, когда число уравнений превышает ~60 000.

Если матрица предобусловливания B = K(крупный и тонкий уровни совпадают), предлагаемый градиентный метод Ритца превращается в метод Ланцоша [8]. Математическая основа метода изложена в работе [8].

Модальный расчет. Точность вычислений

Обобщенная задача собственных значений определяется следующим образом:

Kφ - λM φ = 0 (A17)

где K, M - соответственно матрица жесткости и матрица масс, {φ, λ} - собственные пары (форма и собственное значение). Определяются два типа остаточных векторов:

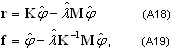
где {φ, λ} обозначают вычисленные собственные пары, которые включают определенные ошибки вычислений. Первое выражение задает остаточный вектор в терминах сил, второе – в терминах перемещений.

Применяются четыре различных критерия оценки ошибок вычислений для собственных векторов:

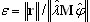• . Это очень жесткий критерий. Обычно ε ≤ 0,01 означает, что первые четыре знака в величине собственного значения определены точно. Критерий используется только в методе PCG, когда выбран итерационное решение.
• e = (r, φ). Это относительно мягкий критерий по сравнению с предыдущим. Он применяется при методе Ланцоша, когда выбран итерационное решение.
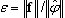• . Это мягкий критерий, поскольку сходимость перемещений в данной реализации МКЭ более быстрая по сравнению со сходимостью внутренних усилий. Критерий используется в методах BLSI, SI и методе Ланцоша, если выбраны прямые решатели: решатель систем с матрицами профильного хранения либо разреженный решатель.
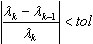• ·, где λk, λk-1 - два последовательных собственных значения на k-ом, k-1-ом шаге итерации, а tol означает допуск, заданный в диалоговом окне "Параметры модального расчета". Критерий используется при определении форм методами BLSI, SI и методе Ланцоша, если выбраны прямые решатели (решатель систем с матрицами профильного хранения или разреженный). Этот критерий не трудоемкий и очень быстрый. Использование критерия (4) позволяет сократить время вычислений методами BLSI, SI и методом Ланцоша, особенно при решении задач высокого порядка. Когда завершен расчет собственных значений, критерий (3) используется как окончательная проверка точности. Значение 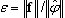пользователь увидит в таблице в колонке "Точность". Если точность по отдельной форме оказалась недостаточной, то необходимо повторить расчет собственных значений с менее жестким критерием точности собственных значений tol.

Рассмотренные выше соображения суммирует следующая таблица. Символ N/A означает, что соответствующая проверка сходимости не проведена. Результаты окончательной проверки получают один раз и их можно посмотреть в таблице в колонке "Точность". Проверка сходимости проверяется постоянно в процессе вычислений.

	Прямые решатели		Итерационное решение
Тип критерия	BLSI, SI, метод Ланцоша	Основной метод редукции	Модифицированный метод Ланцоша	PCG_Ritz	PCG
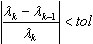
В процессе вычислений		Не применимо	Не применимо	Не применимо
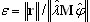
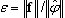
Окончательная проверка		Не применимо	e = (r, j)	Не применимо

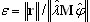
Заметим, что при использовании метода Ланцоша для определения сейсмических мод проводится проверка сходимости 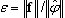через каждые 20 шагов Ланцоша. Основной метод редукции и метод PCG_Ritz - это разновидности метода Ритца. Поскольку не используется итерационный процесс, то проверка точности не осуществляется.

Если точность каких-либо форм после вычислений оказывается недостаточной, то необходимо сделать следующее:

Прямые решатели		Итерационное решение
BLSI, SI, Метод Ланцоша - определение форм	Метод редукции базиса	Модифицированный метод Ланцоша	PCG_Ritz	PCG
Уменьшение числа tol в диалоговом окне "Параметры модального расчета"	Увеличение числа базисных узлов и базисных направлений	Увеличение числа форм; уменьшение числа tol в диалоговом окне "Параметры итерационного решателя"	Увеличение числа форм; уменьшение числа уровней агрегаций; увеличение числа внутренних итераций	Уменьшение значения tol в диалоговом окне "Параметры модального расчета"

Приложение 3B

Расчет псевдоформ

Исходные уравнения движения при сейсмических воздействиях имеют вид:

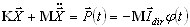(B1)

K, M - матрицы жесткости и масс;

I dir - направление единичного вектора; φ(t) - фаза ускорения основания

Решение разыскивается в форме:

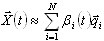(B2)

где q_i - базисные векторы размера Neq - число уравнений в первоначальной схеме по МКЭ.

Эти векторы должны удовлетворять следующим требованиям:

• кинематические и статические граничные условия;
• линейная независимость;
• полнота базиса.

Для решения можно применить либо вектора Ланцоша, либо некоторые вектора, полученные для единичной сосредоточенной узловой силы (основной метод редукции для прямых решателей или градиентный метод Ритца - PCG_Ritz).

Проекция подпространства описывается так:

Заметим, что β имеет размер N; матрица Q имеет размер Neqx.

Уравнения подпространства (B3) будут решаться с использованием декомпозиции собственных векторов (в подпространстве, которое определяется соотношением Q = {q1, q2,..., qN}).

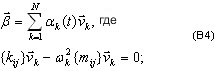
Заметим, что декомпозиция (4) - это точное выражение, так как индекс k предполагает значения от 1 до N – по полному размеру подпространства Q.

Подстановка (B4) в (B3) приводит к несвязанной системе уравнений

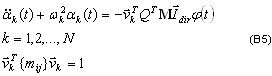
Рассмотрим

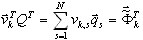(B6)

Таким образом, (B5) может быть представлено в виде

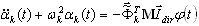(B7)

где k=1,2,…,N.

Применим спектральный метод отклика к несвязанной системе уравнений

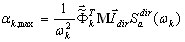(B8)

где 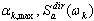- максимальный отклик для к-той формы подпространства спектральная функция ускорения соответственно.

Подставим (B8) в (B4) и затем в (B2):

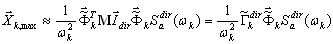(B9)

Заметим, что для N -> Neq:

ω_k -> Ω_k

где Ωk, 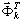- это точная собственная пара исходной собственной задачи по МКЭ

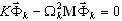(B10)

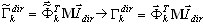и , где 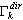— фактор участия масс для к-той собственной формы.

Заключение

1. Предлагаемый подход не требует "хорошей" аппроксимации , ω_k -> Ω_k. Допускается, чтобы 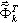, ω_k аппроксимировали 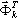, Ω_k с произвольной точностью.
2. Предлагаемый подход не хуже хорошо известного метода декомпозиции (суперпозиции). Оба эти метода образуют частные варианты метода проекций и сходятся к точному решению, если N - > Neq. (Это утверждение не вполне справедливо для спектрального метода отклика, поскольку этот метод имеет статистический характер и его сходимость к точному значению имеет место, когда N - > ∞. Очевидно, что для N > Neq возникнет вычислительный конфликт из-за того факта, что число базисных векторов не может превысить значение Neq. Поэтому можно получить различные решения для различных базисных векторов, когда N = Neq. Это особенность спектрального метода отклика. Для методов, отличающихся от спектрального метода отклика, полная сходимость имеет место, когда N = Neq. Сходимость при использовании спектрального метода отклика рассматривается только в статистическом смысле, потому что этот метод представляет собой статистический подход, стремящийся получить среднее решение в случае, когда отсутствует функция динамического процесса. Вследствие этого термин "точное решение" используется с осторожностью).
3. Какой из базисов лучше: векторы Ритца или собственные векторы? Лучшей считается система базисных векторов, которая обеспечивает лучшую сходимость к "точному" (N = Neq) при меньшем числе базисных функций N. Вопрос будет решен путем рассмотрения практических примеров.

   Обычно первая часть пары 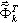, ω_k обеспечивает хорошую аппроксимацию соответствующей собственной пары 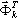, Ω_k (точность каждой пары можно определить в столбце "Точность" списка вывода). Только последняя пара 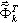, ω_K дает плохие аппроксимации точной собственной пары и может рассматриваться как псевдоформа (с точки зрения французских сейсмических норм PS-92).

4. Использование полного подпространства Q = {q1, q2,..., qN} обеспечивает быстрое увеличение участия массы. при модальном и сейсмическом расчете используется лишь часть этого подпространства.

Приложение 3C

Примеры использования сейсмического расчета и расчета псевдоформ

Очевидно, что существует много видов сейсмических и спектральных задач, в которых тяжело добиться удовлетворительного участия масс (70%- 90%). Можно решить так называемые "хорошие" задачи, используя хорошо известные методы.

• Пользователь назначает приблизительно число N первых форм
• и вычисляет первые последовательные N формы, используя модальный расчет.

Однако для "жестких" задач такой подход может оказаться недостижимым. Рассмотрим, например, задачи "Coreal" или "Museum". Это схемы по МКЭ, которые исследовались французскими инженерами. В таблице представлены полученные значения участия масс для различного числа определенных собственных форм. Для решения задач использовался модальный расчет (метод Ланцоша).

Журнал сходимости для задачи Coreal

Число сходящихся форм	Масса %
44	< 1%
62	12%
75	38%
89	60%
116	74%
154	77%
179	80%

Журнал сходимости для задачи Museum

Число сходящихся форм	Масса %
41	20%
106	40%
119	42%

Например, участие массы 80% означает, что для двух направлений сумма масс не меньше, чем заданное число. Модальный расчет определяет собственные формы, пока не будет достигнуто назначенное участие масс или не будет превзойден верхний предел числа форм. Окончательное решение по методу спектрального отклика получено в форме статистической суперпозиции собственных векторов.

При решении обеих задач число степеней свободы было меньше, чем 2000. Такие задачи считаются небольшими (по количеству числа степеней свободы). При решении пространственных задач и при решении задач высокого порядка оба метода - модальный и сейсмический расчет - могут оказаться на практике неприменимыми из-за громоздкости вычислительного процесса. В таких случаях рекомендуется использовать расчет псевдоформ. Ниже в таблице представлен журнал сходимости в решениях задач "Coreal" и "Museum".

Журнал сходимости в задаче "Coreal"

Количество базисных векторов	Масса %
10	58%
20	67%
40	70%
80	80%

Журнал сходимости в задаче "Museum"

Количество базисных векторов	Масса %
10	60%
20	66%
40	71%

Прим.: Чтобы получить 80 собственных векторов при модальном расчете, необходимо определить примерно 130 – 150 векторов Ланцоша. Вычислительные затраты при расчете псевдоформ оказываются значительно меньшими (примерно в3-5 раз).

Сходимость результатов при расчете псевдоформ иллюстрируется на следующем примере. В таблице представлены результирующие сочетания максимальных и минимальных значений CQC при модального расчете и при расчете псевдоформ.

Форма	Ux (см)	Uy (см)	UZ (см)	Процент массы
Модальный	5,52002e – 00	5. 88293e – 00	5,83013e – 00	81%
Псевдо, Nvect = 10	5,58710e – 00	5. 89055e – 00	5,00224e – 00	80%
Псевдо, Nvect = 20	5,52937e – 00	5,88870e – 00	6,08661e – 00	91%

Nvect - количество базисных векторов.

Приложение 3D

Примеры применения методов модального расчета к решению задач высокого порядка

Пример 1

Сравнение времени вычислений по методу BLSI и по методу Ланцоша. Рассматривается различное число собственных форм.

В качестве решателя использовался прямой решатель для разреженных матриц. Тип матрицы: сосредоточенная с вращениями.

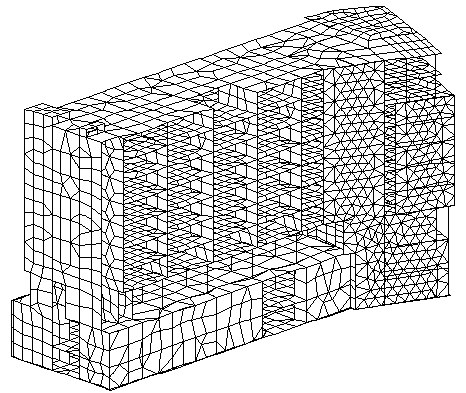
Рис. D1. Модель гостиницы. Количество узлов: 6 359; количество элементов: 7 264; количество уравнений: 37 806.

Таблица D1. Сравнение результатов

BLSI		По Ланцошу
f (Гц)	Точность	F (Гц)	Точность
2,794e – 001	1,082e – 006	2,794e – 001	5,680e – 015
1,388e + 000	1,389e – 004	1,388e + 000	2,199e – 013
1,520e + 000	7,847e – 004	1,520e + 000	8,193e – 012
1,644e + 000	2,469e – 004	1,644e + 000	4,497e – 013
1,747e + 000	2,691e – 004	1,747e + 000	5,455e – 014
1,776e + 000	3,092e – 004	1,776e + 000	9,127e – 013
1,806e + 000	3,153e – 004	1,806e + 000	6,621e – 013
1,818e + 000	6,383e – 004	1,818e + 000	3,656e – 012
2,622e + 000	1,565e – 003	2,343e + 000	2,047e – 011
2,634e + 000	1,383e – 003	2,622e + 000	1,223e – 005

Поскольку проверка по Штурму не выполняется, то при использовании метода BLSI между 8^-ой и 9^-ой формами появляется пропущенная собственная пара.

Таблица D2. Продолжительность времени расчета форм (в секундах)

Метод	10 форм	50 форм	100 форм
BLSI	735	6029	23572
По Ланцошу	1472	12637	25271

Факторизация матриц: 841 s.

Использование дополнительных методов (BLSI и Ланцоша) на базе мощного прямого решателя для разреженных матриц позволило в короткое время не только получить факторизованную матрицу, но и определить большое число собственных форм. Вычисления были проведены на компьютере P-350 (256 МБ ОЗУ).

Пример 2

Иллюстрирует применение различных методов к решению задачи PJG203. Модель содержит жесткие связи, которые приводят к использованию совместимой матрицы масс. Было определено 25 псевдоформ. 25 псевдоформ извлечены.

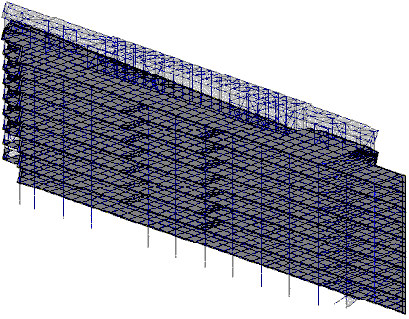
Рис. D2. Задача PJG203. Количество узлов: 5 945; количество элементов: 11 471; количество жестких связей: 22; количество совместимых узлов: 302; количество уравнений: 34 266.

Таблица D3. Время расчета, память на диске, первые 10 частот и соответствующая точность по разным методам.

Метод	Время (с)	HDD (МБ)	Частоты (Гц)	Точность
Решатель систем с матрицами профильного хранения	61 633	597	1,175e + 000 1,337e + 000 1,454e + 000 2,445e + 000 2,445e + 000 2,628e + 000 2,829e + 000 3,033e + 000 3,209e + 000 3,595e + 000	8,043e – 015 1,025e – 013 1,031e – 013 1,712e – 006 5,566e – 006 6,331e – 008 3,538e – 001 3,052e – 005 9,086e – 005 4,498e – 003
Разреженный	4 435	99	1,175e + 000 1,337e + 000 1,454e + 000 2,445e + 000 2,445e + 000 2,628e + 000 2,825e + 000 3,033e + 000 3,209e + 000 3,595e + 000	3,522e – 012 2,689e – 011 1,159e – 010 1,735e – 006 5,639e – 006 6,419e – 008 3,520e – 001 3,034e – 005 9,938e – 005 4,386e – 003
Модиф. По Ланцошу	3 459	24	1,175e + 000 1,337e + 000 1,454e + 000 2,445e + 000 2,445e + 000 2,628e + 000 2,791e + 000 3,033e + 000 3,209e + 000 3,595e + 000	3,719e – 004 3,891e – 004 6,601e – 004 1,454e – 003 1,875e – 003 2,946e – 003 3,364e – 003 3,923e – 003 2,175e – 002 1,580e – 001
PCG_Ritz	1 521	24	1,266e + 000 1,35e + 000 1,467e + 000 2,445e + 000 2,446e + 000 2,446e + 000 2,805e + 000 3,035e + 000 3,381e + 000 3,566e + 000	N/A - PCG_Ritz не является итерационным методом в отличие от метода Ритца. Поэтому вместо точных собственных форм получаются псевдо формы.

Для модифицированного метода Ланцоша были использованы следующие параметры: итерационное решение AEBEIS (многоуровневый вариант); предобусловливание ICCF; 2 уровня агрегации; 4 внутренние итерации, tol = 1,0e – 04 – точность определения векторов Ланцоша.

Для метода PCG_Ritz были использованы следующие параметры: итерационный многоуровневый решатель AEBEIS; предобусловливание ICCF; 1 уровень агрегации; 4 внутренние итерации.

Сходящиеся частоты изображены красным. Если точность (Приложение 3А) относительной нормы остаточного вектора для данной формы меньше, чем 5,0e – 02, то такая норма может рассматриваться как полностью сходящаяся к соответствующему собственному вектору. Поэтому частоты, изображенные красным, рассматриваются как точные значения для данной дискретной модели. Оценка ошибки по методу PCG_Ritz представлена в таблице D4. Можно заключить, что результаты, полученные по методу PCG_Ritz, обеспечивают достаточную для инженерных целей точность и такой подход можно использовать для быстрой оценки поведения конструкции при сейсмическом воздействии.

Дополнительные методы позволяют значительно снизить время расчета и уменьшают требования к памяти диска без каких-либо серьезных потерь корректности результатов.

Таблица D4. Оценка ошибки по методу PCG_Ritz

"точная" частота	результаты по PCG_Ritz	Ошибка (%)
1,175e + 000	1,266e + 000	7,7
1,337e + 000	1,350e + 000	1,0
1,454e + 000	1,467e + 000	0,9
2,445e + 000	2,445e + 000	0,0
2,445e + 000	2,446e + 000	0,0
2,628e + 000	2,446e + 000	7,0
2,791e + 000	2,805e + 000	0,5
3,033e + 000	3,035e + 000	0,1
3,209e + 000	3,381e + 000	5,4
3,595e + 000	3,566e + 000	0,8

Расчеты были выполнены на компьютере PC-450 (128 Мбайт ОЗУ).

Пример 3

Рассматривается заделанная по контуру тонкая квадратная плита с "совместимой" матрицей масс. Используется четырехузловой элемент оболочки и сетка 128x128 (число уравнений Neq = 99 072). Определено 40 псевдоформ.

В таблице D5 представлено время вычислений и размер памяти на диске при использовании метода Ланцоша с прямыми решателями (решателя систем с матрицами профильного хранения либо разреженного решателя), модифицированного метода Ланцоша (с итерационным решателем) и градиентного метода Ритца (PCG_Ritz).

Таблица D5. Время вычислений и объем памяти на жестком диске, требуемые по различным методам.

Метод	Время (с)	HDD (МБ)
Ланцош, решатель систем с матрицами профильного хранения	141 559	7 367
Ланцош, разреженный решатель	15 615	157
Модифицированный метод Ланцоша, итерационное решение	18 978	0 - в ядре
PSG_Ritz	9 651	192

Расчеты были выполнены на компьютере PC-450 (128 МБ ОЗУ).

Первые 10 частот, полученные методом Ланцоша при использовании прямых решателей (решателя систем с матрицами профильного хранения либо разреженного решателя) и модифицированным методом Ланцоша (с параметрами расчета - итерационное решение, предобусловливание ICCF, 3 уровня агрегации, 8 внутренних итераций, толерантность tol = 1,0e – 03) идентичны. Так как точность вычислений была очень высокой, то можно было считать полученные для заданной дискретной модели значения. Они приняты за эталонные значения оценки ошибки для частот, полученных по методу PCG_Ritz. Когда применялся метод PCG_Ritz, был выбран многоуровневый метод с предобусловливанием ICCF (один уровень агрегации, 4 итерации). Соответствующие результаты отображаются в таблице D6.

Таблица D6. Сравнение частот, определенных методом Ланцоша и методом PCG_Ritz

Частоты по Ланцошу (Гц)	Точность	Частоты по PCG_Ritz (Гц)	Ошибка (%)
3,722e + 000	5,918e – 014	3,725e + 000	0,08
9,112e + 000	4,474e – 014	9,115e + 000	0,03
2,282e + 001	2,424e – 012	2,284e + 001	0,09
2,915e + 001	5,866e – 013	2,915e + 001	0,00
3,315e + 001	1,795e – 013	3,318e + 001	0,09
5,801e + 001	2,373e – 011	5,803e + 001	0,03
6,565e + 001	3,028e – 011	6,571e + 001	0,09
6,873e + 001	6.907e – 014	6,875e + 001	0,03
7,602e + 001	1,549e – 012	7,609e + 001	0,09
9,949e + 001	3,302e – 013	9,953e + 001	0,04

Пример 4

Большое сооружение представлено на рис. D3

Рис. D3. Большое сооружение Количество узлов: 26 126, количество элементов: 30 272,

количество уравнений: 155 920.

Учитывается линейный статический расчет (один вариант нагружения) и определение 10 собственных частот. Для итерационного решения было принято tol = 1,0e – 04. Использовался метод Ланцоша с прямым решателем систем с матрицами профильного хранения. С прямым разреженным решателем использовались как метод Ланцоша, так и метод BLSI. Модифицированный метод Ланцоша использовался с итерационной процедурой (многоуровневый метод с тремя уровнями агрегации, 4 итерации, предобусловливание ICCF). Тип матрицы масс: сосредоточенная с вращениями.

Таблица D7. Время расчета и память на жестком диске по различным методам

Метод	Место на диске (МБ)	Линейная статика (один rhs) (с)	Определение 10 собственных форм (с)	Общее время (с)
Решатель систем с матрицами профильного хранения	5 702	136 065	65 052	203 878
AEBEIS	52	2 442	25 793	28 355
Разреженный (метод Ланцоша)	773	10 253	24 500	35 762
Разреженный NS (метод BLSI)	773	10 253	11 534	22 604

Расчеты проведены на компьютере PC-450 (128 МБ ОЗУ).

Заключение

Прикладные методы: BLSI, Ланцоша на базе прямого разреженного решателя и высоко производительного итерационного решателя AEBEIS с предобусловливателем ICCF представляют собой мощные средства для решения статической задачи и задачи собственных значений высокого порядка. Они существенно сокращают время расчета и требования к объему памяти на жестком диске по сравнению с традиционным решателем систем с матрицами профильного хранения Градиентный метод Ритца - PCG_Ritz - это оперативный подход, позволяющий оценить поведение заданной конструкции при сейсмическом воздействии. Если применяется один уровень агрегации, то соответствующие результаты, полученные методом PCG_Ritz, смыкаются с результатами, полученными методами Ланцоша и BLSI.

Список литературы

1. E.L.Wilson. An eigensolution strategy for large systems. Computers&Structures, Vol.16, № 1-4, pp.259-265, 1983.
2. Wilson. A new method of dynamic analysis for linear and nonlinear systems. Finite Elements in Analysis and Design, 1, 1985, 21-23, North-Holland.
3. E.L.Wilson, Three dimensional dynamic analysis of structures, Computers and Structures, Inc., Berkeley, California, USA, 1996.
4. R.W.Clough, J.Penzien. Dynamics of Structures. McGraw-Hill Book Comp., 1975, 634 p.
5. Фиалко С. Ю. Исследование влияния начальной погиби на частоты собственных колебаний ребристых конических оболочек, Прикладная механика, 1982.-т. 18.-№ П.-С. 118-122. (на русском языке)
6. Фиалко С. Ю. Nonsteady vibrations of ribbed conical shells under the influence of local loads, Soviet Applied Mechanics, 1987, v23, N6, p. 547-552.
7. Fialko S.Yu. High-performance aggregation element-by-element iterative solver for large-scale complex shell structure problems. Archives of Civil Engineering, XLV, 2, 1999. P.193-207.
8. Fialko S.Yu. High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis. CAMES (Computer assisted mechanics - engineering sciences), IV, 2000
9. Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrices, J. Comp. Physics", 74: 41 - 60, 1988.
10. Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Physics",81: 53 - 69, 1989.
11. Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Мет. Прилож. Мех. Eng., 62: 195 - 207, 1987.
12. Papadrakakis, Solving large -scale problems in mechanics, John Wiley & Sons Ltd., 1993.
13. S.Bitzarakis, M.Papadrakakis, A.Kotsopulos. Parallel solution techniques in computational structural mechanics. Comp. Methods Appl. Mech. Engrg. 1997, 148, p.75-104.
14. Hughes T.J.R., Ferencz M. Implicit solution of large-scale contact and impact problems employing an EBE preconditioned iterative solver, IMPACT 87 Int. Conference on Effects of Fast Transient Loading in the Context of Structural Mechanics, Lausanne, Switzerland, August 26-27, 1987.
15. Hughes T.J.R., R.M.Ferencz, and j.O.Hallquist. Large-scale vectorized implicit calculations in solid mechanics on a CRAY X-MP/48 utilizing EBE preconditioned conjugate gradients, Comput. Meths. Appl. Mech. Engrg., 61
16. Hughes Th. J. R. "The Finite Element Method. Linear Static and Dynamic. FEM Analysis."
17. Parlett B.N., 1980. "The Symmetric Eigenvalue Problem". Prentice-Hall, Inc., Englewood Cliffs, N.J. 07632.
18. Bulgakov, V.E., Belyi, M.E., Mathisen, K.M. Multilevel aggregation method for solving large-scale generalized eigenvalue problems in structural dynamics, Int. j. Numer. Methods Eng., 40: 453 - 471, 1997.
19. Bulgakov, V.E. Iterative aggregation technique for large-scale finite element analysis of mechanical systems, Comput. Struct, 52: N4, 829-840, 1994.
20. Bulgakov, V.E., G. Kuhn. High-performance multilevel iterative aggregation solver for large finite-element structural analysis problems, Int. j. Numer. Methods Eng., 38: 3529-3544, 1995.
21. Regulatory Guide
22. I.Ja.Amiro, V.A.Zarucky, V.N.Revutsky, Yu.V.Skosarenko, A.I.Telalov, S.Yu.Fialko. Колебания ребристых оболочек вращения, Киев, Наукова думка, 1988 г., 169 стр. (на русском языке).
23. S.Yu.Filako. Natural Vibration Modes of Ribbed Conical Shells, Soviet Applied Mechanics, 1984, v20, N11, p. 1033-1037. (на английском языке)