将通过麦克斯韦等式从数学角度说明感应加热的电磁现象。
不同形式的麦克斯韦等式可以改写成:
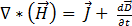 (利用安培定律)[1]
(利用安培定律)[1]
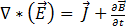 (利用法拉第定律)[2]
(利用法拉第定律)[2]
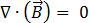 (利用高斯定律)[3]
(利用高斯定律)[3]
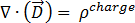 (利用高斯定律)[4]
(利用高斯定律)[4]
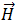 是磁场强度,
是磁场强度, 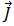 是传导电流密度,
是传导电流密度, 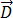 是电通量密度,
是电通量密度, 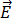 是电场,
是电场, 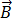 是磁通量密度,
是磁通量密度, 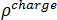 是电荷密度,
是电荷密度, 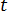 是时间。
是时间。
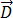 和
和 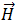 可以按照以下等式并,利用电磁材料属性介电常数
可以按照以下等式并,利用电磁材料属性介电常数  和磁导率
和磁导率 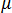 与
与 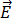 和
和 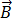 关联:
关联:
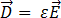 [5]
[5]
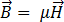 [6]
[6]
麦克斯韦等式可以利用欧姆定律进一步简化:
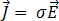 [7]
[7]
将等式 [5] 和 [7] 代入等式 [1] 中,注意电流频率小于 10 MHz,感生电流 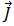 大于位移电流密度
大于位移电流密度 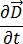 ,因此可忽略此项,则等式 [1] 可以改写成:
,因此可忽略此项,则等式 [1] 可以改写成:
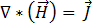 [8]
[8]
由于磁通量密度 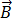 满足等式 [3] 中的零散度,因此可将其表达为磁矢量势
满足等式 [3] 中的零散度,因此可将其表达为磁矢量势 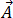 ,例如:
,例如:
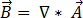 [9]
[9]
将等式 [9] 代入等式 [2] 中,即得出以下等式:
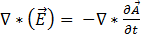 [10]
[10]
因此,
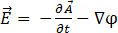 [11]
[11]
其中 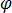 是电标势。等式 [7] 现变为:
是电标势。等式 [7] 现变为:
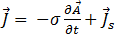 [12]
[12]
其中 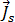 是线圈中的源电流密度的振幅,由以下等式得出:
是线圈中的源电流密度的振幅,由以下等式得出:
 [13]
[13]
将等式 [6]、[9] 和 [12] 代入等式 [8] 中得出:
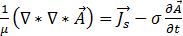 [14]
[14]
现在,将三重积矢量确定等式 [15]
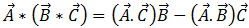 [15]
[15]
应用于等式 [14] 得出:
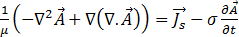 [16]
[16]
现在注意,对于一个分向量势场
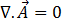 [17]
[17]
则等式 [16] 简化成
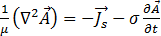 [18]
[18]
对于角频率 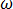 = 2
= 2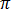 f 的正弦稳态,且单位 (rad/s),等式 [18] 变为:
f 的正弦稳态,且单位 (rad/s),等式 [18] 变为:
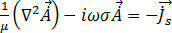 [19]
[19]
时间谐波磁矢量势 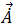 解出后,磁场磁通量密度可以利用等式 [9] 得出。导体中的时间谐波感应涡流
解出后,磁场磁通量密度可以利用等式 [9] 得出。导体中的时间谐波感应涡流 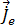 由等式 [20] 给出:
由等式 [20] 给出:
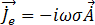 [20]
[20]
可从该等式中得出导体中的焦耳热 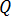 :
:
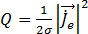 [21]
[21]
焦耳热是体积热源(单位:W/m3),由导体中的涡流感应产生。
感应加热中发生的传热现象是导体内的热传导,通过用于所有模拟的瞬态热传导方程表示。
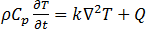 [22]
[22]
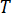 为温度,
为温度, 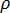 为密度,
为密度, 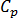 为比热容,
为比热容, 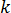 为材料的热导率,
为材料的热导率, 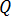 为等式 [21] 中的焦耳热。
为等式 [21] 中的焦耳热。